P I
R L
R Q
R I
R E
100
Solve
3x-5leq-4
xleq frac{1}{3}
100
True or False
f(x)=frac{ax+b}{cx+d}
The above function always has vertical and horizontal asymptotes whenever the values a, b, c and d are not zeros.
TRUE
100
True or False
The reciprocal of a quadratic always features horizontal and vertical asymptotes
FALSE
For the reciprocal of a function like
f(x)=x^2+3
there are no vertical asymptotes
100
True or False
A rational inequality with 2 x-intercepts and 2 vertical asymptotes will create 4 intervals on the x-axis so long as there are no x-intercepts and vertical asymptotes in common.
FALSE
This will create 5 intervals
100
This is one way in which solving rational equations is different from solving polynomial equations
We have to consider vertical asymptotes (there may be more, we will check all answers)
200
True or False
These are equivalent
-2x+7> 2
x-frac{7}{2}<-1
TRUE
When we multiply or divide by a negative, the direction of the inequality switches.
In this example, we divided by -2 both sides
200
True or False
If a linear function has a negative y-intercept and a negative slope, its reciprocal is always increasing.
TRUE
Increasing and Decreasing behaviours are always opposite. A linear with negative slope is always decreasing.
200
True or False
Whenever the quadratic function is increasing, the reciprocal is positive
FALSE
A reciprocal of a quadratic can be negative and decreasing
200
The solution intervals for the inequality
frac{2x^2+5x-3}{x^2-4}geq0
contain one or more errors. Find it (them)
Solution intervals:
(-infty,3]U[-2,1/2]U[2,infty)
There are vertical asymptotes at -2 and 2, so any solution that includes them is incorrect.
In the first interval it should read -3, not 3
200
The first step to solve this equation is...
frac{2x^2-6x+3}{x-6}=0
Multiply both sides by the denominator
300
True or False
To solve a polynomial inequality, we do not need to look at the asymptotes, only the x-intercepts
True
Polynomial inequalities do not feature asymptotes 😉
300
Equation of the reciprocal to the function shown here
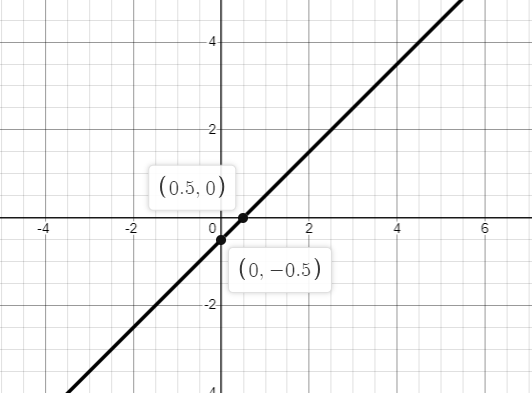
g(x)=\frac{1}{x-\frac{1}{2}}
300
True or False
The signs of a quadratic and its reciprocal are opposite
FALSE
Signs are always the same
300
Solve
frac{x+2}{x^2-16}leq0
{x<-4}U{-2leqx<4}
(-infty,-4)U[-2,4)
300
Solve
(2x^2-6x+3}/{x-6}=0
This is not factorable, you need quadratic formula
x= 0.634 and x = 2.366
400
Solve
x^3+2x^2-3x+5>5
(-3,0) U (1,+infty)
{-3<x<0}U{x>1}
400
Equation for the function shown below
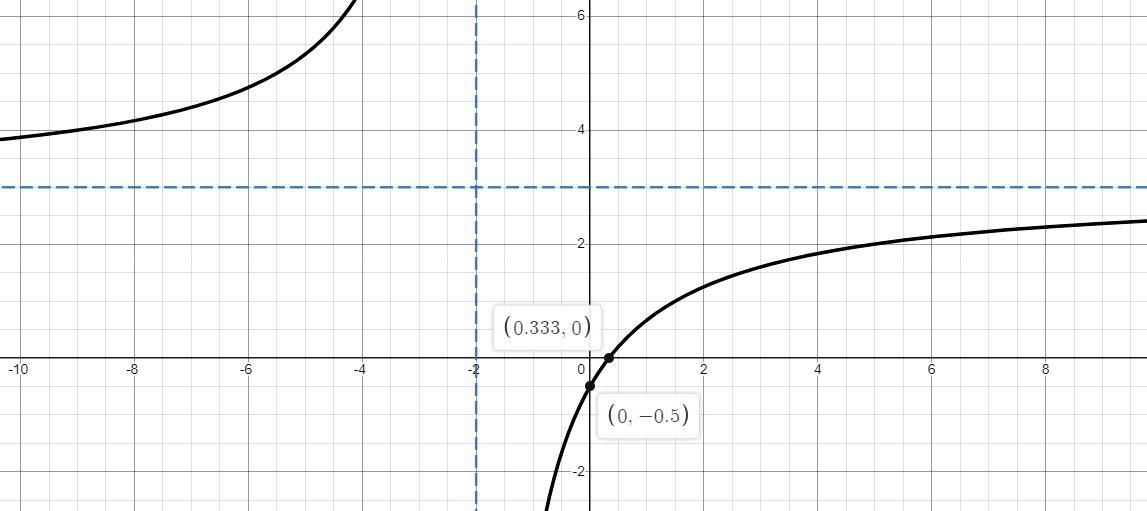
f(x)=\frac{3x-1}{x+2}
400
The equation of the reciprocal of the quadratic with the following characteristics:
x-intercepts at -5 and -2
It opens down
|a| = 3
g(x)=-\frac{1}{3(x+2)(x+5)
400
Solve
frac{2x-1}{5x+3}geq0
(-infty,-3/5)U[1/2,+infty)
{x<-3/5}U{xgeq 1/2}
400
Solve
frac{x^2-3x-18}{x^2-x-6}=0
x = -3 and x = 6
500
Solve
2x^3-3x^2-23x+17<5
(-infty,-3)U(frac{1}{2},4)
{x<-3}U{frac{1}{2}<x<4}
500
Equation of the function with the following characteristics
x-intercept at -0.4
y-intercept at -frac{2}{3}
vertical asymptote at frac{3}{2
horizontal asymptote at 2.5
g(x)=\frac{5x+2}{2x-3}
500
Create an example of a reciprocal of a quadratic function that has no vertical asymptote and a horizontal asymptote at 3
Many possibilities, here is a simple one
f(x)=frac{1}{x^2+2x+4}+3
500
Solve
frac{2x^2+x-1}{x^2-4x-4}leq0
Interval Solutions
[-1, -0,83) U [0.5, 4.83)
500
Solve
frac{x-3}{10}=4x
x=-1/13