Permutations
Combinations
Vocabulary
Mutually Exclusive
Conditional Probability
100
If five digits 1, 2, 3, 4, 5 are being given and a three digit code has to be made from it if the repetition of digits is allowed then how many such codes can be formed
We have five options for each digit of the code. Therefore the answer is 5•5•5= 125
100
In how many ways can a coach choose three swimmers from among five swimmers?
There are 5 swimmers to be taken 3 at a time.
Using the formula:
5•4•3/3•2•1= 10
100
what are outcomes?
possible results for an event
100
Mutually exclusive events DO NOT
happen at the same time
100
What is the conditional probability formula?
P(B/A)
200
If three alphabets are to be chosen from A, B, C, D and E such that repetition is not allowed then in how many ways it can be done?
5•4•3•2•1/2•1=60
200
Six friends want to play enough games of chess to be sure every one plays everyone else. How many games will they have to play?
There are 6 players to be taken 2 at a time.
Using the formula:
6•5/2•1= 15
200
Define theoretical probability
It is the probability of what should occur
200
True or False are turning left and turning right mutually exclusive
true
200
what is the definition for conditional probability?
the probability of an event occurring given that another event has occurred.
300
10 students have appeared in a test in which the top three will get a prize. How many possible ways are there to get the prize winners?
We need to choose and arrange 3 persons out of 10. Therefore, the number of possible ways will be
10!/(10-3)!= 10•9•8=720
300
Find the combination: 
126
300
what is experimental probability?
the probability of what actually occurs
300
Is tossing a coin mutually exclusive
yes
300
Out of 50 people surveyed in a study, 35 smoke in which there are 20 males. What is the probability the if the person surveyed is a smoker then he is a male?
Probability of the person being male and a smoker, 20/50
Probability of person being smoker, 35/50
P(B\A)= 20/35= 1/7
400
Ellie want to change her password which is ELLIE9 but with same letters and number. In how many ways she can do that?
Total number of letters = 6.
Repeated letters = 2 Ls and 2 Es.
Number of times ELLIE9 can be rearranged: 6!/2!2!= 6•5•3•2•1=180
But the password need to be changed. So, the number of ways new password can be made: 180-1=179
400
How many ways are there to choose 3 people to receive a $100 prize from a group of 9, assuming no one receives more than one prize?
9!/6!3!= 9•8•7/3•2•1=84
400
What is an independent event?
When one event occurs and the item is replaced before the second event occurs
400
True or false is drawing a red card and a king mutually exclusive?
false
400
The probability of rain on sunday is 0.07. If today is sunday, find the probability of rain today.
Probability that it is raining and the day is Sunday, 0.07
Probability that is is Sunday, 1/7
Probability it will rain if it is Sunday 1/7/.07= 0.49
500
How many ways can you choose a President, secretary and treasurer for a club from 12 candidates, if each candidate is eligible for each position, but no candidate can hold 2 positions?
12!/(12-3)= 12•11•10=1,320
500
In a lottery, each ticket has 5 one-digit numbers 0-9 on it.
You win if your ticket has the digits in any order. What are your changes of winning?
There are 10 digits to be taken 5 at a time.
Using the formula:
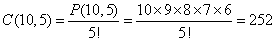
The chances of winning are 1 out of 252.
500
Define dependent event
When one event occurs and that item is not replaced before the second event occurs
500
Is Rolling a number divisible by 2 or rolling a number divisible by 3 mutually exclusive?
no
500
In a school the third language has to be chosen between Hindi and French. If a student has taken French then what is the probability that he will take Hindi, if the probability of taking Hindi is 0.34?
The probability of taking french and hindi is 0