Exponent Rules
Exponential Equations
Modeling
Growth vs. Decay
Vocabulary
100
EVALUATE the expression.
(2/3)^0
1
100
Identify the INITIAL VALUE.
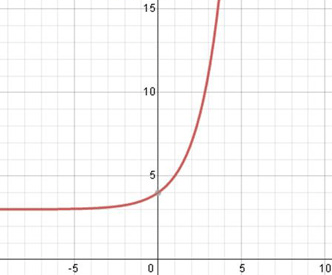
A=4
(0,4)
100
Write an EXPONENTIAL EQUATION for the situation.
"Mr. Becker invested $300 for his daughter Emma's college fund. The investment doubles every year."
C(t)=300*(2)^t
100
Does the graph show exponential GROWTH or DECAY?
Exponential Growth
Output goes to negative infinity.
100
What do we call the 4 in this exponential equation:
y=5*(4)^x
base or common ratio
200
EVALUATE the expression.
-3^4
-81
200
Identify the Y-INTERCEPT.
y=34*(3/2)^x
(0,34)
200
Write an EXPONENTIAL EQUATION for the situation.
"At the end of the year a students knows 80 vocabulary words. A student loses 5% of their memory of vocabulary words every month that they are not in school."
W(m)=80*(0.95)^m
200
Does the graph show exponential GROWTH or DECAY?
y=-32*(1.05)^x
Exponential Growth
(the common ratio is GREATER than 1)
200
The result of division.
Quotient
300
EVALUATE the expression.
(c^7)^8/(c^9)^6
c^4
300
Identify the COMMON RATIO.
r=2
300
Write an EXPONENTIAL EQUATION for the situation.
"In 2005, the population of the United States was about 296 million people. The annual rate of growth in the population is about 1%."
P(t)=296,000,000*(1.01)^t
300
What is the PERCENT of growth or decay?
y=100*3^x
200% growth
300
The INITIAL VALUE of an exponential functions is also this key feature on a graph.
y-intercept
400
SIMPLIFY the expression.
((3x)/(4x^2))^-2
(16x^2)/9
400
EVALUATE the exponential function.
f(x)=18*(3/2)^x
f(-2)=
f(-2)=8
400
You purchased a new computer for $1500. It decreases in value by about –18% each year. How much will your computer be worth in 6 years?
About $456
400
What is the PERCENT of growth or decay?
y=20*(5/4)^x
25% growth
400
What do we call two numbers whose product is 1?
This is what negative exponents create.
Reciprocals
500
SIMPLIFY the expression.
(24x^6)/((2x)^3(6x^-5))
x^8/2
500
Solve for x.
2^(3x+7)=2^(4x-1)
x=8
500
E.Coli. bacteria reproduce at a growth rate of 125% per hour. If after 4 hours there are 150,000 bacteria infecting a person, approximately how many bacteria were there initially?
Initially there were approximately 5853 bacteria.
500
What is the PERCENT of growth or decay?
75% decay
500
What rule is shown?
(a^3/b^2)^4=a^12/b^8
Power of a Quotient Rule