Is this graph represent exponential GROWTH or DECAY?

EXPONENTIAL GROWTH
The outputs (y-values) are "growing" or getting larger in the negative direction. The outputs will approach negative infinity.
Does this exponential function model GROWTH or DECAY?
y=0.75(5/6)^x+3
DECAY
The common ratio (r) in this equation is less than 1 which indicated decay (the outputs are getting smaller by a factor of 5/6 for every increase of 1 in the input.
What is the OUTPUT of a LOGARITHMIC function?
an EXPONENT
Logarithms are the inverse of exponential functions and used when solving exponential equations where the exponent is unknown. The output of a logarithm is an exponent.
Write the END BEHAVIOR of this graph.
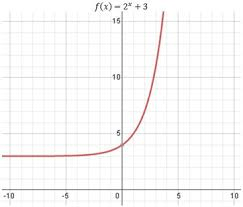
x->oo f(x)->oo
x->-oo f(x)->3
Write the exponential equation for the table below.
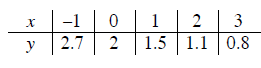
Estimate the value of log3 (90) WITHOUT a calculator.
xapprox4.1
Since 34=81 and 35=243, we can see x must be between 4 and 5. Since 90 is much closer to 81 than 243, we can estimate the value to be slightly over 4.
What are the restrictions on the BASE of an EXPONENTIAL function?
The base can be any positive number except 1.
0<base, base ne1
Write the equation of the exponential graph.
y=4/9(3/2)^x
Solve for the exponential equation WITHOUT using logarithms or a calculator.
2^(3x)=64
x=2
Since 26=64 we can rewrite the equation as 23x=26. That means 3x=6, so x=2.
Write the logarithm in EXPONENTIAL form.
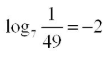
7^-2=1/49
Solve the exponential equation WITHOUT using logarithms or your calculator.
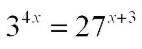
x=9
Since 27x+3=(33)(x+3) we can rewrite the equation as 34x=33x+9. That means 4x=3x+9, so x=9.
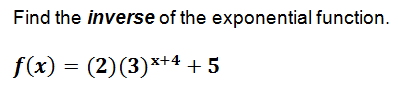
y=log_3((x-5)/2)-4
The inverse of an exponential function is a logarithm. So rewrite the original function in logarithmic form by switching x and y and then isolating y.
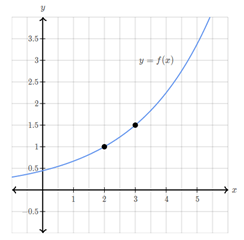
f(-1)=27 and f(2)=1 are coordinates that can be found using an exponential equation. Find the equation that created these points.
f(x)=9(1/3)^x
Set up a system of equations. Isolate r or A and then use substitution to solve.
Solve for x WITHOUT a calculator.
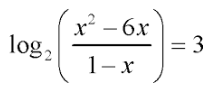
x=-2 and 4
First write the equation in exponential form. Then use Algebra to isolate x.
2^3=(x^2-6x)/(1-x)