End Behavior
Identifying Zeros and Multiplicities
Determining a Function Type
100
Determine the end behavior of the graph (MUST WRITE IN CORRECT NOTATION)
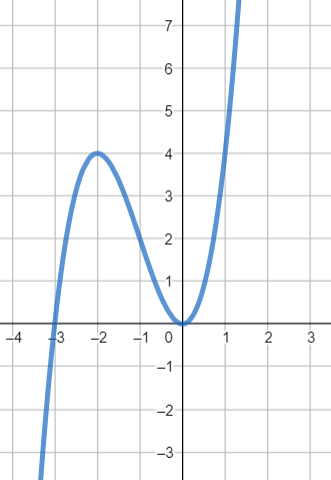
Down/up
100
What are the zeros and their multiplicities of the graph?
0 multi 1
-6 multi 1
100
What is the smallest possible degree of the function this graph represents? 
5th
200
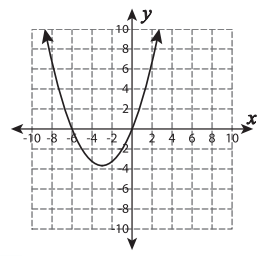
Determine the end behavior of the function (Use correct notation)
g(x)=2x^4+7
up/up
200
Identify the zeros and their multiplicities of the graph
-3 multi 1
-0.5 multi 1
-4 multi 1
200
What is the smallest possible degree of the function this graph represents?
6th degree
300
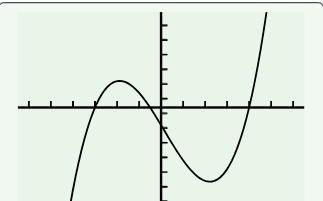
Determine the end behavior of the function (Use correct notation)
f(x)=x^5+5
Down/Up
300
Identify the zeros and their multiplicities of the function
f(x)=x^2(x-1)^2(x+3)
0 multi of 2
1 multi 2
-3 multi 1
300
What are the zeros and the multiplies of the function on the graph?
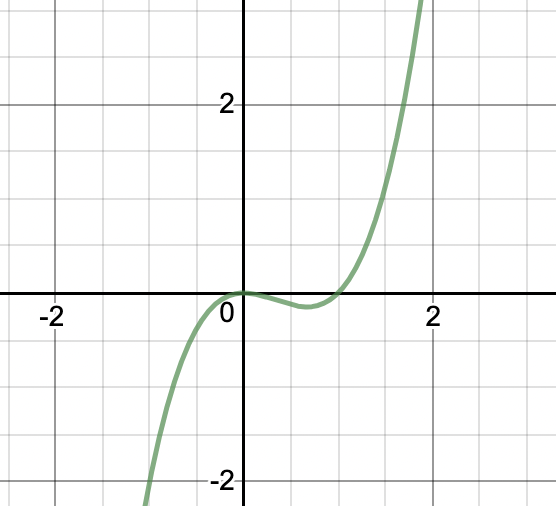
0 multi of 2
1 multi of 1
400
Determine the end behavior of the function (Use correct notation)
g(x)=-9x^4+2x^2-x
down/down
400
Identify the zeros and their multiplicities. Then determine the degree of the function.
f(x)=-x(x+7)^3(x+2)^2
o multi 1
-7 multi 3
-2 multi 2
6th degree
400
If a function has the following characteristics
-3 real zeros each with a multiplicity of 2
-a negative leading coefficient
What is the end behavior?
down/down
500
Determine the end behavior of the function (Use correct notation)
f(x)=-x^7+x^4+3
up/down
500
Identify the zeros and their multiplicities. Then determine the degree of the function.
f(x)=x^2(x-5)^5(x+1)^2(x+4)
0 multi 2
5 multi 5
-1 multi 2
-4 multi 1
10th degree
500
If a function has the following characteristics
-3 real zeros each with a multiplicity of 1
-a real zero with a multiplicity of 3
What is the degree of the function?
6th