Quelle est la formule pour calculer le volume d'un prisme rectangulaire?
Volume = longueur ⋅ épaisseur ⋅ hauteur
ou
Volume = aire de la base ⋅ hauteur
Quelle est la formule pour calculer le volume d'un prisme triangulaire?
Volume = (longueur ⋅ épaisseur ÷ 2) ⋅ hauteur
ou
Volume = aire de la base ⋅ hauteur
Quelle est la formule pour calculer le volume d'un prisme trapézoïdal?
Volume = (base1 + base2) ⋅ longueur ÷ 2 ⋅ hauteur
ou
Volume = aire de la base ⋅ hauteur
Quelle est la formule pour calculer le volume d'un cylindre?
Volume = π ⋅ r2 ⋅ hauteur
ou
Volume = aire de la base ⋅ hauteur
Vrai ou Faux: Le volume est mesuré en unités carrés parce que c'est un mesurement à deux dimensions.
Faux. Le volume est mesuré en unités cubes parce que c'est un mesurement à trois dimensions.
Une longueur de 15 m
Une épaisseur (width) de 6 m
Une hauteur de 9 m
Volume = longueur ⋅ épaisseur ⋅ hauteur
V = 15 ⋅ 6 ⋅ 9
V = 90 ⋅ 9
V = 810 m3
Une longueur de 15 m
Une épaisseur (width) de 6 m
Une hauteur de 9 m
Volume = (longueur ⋅ épaisseur ÷ 2) ⋅ hauteur
V = (15 ⋅ 6 ÷ 2) ⋅ 9
V = (90 ÷ 2) ⋅ 9
V = 45 ⋅ 9
V = 405 m3
Une base1 de 9 m
Une base2 de 27 m
Une longueur de 10 m
Une hauteur de 4 m
Volume = (base1 + base2) ⋅ longueur ÷ 2 ⋅ hauteur
V = (9 + 27) ⋅ 10 ÷ 2 ⋅ 4
V = 36 ⋅ 10 ÷ 2 ⋅ 4
V = 360 ÷ 2 ⋅ 4
V = 180 ⋅ 4
V = 720 m3
Un rayon de 4 m
Une hauteur de 10 m
Volume = π ⋅ r2 ⋅ hauteur
V = π ⋅ (4)2 ⋅ 10
V = π ⋅ (16) ⋅ 10
V = π ⋅ (160)
V = 502,6 m3
Un carton de jus d’orange a une longueur de 10 cm, une épaisseur (width) de 4 cm, et une hauteur de 18 cm.
Qu’est-ce que c’est le volume du carton de jus?
Volume = longueur ⋅ épaisseur ⋅ hauteur
V = 10 ⋅ 4 ⋅ 18
V = 40 ⋅ 18
V = 720 cm3
Une longueur de 90 mm
Une épaisseur (width) de 42 mm
Une hauteur de 17 mm
Volume = longueur ⋅ épaisseur ⋅ hauteur
V = 90 ⋅ 42 ⋅ 17
V = 3780 ⋅ 17
V = 64 260 mm3
Une longueur de 90 mm
Une épaisseur (width) de 42 mm
Une hauteur de 17 mm
Volume = (longueur ⋅ épaisseur ÷ 2) ⋅ hauteur
V = (90 ⋅ 42 ÷ 2) ⋅ 17
V = (3780 ÷ 2) ⋅ 17
V = 1890 ⋅ 17
V = 32 130 mm3
Une base1 de 6 mm
Une base2 de 13 mm
Une longueur de 15 mm
Une hauteur de 9 mm
Volume = (base1 + base2) ⋅ longueur ÷ 2 ⋅ hauteur
V = (6 + 13) ⋅ 15 ÷ 2 ⋅ 9
V = 19 ⋅ 15 ÷ 2 ⋅ 9
V = 285 ÷ 2 ⋅ 9
V = 142,5 ⋅ 9
V = 1282,5 mm3
Un diamètre de 12 mm
Une hauteur de 9 mm
Volume = π ⋅ r2 ⋅ hauteur
V = π ⋅ (6)2 ⋅ 9
V = π ⋅ (36) ⋅ 9
V = π ⋅ (324)
V = 1017,8 mm3
Un grand casier (locker) est au-dessous (under) d'un petit casier. Chaque casier a une longueur de 0,6 m et une épaisseur (width) de 0,8 m. Le grand casier a une hauteur de 1,4 m et le petit casier a la moitié (half) de cette hauteur.
Qu’est-ce que c’est le volume du petit casier?
Les dimensions du grand casier:
0,6m par 0,8m par 1,4m
Les dimensions du petit casier:
0,6m par 0,8m par 0,7m
Volume = longueur ⋅ épaisseur ⋅ hauteur
V = 0,6 ⋅ 0,8 ⋅ 0,7
V = 0,336 m3
Quel est le volume de ce prisme rectangulaire?
Volume = longueur ⋅ épaisseur ⋅ hauteur
V = 4 ⋅ 5 ⋅ 2
V = 20 ⋅ 2
V = 40 unités3
Quel est le volume de ce prisme triangulaire?

Volume = (longueur ⋅ épaisseur ÷ 2) ⋅ hauteur
V = (5 ⋅ 4,5 ÷ 2) ⋅ 8
V = (22,5 ÷ 2) ⋅ 8
V = 11,25 ⋅ 8
V = 90 cm3
Quel est le volume de ce prisme trapézoïdal?

Volume = (base1 + base2) ⋅ longueur ÷ 2 ⋅ hauteur
V = (8 + 14) ⋅ 4 ÷ 2 ⋅ 10
V = 22 ⋅ 4 ÷ 2 ⋅ 10
V = 88 ÷ 2 ⋅ 10
V = 44 ⋅ 10
V = 440 cm3
Quel est le volume de ce cylindre?

Volume = π ⋅ r2 ⋅ hauteur
V = π ⋅ (8)2 ⋅ 15
V = π ⋅ (64) ⋅ 15
V = π ⋅ (960)
V = 3015,8 cm3
La pyramide de Gizeh en Egypte a une base carrée (square). Chaque côté de la base mesure 345 m et la hauteur de la pyramide est 225 m.
Qu’est-ce que c’est le volume de la pyramide?
V = (b2) ⋅ h ÷ 3
ou
V = (b ⋅ b) ⋅ h ÷ 3
V = (345 ⋅ 345) ⋅ 225 ÷ 3
V= 119025 ⋅ 225 ÷ 3
V = 26 780 625 ÷ 3
V = 8 926 875 m3
Quel est le volume de ce prisme rectangulaire?
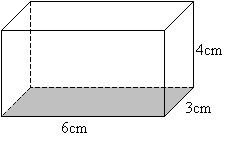
Volume = longueur ⋅ épaisseur ⋅ hauteur
V = 6 ⋅ 3 ⋅ 4
V = 18 ⋅ 4
V = 72 cm3
Quel est le volume de ce prisme triangulaire?

Volume = (longueur ⋅ épaisseur ÷ 2) ⋅ hauteur
V = (6 ⋅ 4 ÷ 2) ⋅ 12
V = (24 ÷ 2) ⋅ 12
V = 12 ⋅ 12
V = 144 cm3
Quel est le volume de ce prisme trapézoïdal?

Volume = (base1 + base2) ⋅ longueur ÷ 2 ⋅ hauteur
V = (6 + 12) ⋅ 4 ÷ 2 ⋅ 10
V = 18 ⋅ 4 ÷ 2 ⋅ 10
V = 72 ÷ 2 ⋅ 10
V = 36 ⋅ 10
V = 360 cm3
Quel est le volume de ce cylindre?
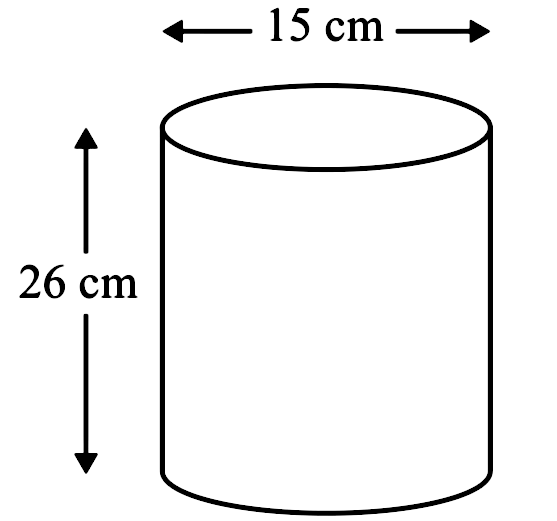
Volume = π ⋅ r2 ⋅ hauteur
V = π ⋅ (7,5)2 ⋅ 26
V = π ⋅ (56,25) ⋅ 26
V = π ⋅ (1462,5)
V = 4594,4 cm3
Un sac en papier a une longueur de 15 cm, une épaisseur (width) de 7 cm, et une hauteur de 24 cm.
À l'intérieur du sac se trouve une boîte (box) qui a une longueur de 7 cm, une épaisseur (width) de 4 cm, et une hauteur de 13 cm.
Combien d'espace (space) reste-t-il dans le sac?
Volume du sac en papier:
Volume = longueur ⋅ épaisseur ⋅ hauteur
V = 15 ⋅ 7 ⋅ 24
V = 2520 cm3
Volume de la boîte:
Volume = longueur ⋅ épaisseur ⋅ hauteur
V = 7 ⋅ 4 ⋅13
V = 364 cm3
Volume de l'espace qui reste:
V = 2520 - 364
V = 2156 cm3