Divide & Conquer?
Picture This!
Get it RIGHT
There's PROBABLY a Trick to This
Terminally Based
300
How many positive divisors does 7380 have?
7380 = 2^2*3^2*5*41
3*3*2*2=36 .
300
It is known that if you want to color a map so that adjacent regions always have different colors, only 4 colors are required.
How many ways are there to color the map below in red, blue, green, and yellow, so that no two adjacent regions have the same color?
If we choose a color arrangement for A, B, C, D, the rest of the map is determined.
4! = 24.
300
In triangle ABC, angle A = 90 degrees, AB = 6, and BC = 10. Compute the length of altitude AH.
Triangles HBA, HAC, and ABC are all similar: their sides are 3k, 4k, 5k.
AH = 4.8
300
Four pennies and four dimes are placed in a row. What is the probability that the row begins and ends with a dime?
1/2 *3/7 = 3/14
300
Suppose 100! is computed, and the result written in base 7. How many terminal zeros will appear? (Terminal zeros are the ones at the right end of a number.)
Answer: 16
There are 16 powers of 7 in 100! Here's how to count the powers quickly:
100/7 = 14 (R 2).
14/7 = 2 (R 0).
2/7 = 0 (R 2).
14 + 2 = 16.
400
How many positive divisors of 10,000,000,000 are perfect cubes?
10^10=2^10*5^10.
Powers of prime factors of perfect cubes are divisible by 3.
4*4=16.
400
A chess knight usually moves as shown below. But suppose a certain knight is allowed to move only up and to the right. In how many ways can this knight move from the lower left corner of the board to the upper right corner?
The answer is zero.
The two squares are on the same diagonal, so the knight has to move as far up as it moves right. It can only do this in multiples of 3 squares.
400
In triangle ABC, angle A = 90 degrees, AB = 5, and BC = 13. AH is the altitude from A to side BC. Compute the area of triangle ABH. Write your answer as a common (improper) fraction.
Triangles ABH, CAH, and CBA are all similar: their sides are 5k, 12k, 13k.
1/2*25/13*60/13=750/169
400
Three 8-sided dice are rolled. The faces of each die show the numbers 1 through 8. What is the probability that the sum of the values of the dice will be exactly 10?
83=512 results are possible. By stars and bars, a sum of 10 can be obtained in (9 choose 2) = 36 ways.
36/512 = 9/128
400
Suppose 100! is computed, and the result written in base 12. How many terminal zeros will appear?
Answer: 48
12 = 22*3.
There are 97 powers of 2 in 100!. 97 has 48 pairs of 2's, with one 2 left over that we can't use.
There are 48 powers of 3 in 100!.
We would take the lesser of the two results, but it happens that they are equal.
500
What is the 10th largest divisor of 12,000?
We can find it by dividing by the 10th smallest divisor, which is 15.
12,000 div15=800 .
500
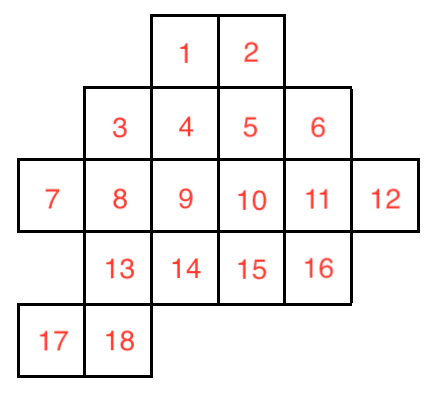
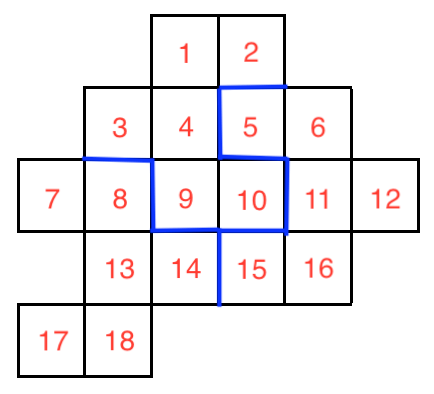
Cutting only along grid lines, split the shape into 3 parts which are equal in shape and size. (You may answer by splitting the numbers into three sets that compose the three parts.)
500
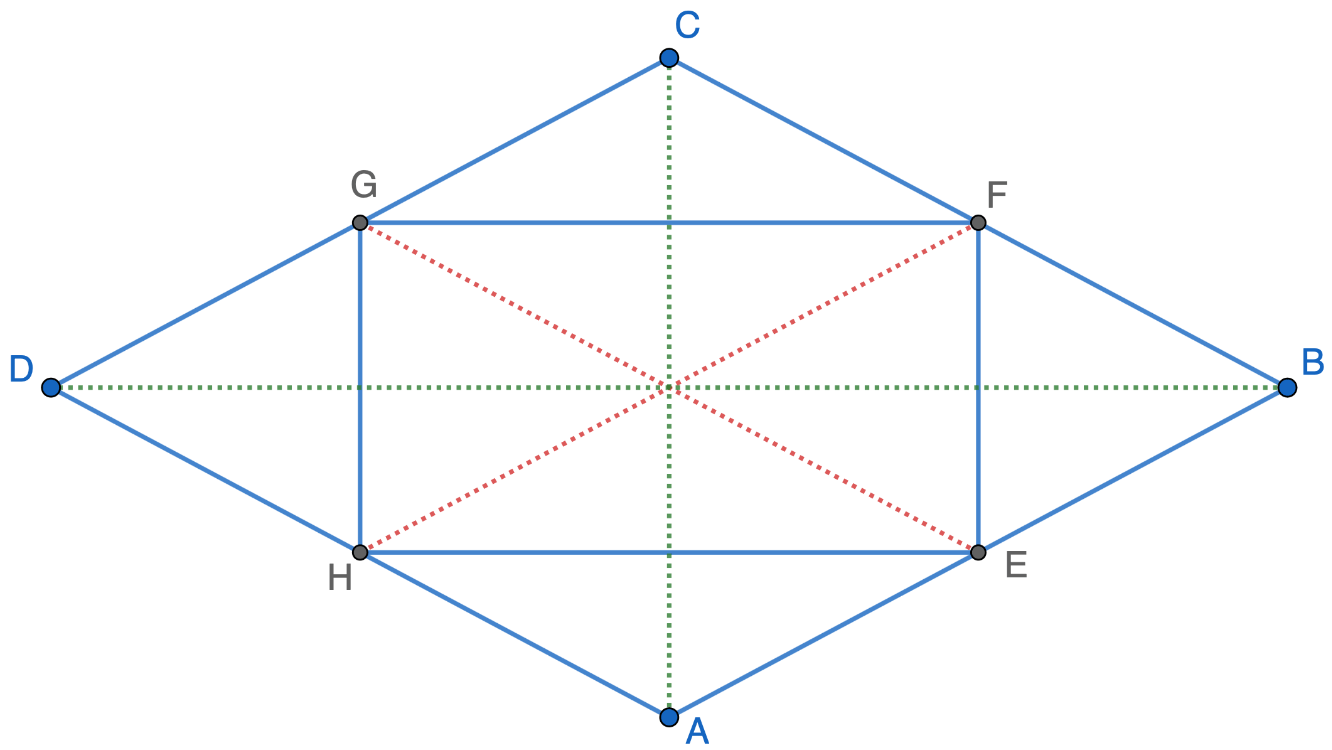
Rectangle EFGH is constructed by connecting the midpoints of rhombus ABCD, as shown below. If the rhombus has perimeter 68, and EF = 8, what is the area of the rhombus?
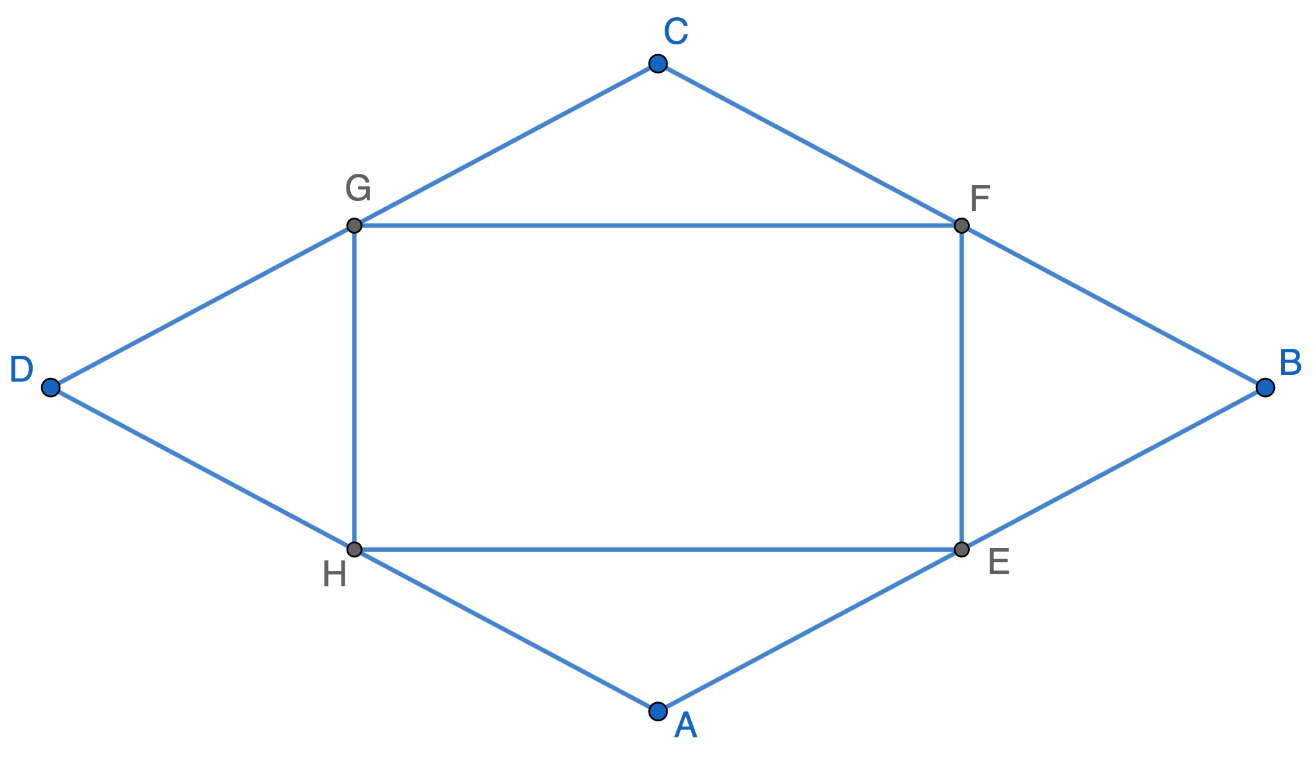
As illustrated below, the rhombus comprises 4 congruent right triangles, each congruent to right triangle HEF, which has sides of 8, 15, and 17. Its area is 4*1/2*8*15 = 240.
500
Players 1 through 5 play a dice game, using a six-sided die. In a given turn, if a player rolls a 6, that player wins the game. If any other number is rolled, the next turn goes to the player with that number—even if it is the number of the player who is rolling the die. Player 1 goes first.
What is the probability that Player 1 will win the game?
There's a 1/6 chance that Player 1 will roll a 6 and win immediately.
There's a 5/6 chance that Player 1 will roll something else. In that case, all 5 players have an equal chance of winning.
1/6 + 5/6 *1/5 =1/3 .
500
Suppose that
499times497times495times...times3times1
is computed, and the result written in base 7. How many terminal zeros will appear?
Answer: 42
There are 71 multiples of 7 less than 499, 36 of them odd.
Among those are 10 multiples of 72, 5 of them odd.
Among those is 1 multiple of 73, and it is odd.
We want the odd multiples: 36+6+1=42.