BLITZ:
"Minds that Count"
"Minds that Count"
You'll Probably Be Fine.
Mods & Bases
Hazardous Area!
Surprise Me!
300
Angie is purchasing stickers to make house numbers for the houses in her neighborhood. If the houses are numbered consecutively from 101 to 250 and each sticker contains a single digit, how many stickers containing the digit 3 does Angie need to purchase?
3 appears 150/10 = 15 times as a units digit, and 20 times as a tens digit.
35 is the answer.
300
What is the probability of rolling six standard, six-sided dice and obtaining six different values?
{6!}/{6^6}=5/324
300
The number of students in Teresa’s graduating class is more than 50 and fewer than 100 and is 1 less than a multiple of 3, 2 less than a multiple of 4, and 3 less than a multiple of 5. How many students are in Teresa’s graduating class?
The number is equivalent 2 (mod 3), 2 (mod 4), 2 (mod 5), i.e. it is 2 (mod 60).
Answer: 62
300
In the figure shown, arc ADB and arc BEC are semicircles, each with a radius of one unit. Point D, point E and point F are the midpoints of arc ADB, arc BEC and arc DFE, respectively. If arc DFE is also a semicircle, what is the area of the shaded region?
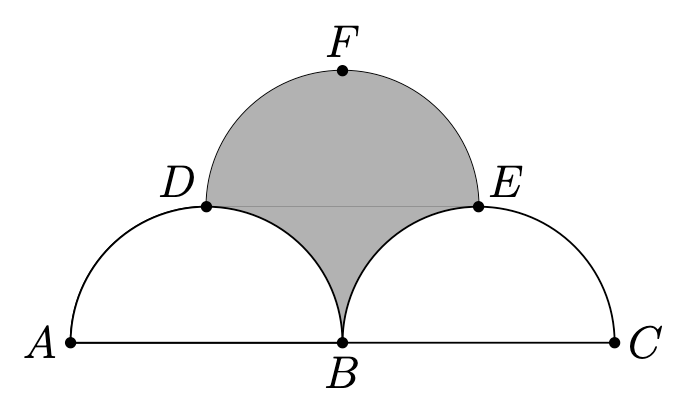
The area is the same as the area of a rectangle with base DE = 2 and height DE/2 = 1.
Answer: 2
300
The pages of a book are numbered consecutively beginning with page 1. Given that 768 digits are used to number the pages of the book, how many pages does the book contain?
9 + 180 = 189 digits are used for pages 1-99.
The other 579 digits are used for pages 100 and up.
Answer: 292.
400
The 5-digit integer
bar{RS,TUV}
is divisible by 5. If
S=R^2,
and
10T+U=5,
how many different values can the number have?
T and U are determined. V is 0 or 5. R is 1, 2, or 3.
Answer: 6.
400
A committee of six students will be chosen randomly from a group consisting of six boys and four girls. What is the probability that the committee will contain the same number of boys as girls?
{([6],[3])([4],[3])}/{([10],[6])} =80/210=8/21
400
What is the sum of the last two digits of the following portion of the Fibonacci Factorial Series?
1!+1!+2!+3!+5!+8!+13!+21!+34!+55!+89!
Starting with 13!, all the terms are 0 (mod 100). The sum of the first 6 terms is 50 (mod 100).
Answer: 5
400
In triangle ABC shown below, AE = 6, AC = 10, and segment DE is parallel to segment BC. If triangle ABC has an area of 250, what is the area of trapezoid DBCE?
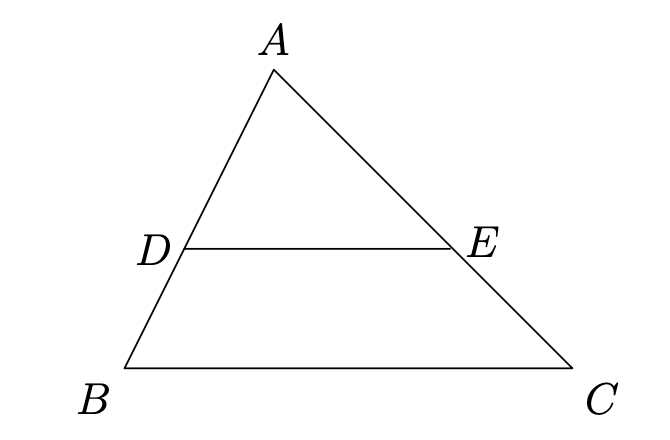
triangleABC ~ triangleADE.
[ABC]:[ADE]=10^2:6^2=100:36=25:9.
[ADE]=90\Rightarrow [DBCE]=160.
400
Pipe A will fill a tank in 6 hours. Pipe B will fill the same tank in 4 hours. Pipe C will fill the tank in the same number of hours that it will take Pipes A and B working together to fill the tank. What fraction of the tank will be filled if all three of the pipes work together for one hour? Express your answer as a common fraction.
In 1 hour, A fills 1/4 of the tank, and B fills 1/6. Working together, they fill 5/12 of the tank. C does the same by itself.
Answer: 5/6.
500
What fraction of the first 100 triangular numbers are divisible by 7?
A triangular number {n(n+1)}/2 is divisible by 7 iff n or n + 1 is a multiple of 7. There are 28 such numbers from 1 through 100.
Answer: 7/25.
500
Bag A contains 3 white and 2 red balls. Bag B contains 6 white and 3 red balls. One of the two bags will be chosen at random, and then two balls will be drawn from that bag at random without replacement. What is the probability that the two balls drawn will be the same color? Express your answer as a common fraction.
1/2*2/5 +1/2*1/2 =9/20
500
The base 9 representation of a positive integer is bar{AB} and its base 7 representation is bar{BA} . What is the integer expressed in base 10?
9A+B=7B+A Rightarrow 4A=3B.
Then 4 | B. B can't be 0 or 8, so B = 4, A = 3, and
7B+A=31.
500
Given that BDEF is a square and AB = BC = 1, find the area of the regular octagon. (In a regular polygon, all sides are equal.)
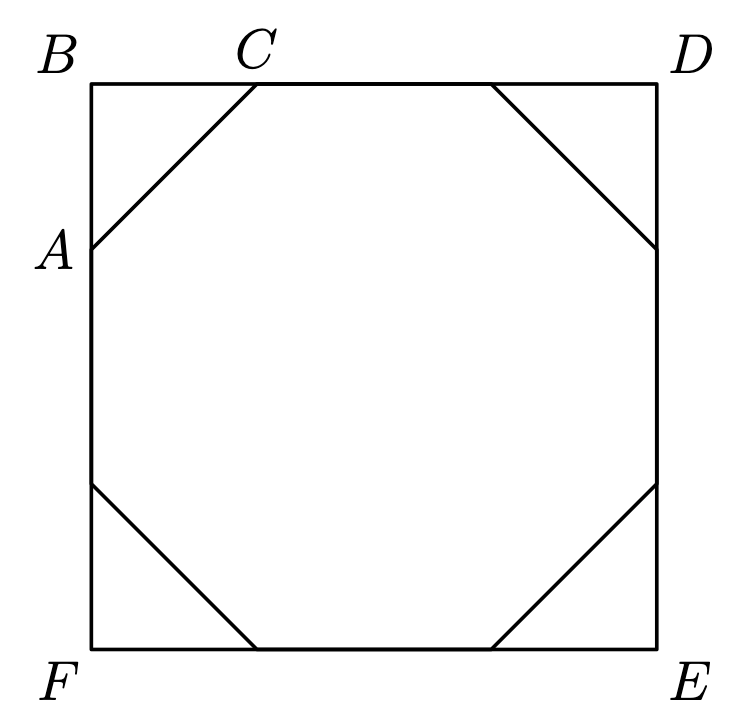
The square has sides of length 2+sqrt2 , so its area is 6+2sqrt2 We subtract the areas of the four 45-45-90 triangles to find
4 + 4sqrt2
500
The first three terms of a geometric sequence are
3,6+p,text{and }30-p,
and each term is a positive number. What is the fifth term of this sequence?
Consecutive terms have a common ratio, so
3/{6+p} = {6+p}/{30-p}
We find p by solving a quadratic. Only p = 3 produces all positive terms. Subbing this in, we get
3, 9, 27, 81, 243.