Tables
Graphs
Rate of Change and
Exponent Properties
Exponent Properties
Applications #1
Applications #2
100
Create the equation that is modeled in the table below.
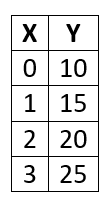
y=5x+10
100
Create an equation for the function graphed below.
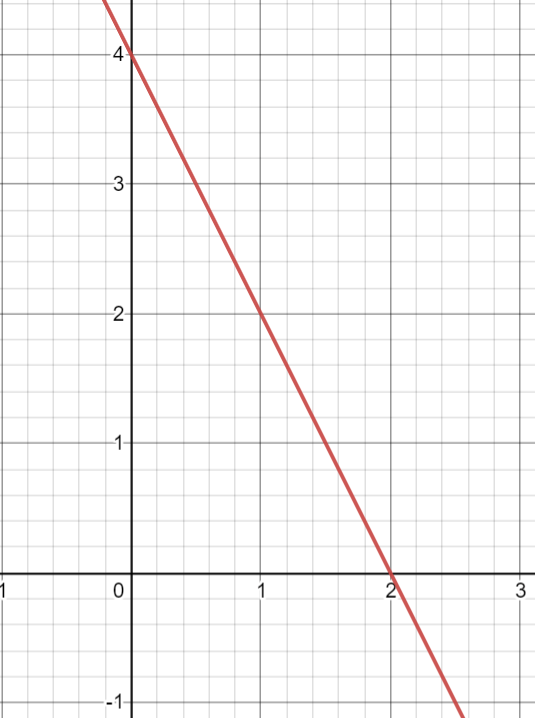
y=-2x+4
100
Find the rate of change between the two points below.
(1, 4) and (5, 20)
2
100
Josie started a savings account. She deposited $500 when she opened the account. She is going to add $50 each month into the account. Create an equation to model the amount of money Josie has in her account after each month.
A=50m+500
100
A single bacteria is placed in a petri dish and is observed every day. Each day the bacteria doubles. Create an equation to model the number of bacteria in the petri dish each day.
B=1(2)^x
200
Create the equation that is modeled in the table below.
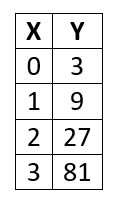
y=3(3)^x
200
Create an equation for the function graphed below.
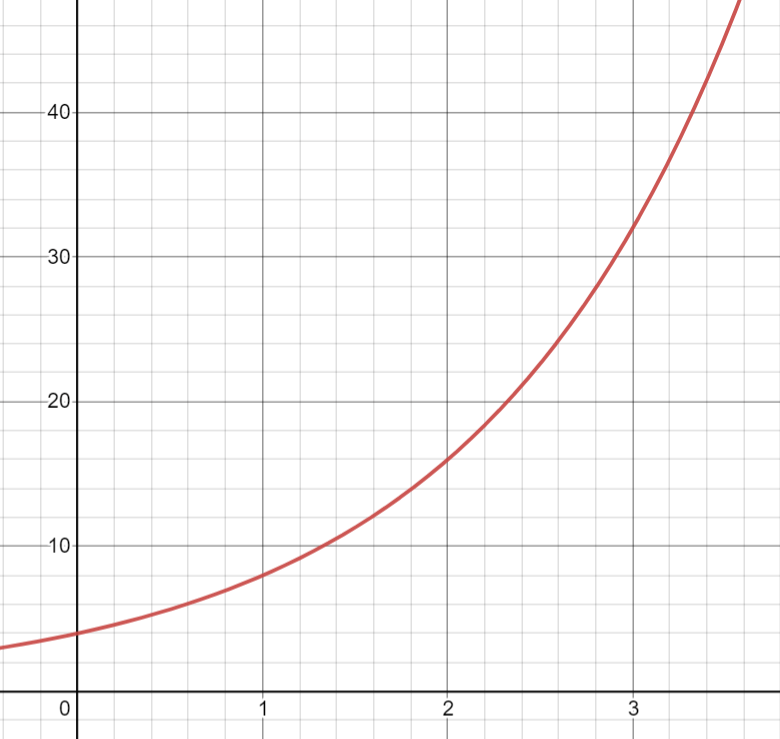
y=4(2)^x
200
The table below shows the population of a City from the year 2000 to 2020. What is the average rate of change from the year 2000 to 2020?
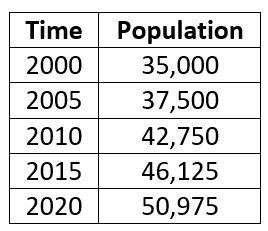
15975/20 people per year
798.75 people per year
200
Jiminy Cricket is 3 feet from his house when it starts to rain. As more rain falls, Jiminy can not jump as far. On his first jump, he makes it 1.5 feet or half the distance to his house. Each jump after that, Jiminy can only jump half of the distance of his previous jump.
a) Create a function to model this situation.
b) How far will Jiminy be after 8 jumps?
a) D=3(1/2)^x
b) 0.0117 feet
200
A new cell phone company is releasing a new plan. The plan consists of paying a base fee of $60 per month and $8 per gigabyte of data used.
a) Create a function that models this situation.
b) How much will a monthly bill be if 4 gigabytes are used?
c) If the total bill is $132, how many gigabytes were used that month?
a) C=8g+60
b) $92
c) 9 gigabytes
300
Create the equation that is modeled in the table below.
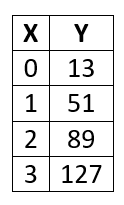
y=38x+13
300
Create an equation for the function graphed below.
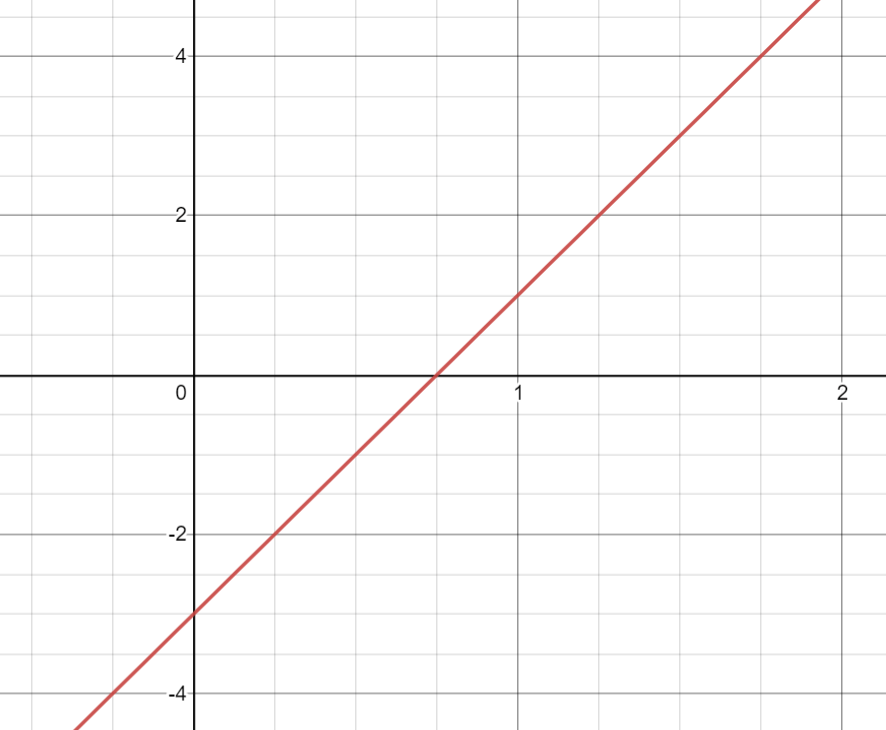
y=4x-3
300
Simplify the expression below. No negative exponents are allowed in the final answer.
(x^3y^8z^5)^4
x^12y^32z^20
300
A brand new Tesla Model S, costs $95,000. The car depreciates 18% per year.
a) Create a function that models the price of the Tesla after each year.
b) What is the price of the Tesla 5 years later?
a) V=95,000(0.82)^t
b) $35,220.29
300
Landon ate half a banana in his room and forgot to throw the rest away. That night, two gnats came to visit the banana. Each night after, there were four times as many gnats hanging around the banana.
a) Write a function that models the gnats' growth over time.
b) How many gnats are there are on night 6 if Landon does not throw away the banana?
a) G=2(4)^x
b) 8,192 gnats
400
Create the equation that is modeled in the table below. What is the value of x = 100?
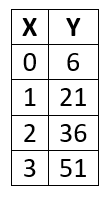
y=15x+6
y=1506
400
Create an equation for the function graphed below.
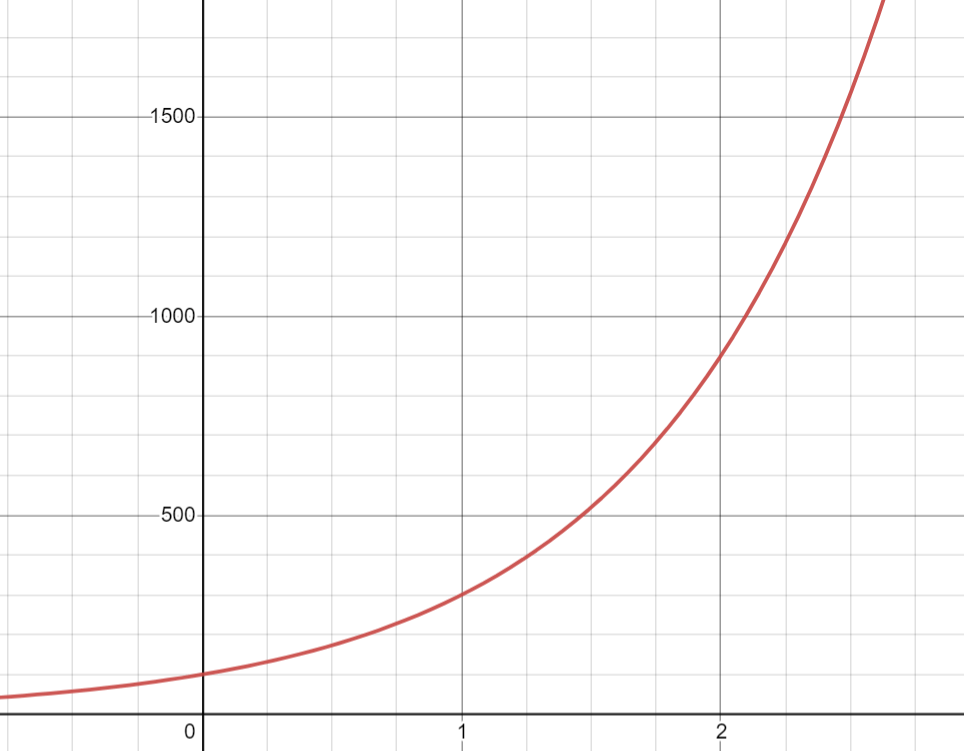
y=100(3)^x
400
Simplify the expression below. No negative exponents are allowed in the final answer.
(a^10b^14c^2)/(a^15b^8c^10)
(b^6)/(a^5c^8)
400
Every time Pinocchio lies, his nose grows 20% of its size. His original nose was 2 inches long.
a) Write an equation to model the length of Pinocchio's nose as a function of the number of lies he tells.
b) How long is his nose after 10 lies?
c) How many lies does he have to tell for his nose to first be over 3 feet long?
a) L=2(1.2)^x
b) 12.383 inches
c) 16 lies
400
Molly's parents invest $500 into an account the day she was born. The account is predicted to earn (grow) 9% interest each year.
a) Create a function to model the amount of money in the account each year.
b) How much money will be in the account when Molly turns 18? (There were no additional deposits made)
a) A=500(1.09)^x
b) $2358.56
500
Create the equation that is modeled in the table below. What is the value of x = 10?
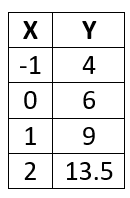
y=6(1.5)^x
345.99
500
Create an equation for the function graphed below. Then find the value of the function when x = 8.
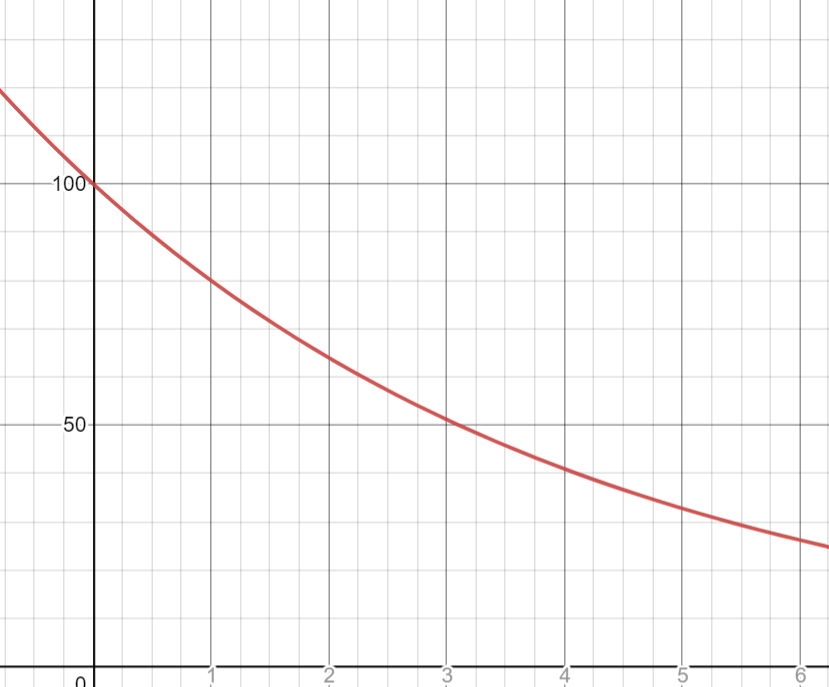
a) y=100(0.8)^x
b) 16.777
500
Simplify the expression below. No negative exponents are allowed in the final answer.
(3x^2y^4)(x^-3y^6)^3
(3y^22)/(x^7)
500
Due to a severe drought, a population of lions is decreasing at a rate of 3.5% per year. Scientists have noticed 80 lions in the area. a) Write a function to model the lion population each year.
b) What is the lion population after 3 years?
c) When will the lion population first be under 25 lions?
a) P=80(0.965)^x
b) About 71-72 Lions
c) 33 years later
500
Olaf drinks a soda that contains 120 mg of caffeine. Each hour, the caffeine in his system decreases by about 12%.
a) Create a function to model the amount of caffeine in Olaf's system after each hour.
b) How many mg of caffeine are in Olaf's system after 4 hours?
c) When is the first time there will be less than 50 mg of caffeine in Olaf's system?
a) C=120(0.88)^h
b) 71.963 mg
b) 7 hours later