Slope
Slope-Intercept
Point-Slope
Standard Form
Proportional Relationships
100
Identify what "m" and "b" represent in the following equation. y = mx + b
m is the slope
b is the y-intercept
100
What is slope-intercept formula?
y = mx + b
100
What is the point-slope formula?
y - y1 = m(x - x1)
100
What is the formula for Standard Form?
Ax + By = C
100
What is the formula for a proportional relationship/direct variation equation?
y = mx
200
Describe how you use a slope of -4/3 on a graph.
Ex. Up, down, left, right and how many places
Down 4, Right 3
200
Identify the slope and the y-intercept of the following equation:
y = -9x + 12
Slope = -9
y-intercept = (0, 12)
200
Write an equation in point-slope form that has a slope of -1/2 and passes through the point (5 , 7)
y - 7 = -1/2(x - 5)
200
What is the x and y intercepts of the following equation?
6x + 15y = 30
(5 , 0) and (0 , 2)
200
What two things need to be true for a relationship to be proportional?
Must reach (0,0) and slope must be consistent/the same
300
Identify the type of slope shown in the graph.
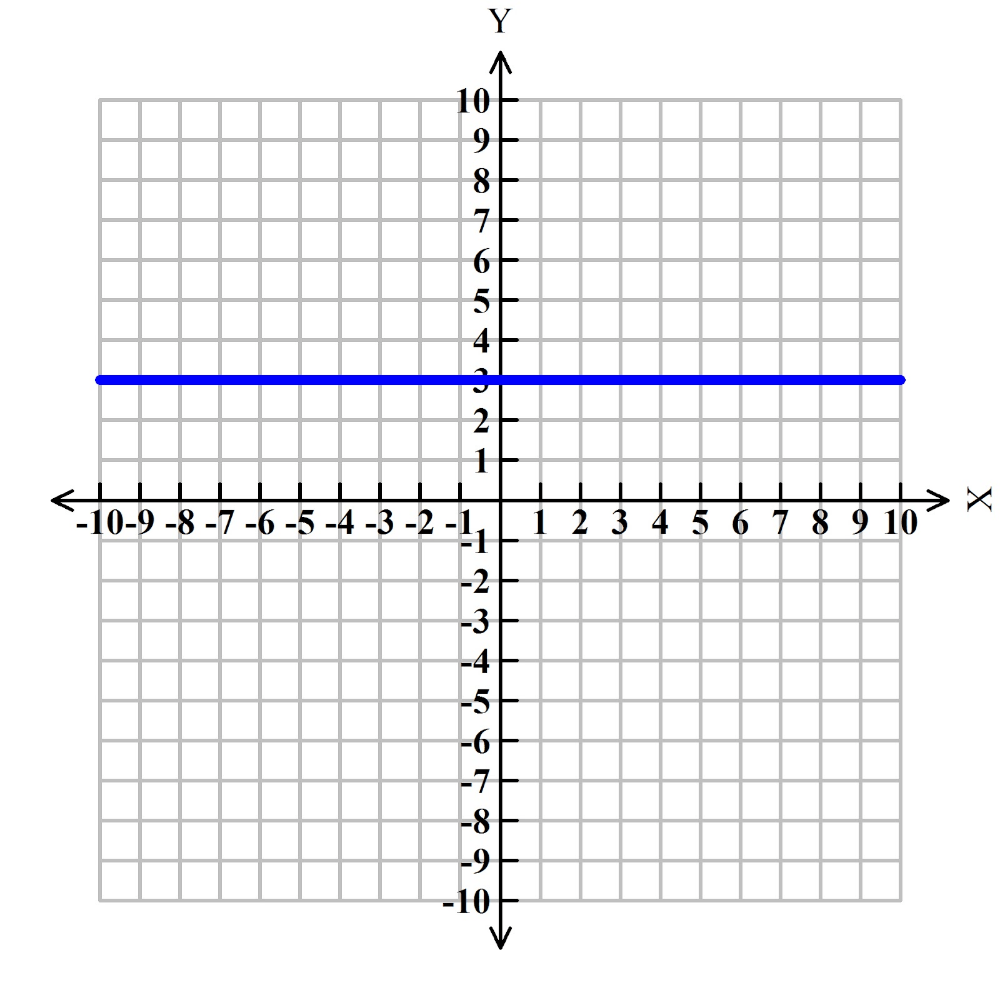
Zero Slope
300
Write an equation in Slope Intercept form for the line.
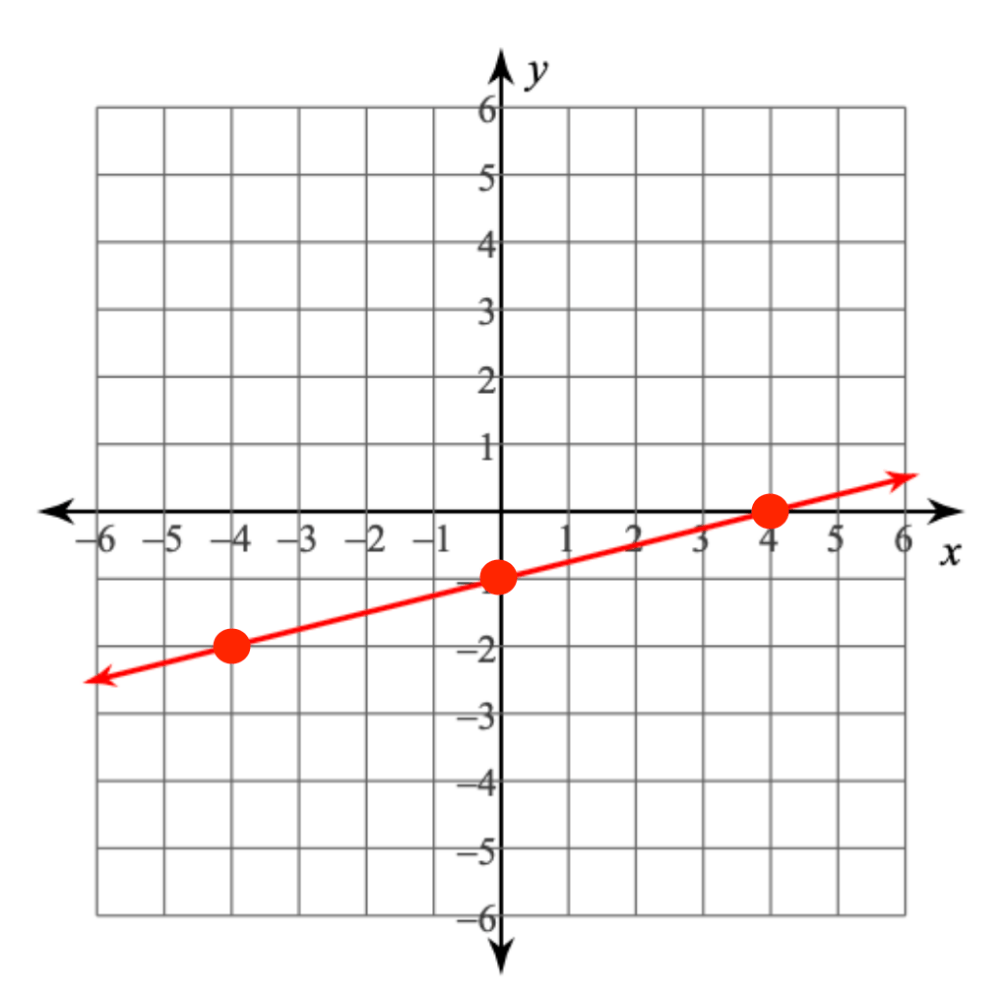
y=1/4x-1
300
Write an equation in Point-Slope form that passes through the point (-6, -2) and have a slope of m = 3.
y + 2 = 3(x + 6)
300
What is the x and y intercepts of the following equation?
4x - y = 12
(0, -12) and (3, 0)
300
Does the table represent a proportional relationship? Explain your reasoning.
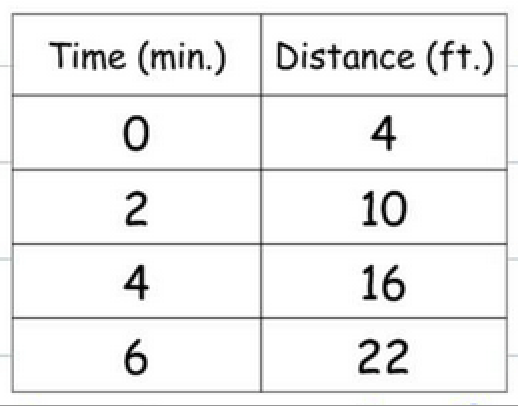
No - does not reach (0,0).
400
Find the slope of the line that includes the following points. (5, 4) (5, 8).
Identify the type of slope (positive, negative, zero, undefined).
4/0 which is Undefined
400
Write an equation in slope-intercept form using the following points:
(3 , 4) and (0 , 7)
y = -1x + 7
400
What is the slope from this equation?
What is the coordinate (x, y) from this equation?
y + 6 = -5(x - 1)
Slope: m = -5
Coordinate: (1, -6)
400
Layla wants to go take her friends to a music festival and she has a total of 150 dollars to spend. Regular admission tickets, x, cost $6 and VIP tickets, y, cost $30.
Represent this situation with a Standard Form equation.
6x + 30y = 150
400
The graph shows a proportional relationship. Create a direct variation equation to represent the line.
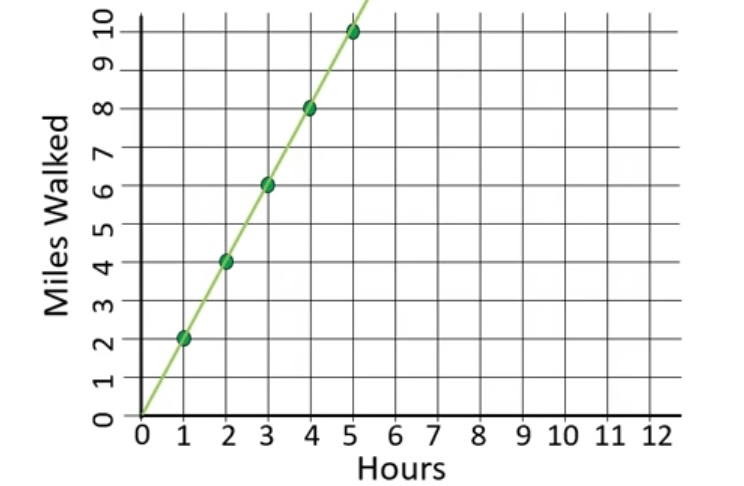
y = 2x
500
Find the slope of the line that includes the points listed in the table.
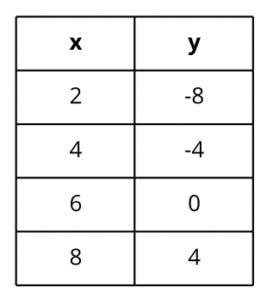
4/2 or 2/1 or 2
500
Cleo is planning a girl scout's trip and is selling chocolate bars to raise money. The price of each chocolate bar is $8, and she starts with an initial donation of $50 from a sponsor. The total amount of money Cleo raises, y, depends on the number of chocolate bars sold, x.
Write the equation in Slope-Intercept form that represents the total amount of money Cleo raises based on the number of chocolate bars sold.
y = 8x + 50
500
Write an equation in Point-Slope form that passes through the two points (-1, 3) and (-2, 5).
Use the SECOND POINT to write Point-Slope form.
y - 5 = -2(x + 2)
500
Rewrite the following equation from standard form to slope-intercept form:
-5y - 15x = 90
y = -3x - 18
500
The relationship in the graph is proportional. Write a direct variation equation to represent the line.
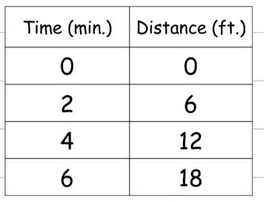
y = 6/2x OR y = 3x
600
Find the slope of the line that includes the following points. (4, -5) (-4, 5)
-10/8 which simplifies to -5/4
600
The equation y = -5x + 50 represents the height of a ball, y (in feet), after x seconds.
Interpret the y-intercept using the context of the problem.
(0, 50)
At 0 seconds, the ball is 50 feet high.
600
Convert the following equation to slope-intercept form:
y - 6 = 1/2(x + 16)
y = 1/2x + 14
600
Leah has $60 and wants to buy some different kinds of dried fruit. Apricots, x, cost $15 per pound and Mangos, y, cost $12 per pound.
The situation is represented with the Standard Form equation 15x + 12y = 60.
If Leah bought 2 pounds of Apricots, how many pounds of Mangos could she buy?
2.5 lbs of Mangos
600
Micah is going on a walk. The relationship between how many miles she walks, y, and the hours she has been walking, x, is represented by the following equation.
y = 2.5x
Interpret the slope using the context of the problem.
For every one hour she walks, she can go 2.5 miles.