Arithmetic Sequences
Piecewise Functions
Linear Systems
Graphs!
Graph Transformations
100
This term describes a sequence where each term after the first is the sum of the previous term and a constant.
a. Geometric Sequence
b. Fibonacci Sequence
c. Arithmetic Sequence
d. Harmonic Sequence
c. Arithmetic Sequence
100
What characteristic differentiates piecewise functions from other types of functions?
a. Continuous graph
b. Defined by a single equation
c. Defined by multiple equations over different parts of the domain
d. Only defined for positive numbers
c. Defined by multiple equations over different parts of the domain
100
What are the 3 types of solutions that could be found when solving two equation systems?
One solution, Zero solutions, Infinite (many) solutions
100
When finding the solution of this inequality 3x-1>4x+2 , what will the solution look like?
a) a point on a graph
b) there are no solutions, the lines are parallel
c) an inequality
d) a shaded region
c) an inequality
-3>x OR x<-3
100
On the board:
Describe the transformation of f(x) to g(x)
f(x) was shifted UP 3 units and RIGHT 4 units
200
The common difference in the arithmetic sequence 3, 7, 11, 15,... is this number.
What is 4.
200
In a piecewise function, this part determines which sub-function to use based on the input value.
a.Parameter
b.Domain
c.Range
d.Condition
b.Domain
200
This method involves adding or subtracting equations to eliminate one variable in a system of equations.
Solving by elimination
200
What is the interval where this graph is negative?
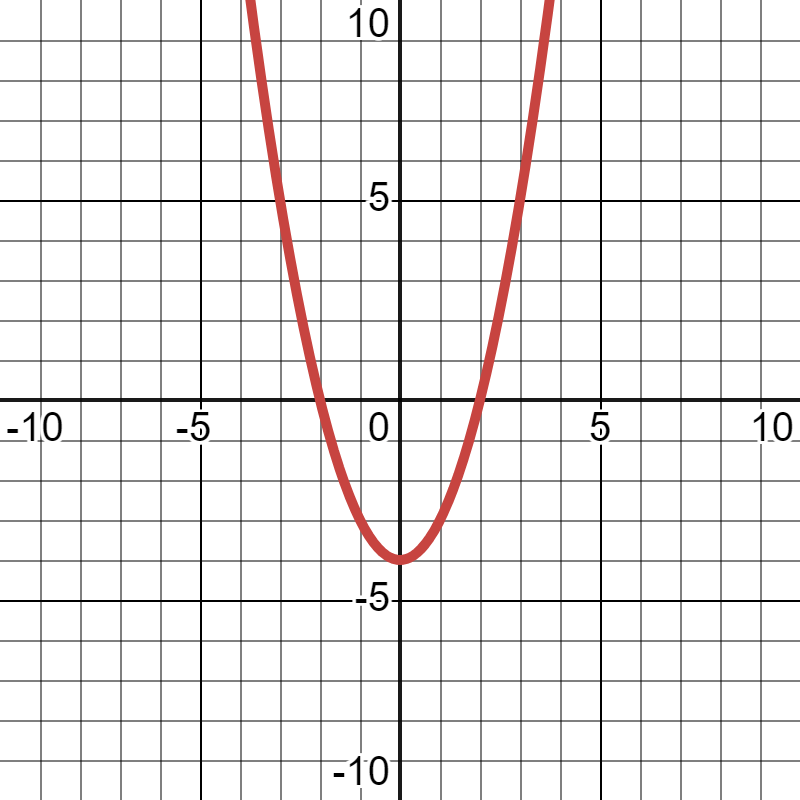
-2<x<2 OR (-2,2)
200
What is the effect of replacing ( f(x) ) with ( f(x) + k ) on the graph of the function?
a. Horizontal shift left by ( k ) units
b. Vertical shift up by ( k ) units
c. Horizontal shift right by ( k ) units
d. Vertical shift down by ( k ) units
b. Vertical shift up by ( k ) units
300
This formula gives the nth term of an arithmetic sequence explicitly.
a. a_n = a_1 + (n-1)d
b. a_n = a_1 \cdot r^{n-1}
c. a_n = a_{n-1} + d
d. a_n = \frac{a_1 + a_n}{2}
a_n = a_1 + (n-1)d
300
Given the piecewise function below. What is g(3)?
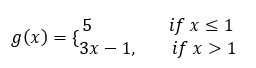
What is 8?
300
In the system of equations 2x + 3y = 6 and 4x - y = 5, this is the value of x after solving.
x=3/2 (y=1)
300
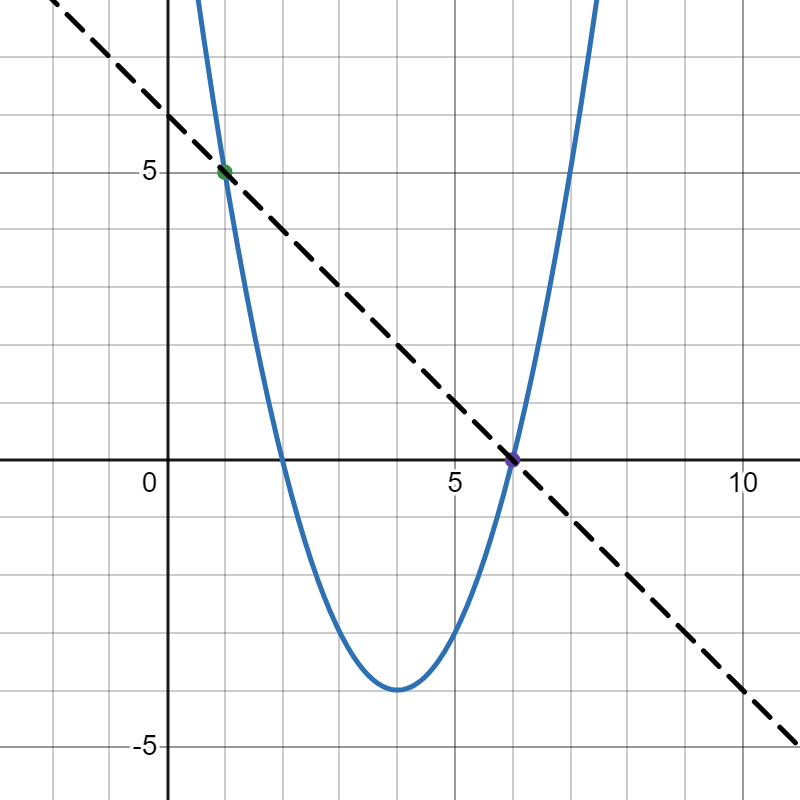
What are the x-intercepts of this graph?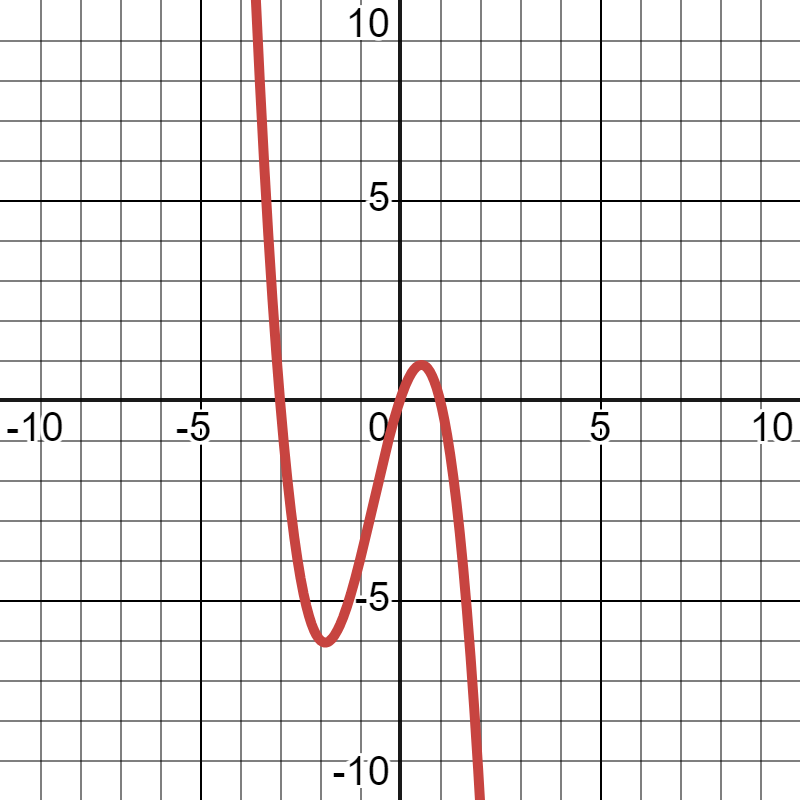
(-3,0) and (0,0) and (1,0)
300
If a function is reflected across the x-axis, which transformation has occurred?
a. ( f(x) \to -f(x) )
b. ( f(x) \to f(-x) )
c. ( f(x) \to f(x) + 2 )
d. ( f(x) \to f(x) - 2 )
a. ( f(x) \to -f(x) )
400
In an arithmetic sequence, if a_1 = 5 and d = 3 , this is the 4th term.
What is 14?
400
What is the piecewise function definition of f(x)=|x|?
400
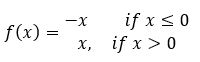
What is the solution to the system x + y = 10 and 2x - y = 2?
What is (4,6)?
400
What is the rate of change over (1,6)?
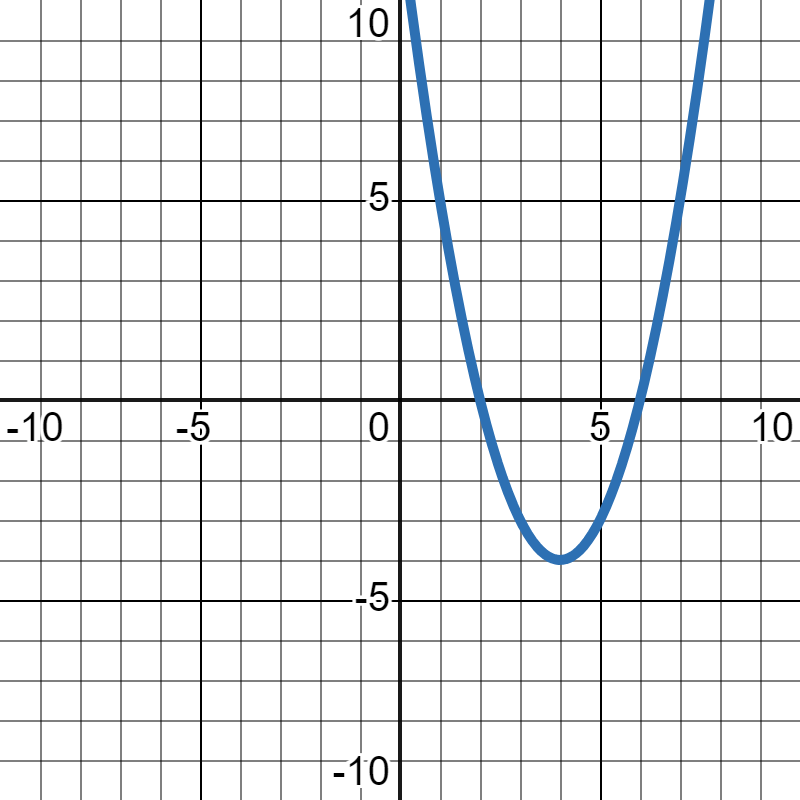
The rate of change is -1 [-5/5]
Do this by finding the slope of this line
400
What does the transformation ( f(x) \to 2f(x) ) do to the graph of ( f(x) )?
Stretches vertically by a factor of 2
500
This is the sum of the first 10 terms of the arithmetic sequence 1, 3, 5, 7,...
What is 100?
500
On the board:
What is the piecewise equation for the graph?
500
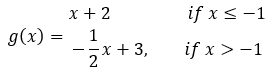
In the system 3x + 4y = 12 and 6x + 8y = 24, the lines are considered to be this.
a. Parallel
b. Perpendicular
c. Overlapping lines
d. Intersecting
c. Overlapping lines
500
Which region will this systems of inequalities highlight?
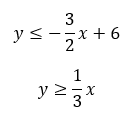
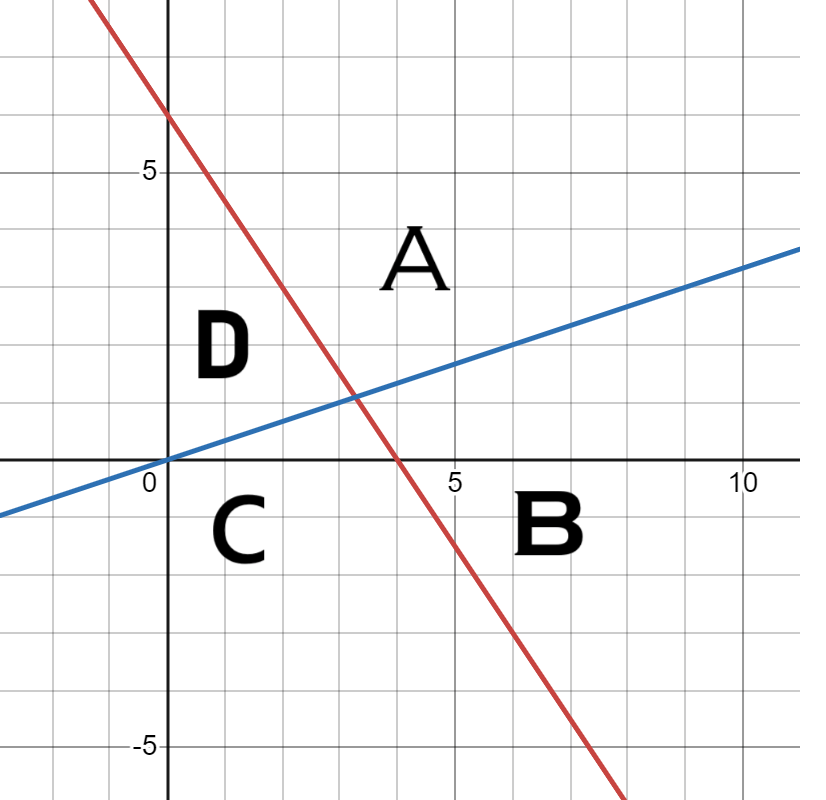
D
500
What is the result of the transformation ( f(x) \to f(x + 5) )?
Horizontal shift left by 5 units