Point-Slope Form
1-variable Inequalities
2-Variable Inequalities
Parallel & Perpendicular Lines
100
Write the equation of the line with a slope of -2 that passes through the point (-3, 4). Write the equation in point-slope form.
y - 4 = -2(x + 3)
100
State the inequality described in the graph below:
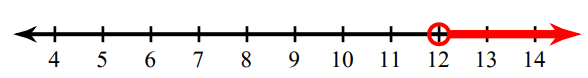
x > 12 or 12<x
100
Tell whether the ordered pair is a solution of the given inequality: x − y ≤ 0; (5, 2)
FALSE!
5 - 2 is NOT less than or equal to 0.
100
Find the slope of any line that is perpendicular to the line between the two given points: (2, 1) and (4, 5)
m of the line = 2
m perpendicular = -1/2
200
Write the equation of the line that passes through the points (-3, 5) and (5, 1).
y - 1 = -1/2 (x - 5)
y - 5 = -1/2 (x + 3)
200
State the simplest form of the inequality shown in the graph below.
x < -10 or x > - 9
200
graph the inequality in a coordinate plane: x > 6
(Show your graph. Must have dotted line and shade to the right of the vertical line)
200
Are the two given lines parallel, perpendicular or neither? State why.
x + 3y = 6
y = 3x - 5
Perpendicular:
1st line's slope is -1/3 which is the opposite reciprocal of 3.
300
Convert the equation to point-slope form using the y-intercept as your point:
2x - 3y = 6
y-int: (0, -2); m = 2/3
y + 2 = 2/3(x - 0)
300
Solve and sketch a graph:
-64 < 6x - 4 <=-22
-10<x<=-3
300
Describe and correct the error in graphing the inequality.
y < −x + 1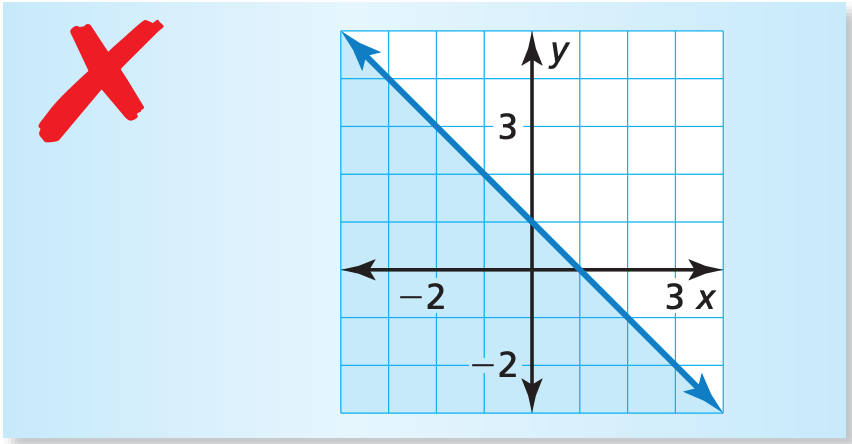
Less than or equal to!
300
Write the equation of the line that is parallel to the given line and passes through the given point.
2x - 3y = 6; (-6, 2)
m = 2/3
y - 2 = 2/3 ( x + 6) OR y =2/3 x + 6
400
Convert the equation to point-slope form using the x-intercept:
y = 1/2x - 4
y - 0 = 1/2 (x - 8)
400
Solve for x and graph the solution on the number line below. State the solution in simplest form.
x+3<−2 or x + 3 < 6
x <3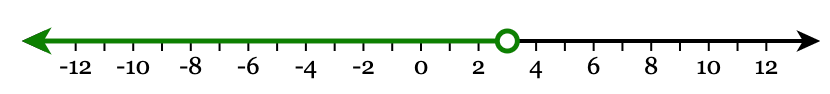
400
Write an inequality that represents
the graph.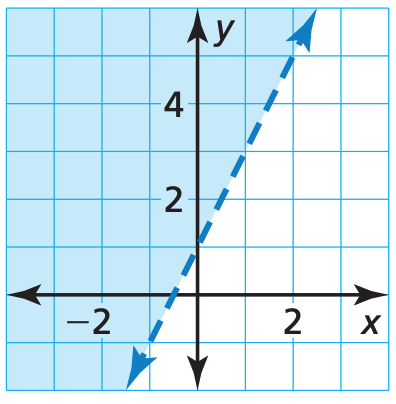
y > 2x + 1
400
Find the equation, in standard form, of the line passing through the point (12, -1)and perpendicular to 3x - 5y = 25
m of the given line = 3/5
m perpendicular = -5/3
y + 1 = -5/3(x - 12)
5/3x + y = 19
5x + 3y = 57
500
Derive point-slope form.
m = (y2 - y1) / (x2-x1)
m(x2 - x1) = y2 - y1
y - y1 = m(x-x1)
500
Solve the inequality and graph the solution.
16>=4x + 4 AND 36 <= 4x + 4
No Solution
500
Large boxes weigh 75 pounds, and small boxes weigh 40 pounds. The weight limit on a crane is 2,000 lbs. Write an inequality to describe how many of each type of box the crane can hold. State a realistic domain and range for the inequality. Assign x to be large boxes and y to be small boxes.
75x + 40 y <=2000
The values can only be positive integers so you need to find the intercepts. X intercept: (26.6..., 0) & y-intercept: (0, 50)
Domain:
0<=x<= 26
Range:
0<=y <=50
500
Is the triangle with vertices (-2, 3) , (3, 3) and (2, 1) a right triangle?
Slopes:
m1 = 0
m2 = 2
m3 = -2/4 = -1/2
YES!