In a perfect linear model, all the data points will make what shape?
A straight line
The equation for a line of best fit is y = 3.79 + 2.5x. What is the slope of this line?
2.5
A store's sales are predicted by the model Sales = 8,106 + 91.34(Staff). What are the predicted sales if there is 1 staff?
8,197
Describe the strength and direction of a correlation of -0.9.
Strong negative
What does a positive residual mean about a data point?
The observed value is greater than the predicted value.
The equation for a line of best fit is y = -17.05x + 32.1. What is the y-intercept of this line?
32.1
A store's sales are predicted by the model Sales = 8,106 + 91.34(Staff). With 14 people working, what would you expect sales to be?
9,384.76
Describe the strength and direction of a correlation of 0.14.
No correlation (Correlation < 0.3 is not considered meaningful)
With an observed value of 25 and a predicted value of 45, what is the residual?
-20
A store's sales are predicted by the model Sales = 8,106 + 91.34(Staff). What does the y-intercept mean in the context of this problem?
The store will sell $8,106 with no staff
A store's sales are predicted by the model Sales = 8,106 + 91.34(Staff). Should we predict that the store will sell $7,761 with -4 staff? EXPLAIN
No. -4 staff is impossible.
Joseph says, "There is a strong correlation of 1.22 between Sugar and Fat content." What is Joseph's mistake?
Correlation is between -1 and +1.
Is this dataset a good candidate for a linear model? EXPLAIN.
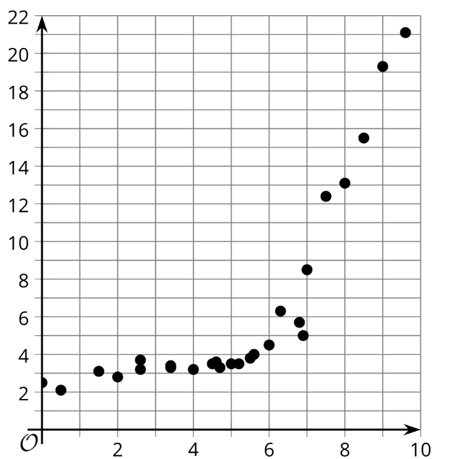
NO because the data does not approximate a straight line
A store's sales are predicted by the model Sales = 8,106 + 91.34(Staff). What does the slope mean in the context of this problem?
For each additional staff member, the store sells $91.34 more.
A store's sales are predicted by the model Sales = 8,106 + 91.34(Staff). The store sold $9,000 today. How many staff were likely to be working?
9.8 (rounds to 10)
Give an example of two variables that are correlated where one does NOT cause the other.
(Various)
Explain what is wrong with this line of best fit:
y=-1.27x^2+3.07x+5.19
It's a parabola, not a line
Give an example of a regression line where the y-intercept does NOT make sense. Describe the x and the y variables.
Any situation where x = 0 does not make sense in the problem.
A store's sales are predicted by the model Sales = 8,106 + 91.34(Staff). Two people are working and the store sells $8,600. What is the residual?
$311.32
What do we call a strong correlation that has no meaning or basis in reality?
Spurious