Linear Equations
Linear Models
Direct Variation (Proportion)
100
What is the gradient of the line 2x+3y+4=0?
-2/3
100
Conversion graphs can be used to convert from one currency to another.
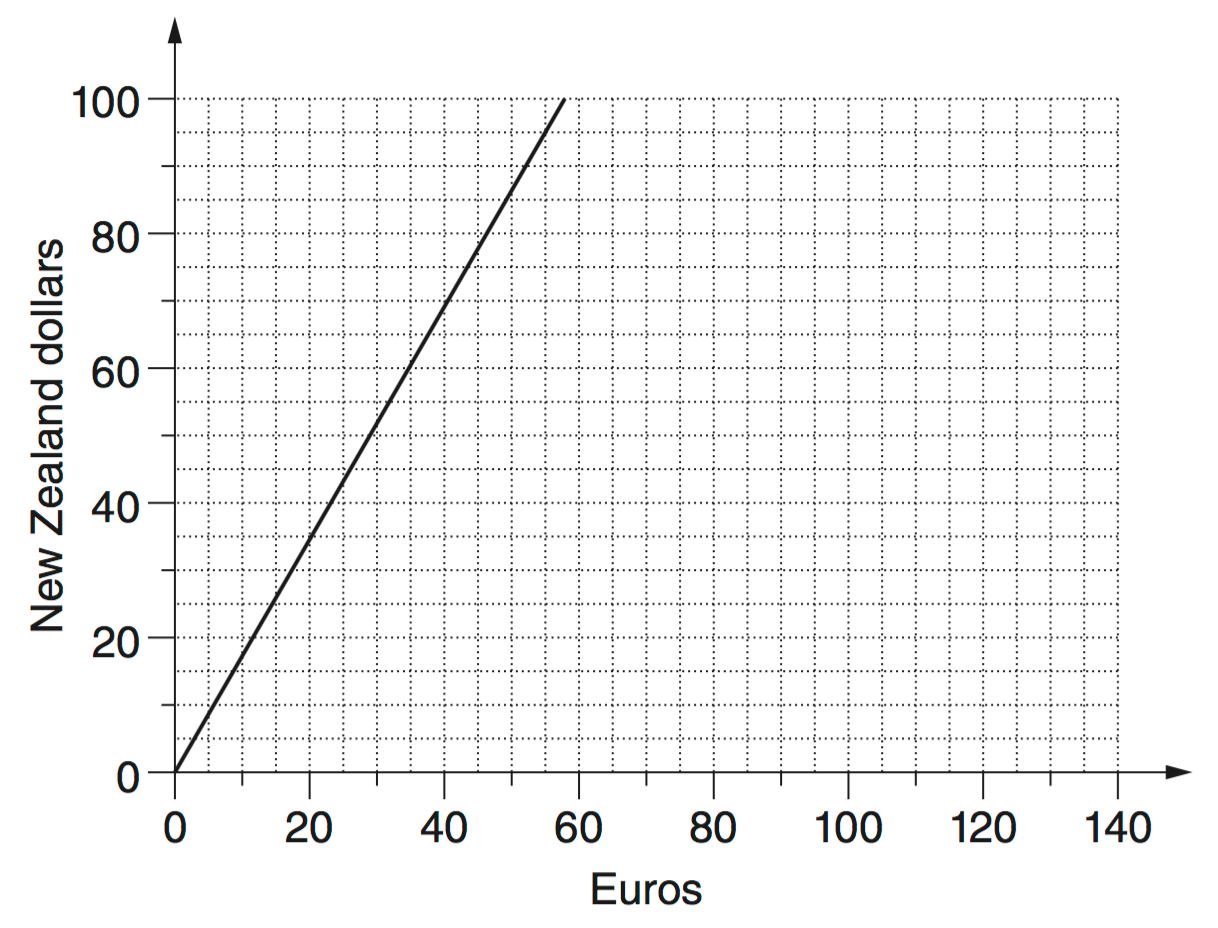
Sarah converted 60 Australian dollars into Euros. She then converted all of these Euros
into New Zealand dollars.
How much money, in New Zealand dollars, should Sarah have?
$60 Australian = 46 Euro
46 Euro =$78 New Zealand
100
The circumference of a circle (C) varies directly with the diameter of the circle (d) using the formula
C = pid
What is the constant of variation?
pi
200
What is the x-intercept of the line x+3y+6=0?
(– 6, 0)
200
The fuel consumption for a car is 6.7 litres/100 km. On a road trip, the car travels a distance of 1560 km and the fuel cost is $1.45 per litre.
What is the total fuel cost for the trip?
$151.55
200
The weight of an object on the moon varies directly with its weight on Earth. An astronaut who weighs 84 kg on Earth weighs only 14 kg on the moon.
A lunar landing craft weighs 2449 kg when on the moon. Calculate the weight of this landing craft when on Earth.
14 694 kg
300
Renee went bike riding on a holiday.
The hiring charges are listed in the table below:
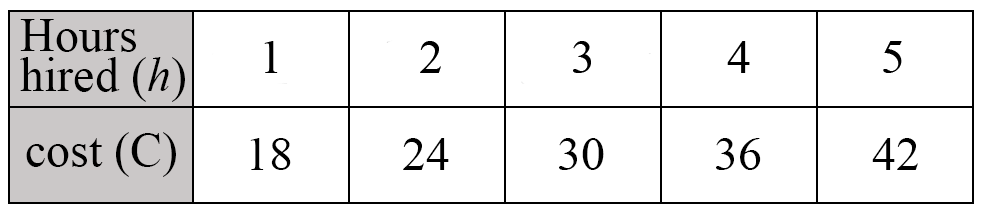
Write an equation which shows the relationship between C and h.
C=12+6h
300
Heather’s car uses fuel at the rate of 6.6 L per 100 km for long-distance driving and 8.9 L per 100 km for short-distance driving.
She used the car to make a journey of 560 km, which included 65 km of short-distance driving.
Approximately how much fuel did Heather’s car use on the journey?
38.455 L
300
The weight of a bundle of A4 paper (W kg) varies directly with the number of sheets (N) of A4 paper that the bundle contains.
This relationship is modelled by the formula W=kN, where k is a constant.
The weight of a bundle containing 500 sheets of A4 paper is 2.5 kilograms.
A bundle of A4 paper has a weight of 1.2 kilograms. Calculate the number of sheets of A4 paper in the bundle.
240 sheets
400
What is the equation of the line l?
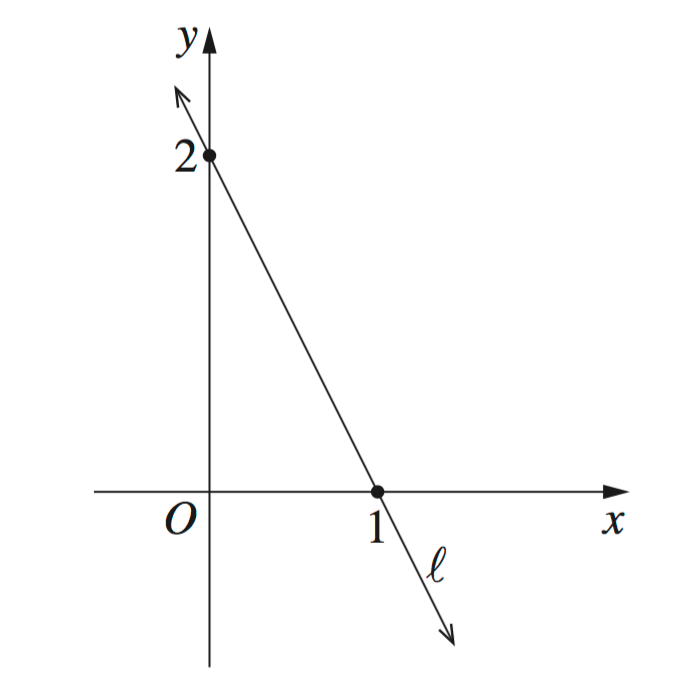
y=−2x+2
400
Sandy travels to Europe via the USA. She uses this graph to calculate her currency conversions.
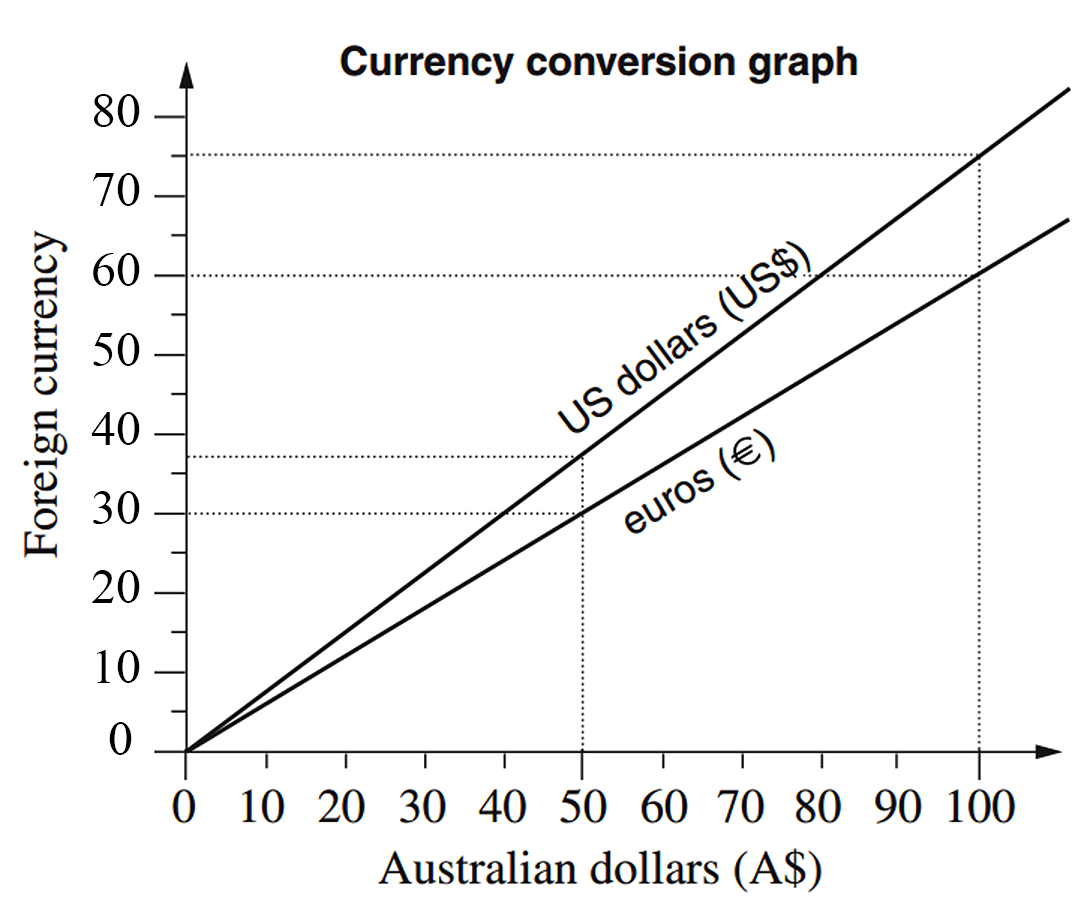
After leaving the USA she has US$150 to add to the A$600 that she plans to spend in Europe.
She converts all of her money to euros. How many euros does she have to spend in Europe?
480 €
400
The relationship between British pounds (p) and Australian dollars (d) on a particular day is shown in the graph.
Write the direct variation equation relating British pounds to Australian dollars in the form p=md. Leave m as a fraction.
p=4/7d
500
Chris started to make this pattern of shapes using matchsticks.
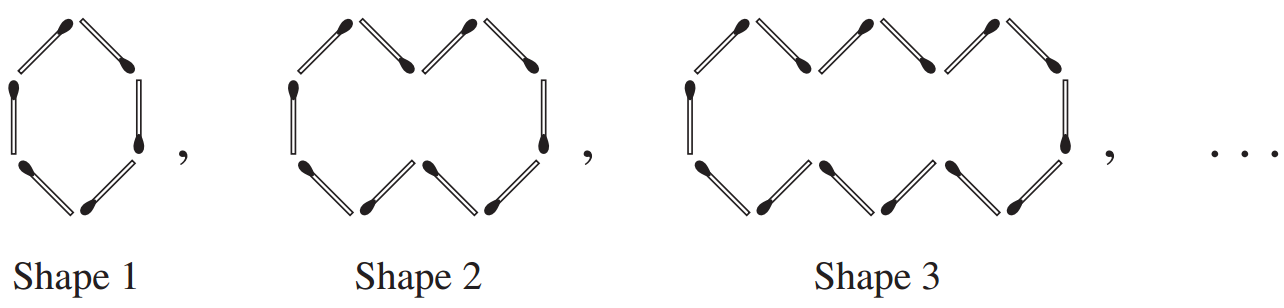
If the pattern of shapes is continued, which shape would use exactly 486 matchsticks?
Shape 121
500
John knows that
• one Australian dollar is worth 0.62 euros
• one Vistabella dollar ($V) is worth 1.44 euros.
John changes 25 Australian dollars to Vistabella dollars.
How many Vistabella dollars will he get?
25 AUD = 15.5 Euros = $V10.76
500
The weight of a steel beam, w, varies directly with its length, ℓ.
A 1200 mm steel beam weighs 144 kg.
Calculate the weight of a 750 mm steel beam.
90 kg