Identify as linear or exponential. Then write the function formula.
A school has 2000 students. They add 40 more each month.
Linear
y=40x+2000
Identify as linear or exponential. Then write the function formula.
A prepaid phone is loaded with 100 dollars. Each minute you use cost 0.20.
Linear
y=-0.20x+100
Write an exponential growth model for the situation.
You make 40,000 per year for a job that increases your salary by 2% per year
y=40,000(1+0.02)^t
Write an exponential decay model for the situation.
A 45,000 dollar car depreciates 33% each year
y=45,000(1-0.33)^t
x^6 *x^3
x^9
Identify as linear or exponential. Then write the function formula.
Mr. Guzman has created 40,000 math assignments. Each year he creates 500 more.
Linear
y=500x+40,000
Identify as linear or exponential. Then write the function formula.
Disney land passes cost 1,000 for the year. You go every week and spend 200 on drinks, food, and souvenirs.
Linear
y=200x+1000
Write an exponential growth model for the situation.
A business profits 100,000 per year. Each year the profit increases by 44%
Y=100,000(1+0.44)^t
Write an exponential decay model for the situation.
A stock is valued at 15,000 dollars. Each year the value decreases by 4%
y=15,000(1-0.04)^t
(x^3)^5
x^15
Identify as linear or exponential. Then write the function formula.
A group of students invest 100 dollars into a savings account. Each month the money is doubled.
Exponential
f(x)= 100(2)^x
Identify as linear or exponential. Then write the function formula.
There are 50,000 tigers left in the wild. Every five years the number of tigers left are halved.
Exponential
f(x) = 50,000(1/2)^x
Write an exponential growth model for the situation.
You deposit 500 dollars into an account that pays 7.8% interest compounded yearly.
y=500(1+0.078)^t
Write an exponential decay model for the situation.
You buy a new iPhone for 1,200 dollars. Each year the value decreases by 2.5%
y=1,200(1-0.025)^t
(-2y^5)(-9y^3)
18y^8
Identify as linear or exponential. Then write the function formula.
x: 0 1 2 3 4 5
y:20 25 30 35 40 45
Linear
y=5x+20
The function f(x)=20x+500 represents a deposit on a new car plus gas per week. Find f(10) or how much you have paid in 10 weeks
f(10)=20(10)+500
f(10) = 200+500
f(10)= 700
Identify the initial amount and growth rate.
y=33.5(4.75)^t
Initial amount = 33.5
growth rate = 4.75-1= 3.75
Identify the initial amount and decay rate for the following.
y=185(0.23)^t
Initial amount = 185
Decay rate= 1-0.23=0.77
Decay rate = 0.77
(-4x^4)^3
-64x^12
Identify as linear or exponential. Then write the function formula.
x 0 1 2 3 4
y: 50 35 24.5 17.15 12.005
Exponential
f(x) = 50(35/50)^x
f(x) = 50 (0.7)^x
Consider the function f(x)=10(4)^x. What is the value of f(4)?
f(4) = 10(4)^(4)
f(4) = 10(256)
f(4)= 2560
A population of 1,000,000 increases by 15% each year. What is the total population after 8 years?
Round to the nearest hundredth.
y=1,000,000(1+0.15)^8
y= 3,059,022.86
Zombies take over the world. Currently 5,000,000 people are infected, but you find a cure that declines the zombie population by 3% each month. How many zombies are left after 2 years?
Round to the nearest hundredth.
y=5,000,000 (1-0.03)^t
2 years = 24 months
y= 5,000,000 (0.97)^24
y=2,407,086.11
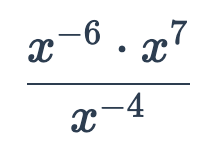
x^5