Loan Amortization
Single-Payment Loans
Down Payments & Financing
Installment Loans - Using a Table
Early Payoff & Interest Savings
100
A $6,000 loan at 6% APR for 36 months has a monthly payment of $182.48. Find the interest and principal for the first payment.
1st interest = 6,000×0.06/12 = $30.00; Principal = 182.48−30.00 = $152.48; New Bal = $5,847.52
100
Lily Grant borrowed $1,800 for 60 days at 5% exact interest. What is the maturity value of the loan?
Interest = 1,800 × 0.05 × (60/365) = $14.79 → Maturity = $1,814.79
100
Sarah bought a refrigerator for $850 and made a 10% down payment. How much did she finance?
Down = 850×0.10=$85 → Financed = $765
100
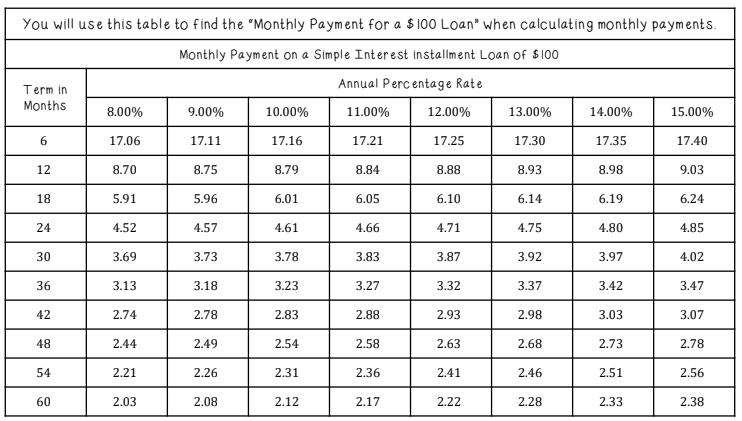
Ben Cooper borrowed $1,200 at 9% APR for 12 months. Using the table for “Monthly Payment per $100,” find the monthly payment and total cost.
Monthly = (1,200/100)×8.76 = $105.12; Total = $1,261.44; Finance = $61.44
100
A $4,000 loan at 10% APR for 24 months has a payment of $184.17. After 12 payments, balance is $2,100. How much interest is on the 13th payment?
Interest = 2,100×0.10/12 = $17.50
200
Carla owes $4,800 at 8% APR for 24 months with a payment of $217.16. How much of the first payment is interest?
Interest = 4,800×0.08/12 = $32.00; Principal = 185.16; New Bal = $4,614.84
200
Marcus Hall borrowed $2,450 for 90 days at 7% ordinary interest. What is the maturity value?
Interest = 2,450 × 0.07 × (90/360) = $42.88 → Maturity = $2,492.88
200
Kevin purchased a laptop for $1,250 and made a 15% down payment. What amount is financed?
Down = $187.50 → Financed = $1,062.50
200
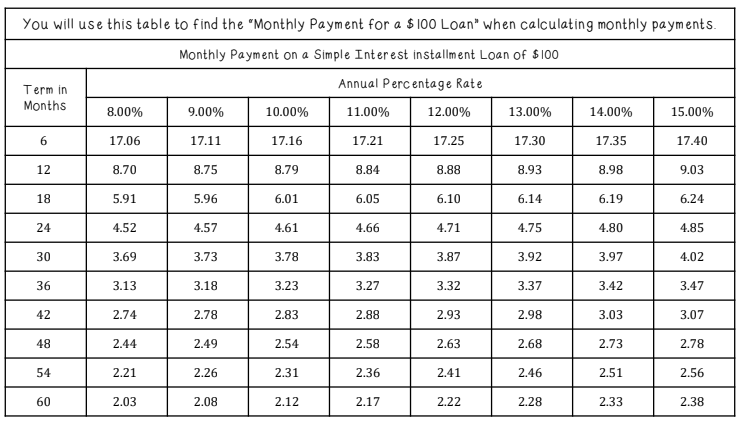
A $3,000 loan at 10% APR for 24 months. Use the table to find the finance charge.
Monthly = (3,000/100)×4.61 = $138.30; Total = $3,319.20; Finance = $319.20
200
A $7,800 loan at 8.5% APR for 36 months, monthly payment $246.19, balance after 15 payments is $4,100. What is the interest on the next payment?
Interest = 4,100×0.085/12 = $29.04
300
Dan owes $10,200 at 9% APR for 48 months with a monthly payment of $254.34. How much principal is paid in the first payment?
Interest = 10,200×0.09/12 = $76.50; Principal = 177.84; New Bal = $10,022.16
300
Tessa Collins took out a $3,200 single-payment loan for 120 days at 6.25% exact interest. What is the interest amount?
Interest = 3,200 × 0.0625 × (120/365) = $65.75
300
Dana is buying a car for $18,500 and paid 20% down. How much did she finance?
Down = $3,700 → Financed = $14,800
300
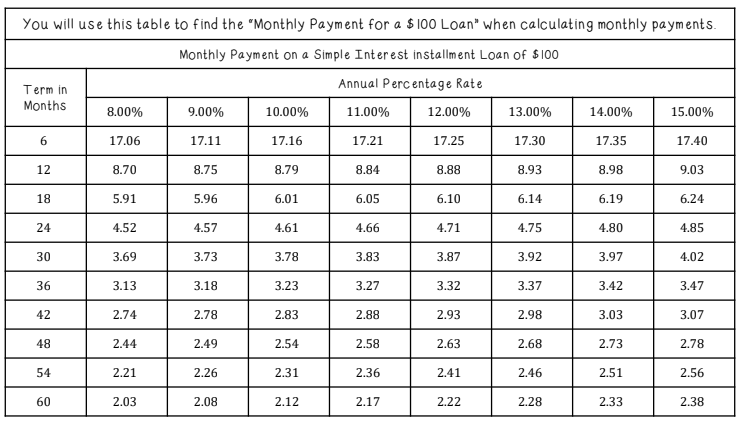
Chloe Grant borrowed $5,400 at 8% APR for 36 months. Find the total interest using the monthly payment table.
Monthly = (5,400/100)×3.13 = $169.02; Total = $6,084.72; Interest = $684.72
300
Nathan owes $6,500 at 9% APR for 48 months, payment $162.12. After 20 payments, balance is $3,800. If he pays off the loan, what is the payoff amount?
Interest = 3,800×0.09/12 = $28.50 → Payoff = $3,800 + $28.50 = $3,828.50
400
Sofia took out a $7,500 loan at 7.5% APR for 36 months with a payment of $233.14. What is the remaining balance after the first payment?
Interest = 7,500×0.075/12 = $46.88; Principal = 186.26; New Bal = $7,313.74
400
Owen Miller borrowed $4,600 for 150 days at 9% ordinary interest. Find the maturity value.
Interest = 4,600 × 0.09 × (150/360) = $172.50 → Maturity = $4,772.50
400
A motorcycle costs $9,200. If the buyer pays 12% down, what is the amount financed?
Down = $1,104 → Financed = $8,096
400
Raj Patel borrowed $9,800 at 7.5% APR for 48 months. Use the table to estimate the finance charge.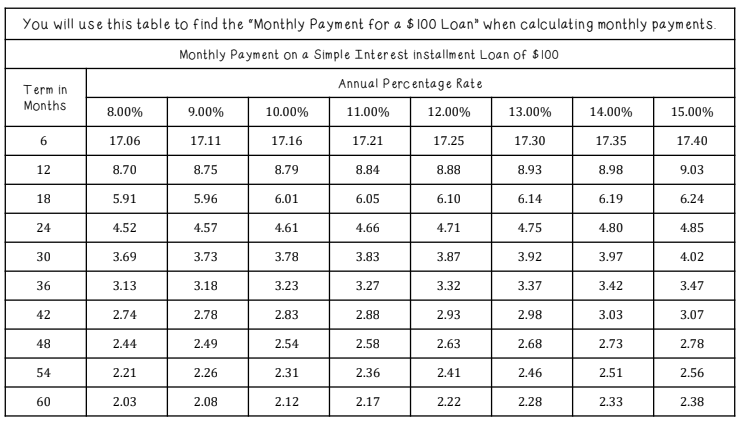 
Monthly = (9,800/100)×2.42 = $237.16; Total = $11,383.68; Finance = $1,583.68
400
A $9,000 loan at 10% APR for 60 months, payment $191.10. After 30 payments, balance is $5,100. How much interest is saved by paying it off now?
Interest = 5,100×0.10/12 = $42.50 → Payoff = $5,142.50 → Save ≈ $1,320 in future interest
500
Jared borrowed $9,250 at 6.75% APR for 48 months, monthly payment $219.52. Find the interest, principal, and new balance after the second payment.
1st interest = 52.03; principal = 167.49; new bal = 9,082.51; next interest = 51.73; new bal ≈ $8,915.02
500
Layla Ortiz borrowed $5,000 for 210 days at 8.75% exact interest. Find the interest and maturity value.
Interest = 5,000 × 0.0875 × (210/365) = $251.71 → Maturity = $5,251.71
500
A furniture set costs $4,680. If the down payment is $936, what percentage of the total price was the down payment?
% down = 936 ÷ 4,680 = 20%
500
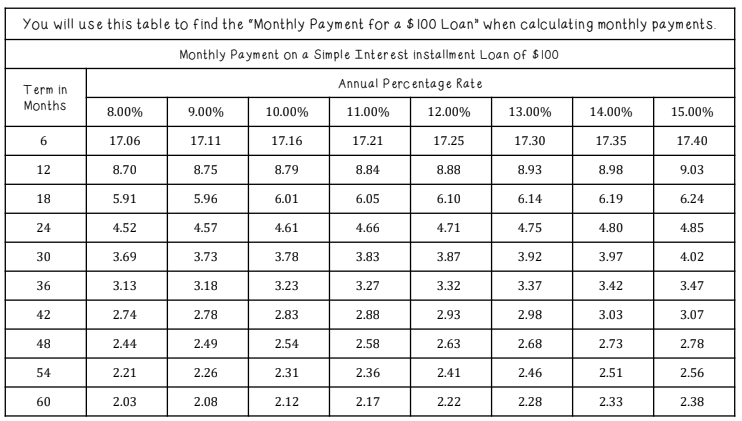
Andrea Kim borrowed $11,000 at 9% APR for 60 months. Using the table, determine the total of payments and finance charge.
Monthly = (11,000/100)×2.08 = $228.80; Total = $13,728.00; Finance = $2,728.00
500
Kendra owes $12,000 at 11% APR for 48 months, payment $310.78. After 18 payments, balance is $7,350. What is the interest on the next payment and interest saved if she pays off early?
Interest = 7,350×0.11/12 = $67.38 → Payoff = $7,417.38 → Save ≈ $1,560 interest