log2(8)
3
log3(13y)
log3(13) + log3(y)
log3(a) + log3(19)
log3(19a)
52x-1 = 57
x = 4
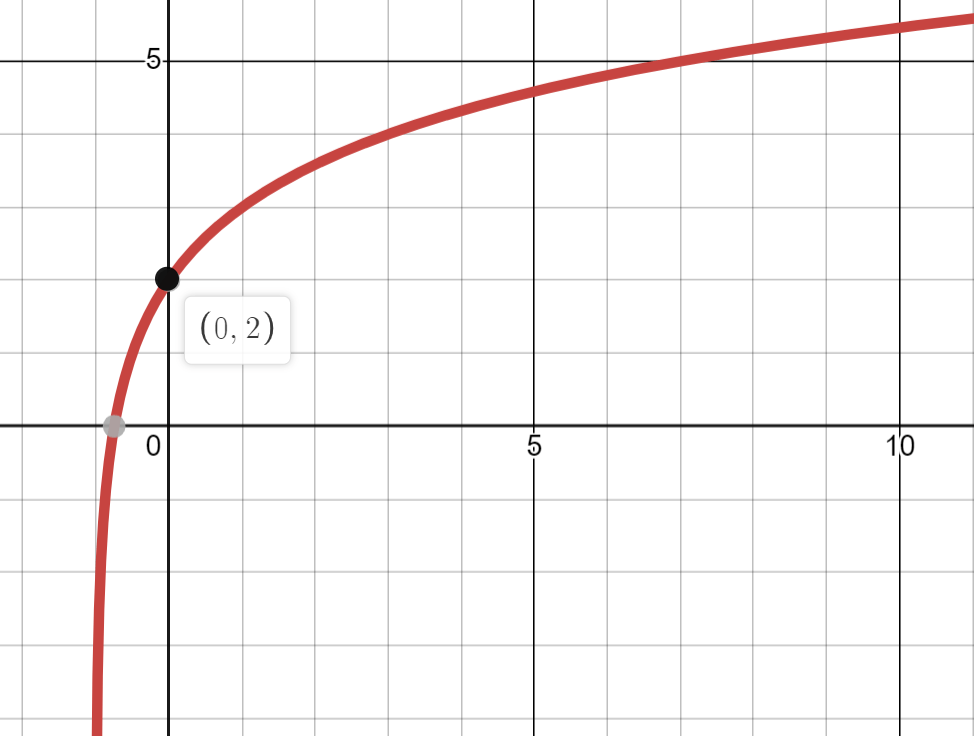
Parent graph: log2(x)
Write an equation with transformation: 2 units down
log2(x) - 2
log3(1)
0
log6(x2/y)
2log6(x) - log6(y)
log2(a) - log2(b)
log2(a/b)
log4(999) = x
4.982
Parent graph: log2(x)
Write an equation with transformation: 3 units to the right
log2(x-3)
log7(1/49)
-2
log(5a2b6)
log(5) + 2log(a) + 6log(b)
4log3(x) - 3log3(y)
log3(x4 / y3)
47x = 64x-2
x = - 3/2 or -1.5
Parent graph: log2(x)
Write an equation with transformation: 5 units left, 3 units down
log2(x+5) - 3
logx64 = 2
8
log2(3x2y3 / 10g3)
log2(3) + 2log2(x) + 3log2(y) - log2(10) - 3log2(g)
log5(x2) - 2log5(y) - log5(z)
log5(x2 / y2z)
5(3x)= 50
Include 3 decimal places
2.095
Where is the asymptote for the function:
log2(x - 2) - 3
x = 2
log64(x) = 2/3
1/9
log4(5x2y47 / 6z3)
log4(5) + 2log4(x) + log4(y) + 7log4(4) - log4(6) - 3log4(z)
log5(3) + 3log5(a) + 7log5(b) - log5(c)
log5(3a3b7 / c)
3 * (6^x)-10 = 80
1.898
What is the domain and range of the function:
log2(x + 3) - 250