Logaritmus

Exponenciální a logaritmický tvar

100

Přepište do exponenciálního tvaru:

  log₃81=4

 3⁴=81

200

Napište jako logaritmus:

  6^y=18

 log₆18=y

300

Přepište do exponenciálního tvaru:

  log_x7=2

 x²=7

400

Napište jako logaritmus:

  9^x=36

log₉36=x

500

Přepište do exponenciálního tvaru:

 log_12xy144=56

 12xy⁵⁶=144

Hodnota logaritmu - y

100

Vypočítej hodnotu logaritmu:

  log_7 343 

 3

200

Vypočítej hodnotu logaritmu:

  log_5 (1/25) 

-2

300

Vypočítej hodnotu logaritmu:

  log_2 1024 

10

400

Vypočítej hodnotu logaritmu:

 log_3 sqrt3 

1/2

500

Vypočítej hodnotu logaritmu:

 log_7 (-49) 

nelze

Základ logaritmu - a

100

Vypočítej základ logaritmu:

 log_a 16 =2

4

200

Vypočítej základ logaritmu:

 log_a 27 =1

27

300

Vypočítej základ logaritmu:

  log_a (1/64)=3

1/4

400

Vypočítej základ logaritmu:

 log_ a (1/32)=5 

1/2

500

Vypočítej základ logaritmu:

 log_a 125=-3 

1/5

Argument logartimu - x

100

Vypočítej x:

  log₄x=2

16

200

Vypočítej x:

log₃x=0

1

300

Vypočítej x:

log_(1/2) x=4

1/16

400

Vypočítej x:

log_(sqrt2) x=8

16

500

Vypočítej x:

log_(1/3) x=-4

81

Logaritmická funkce

100

Pro jaký základ, je logaritmická funkce klesající:

a in (0; 1)

200

Která z funkcí má základ 2?

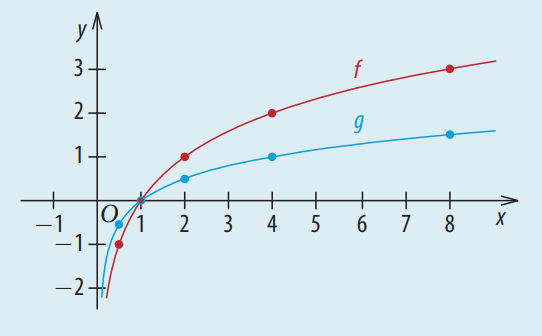
červená

300

Jaké číslo je základem přirozeného logaritmu ln?

e - Eulerovo číslo

Přibližná hodnota je 2,71828182846

400

Jaký graf je na obrázku?

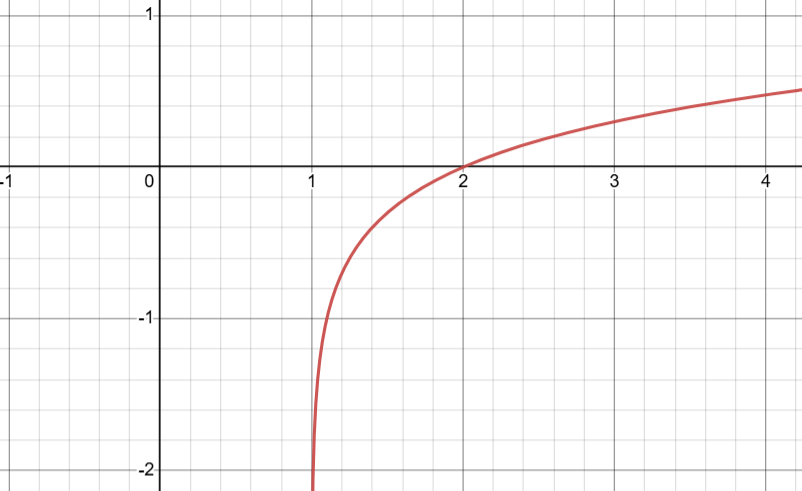
a: y= log₁₀(x-1)

b: y= log₁₀(x+1)

a: y= log₁₀(x-1)

500

Jaký graf je na obrázku?

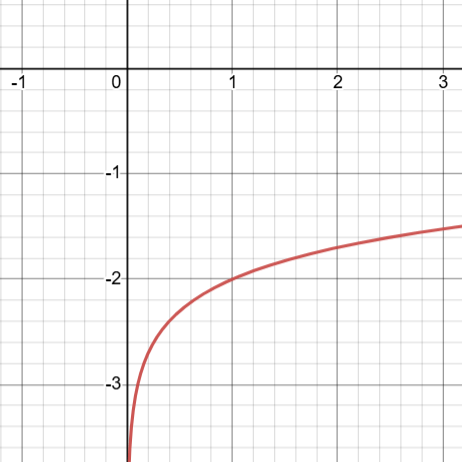
a: y= log₁₀(x) +2 

b: y= log₁₀(x) -2 

b: y= log₁₀(x) -2