Logarithms
Rationals
Sequences and Series
Trigonometry
Data Analysis
100
Rewrite in logarithmic form.
3^x=5
log_3 5=x
100
Determine whether the variables show direct variation, inverse variation, or neither. If they show direct or inverse variation, also write the equation.
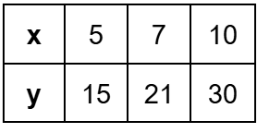
Direct.
y=3x
100
Give the 5th term for the arithmetic sequence
a_n=3+4n
a_5=3+4(5)=23
100
cos60^\circ
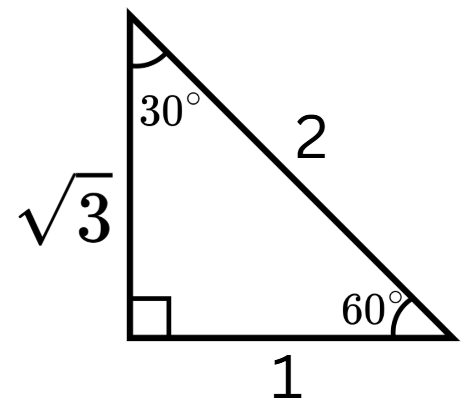
cos60^\circ=1/2
100
A normal distribution has a mean of 60 and a standard deviation of 5. What is the probability that a randomly selected x-value is greater than or equal to 60?
50%
200
Condense the logarithmic expression.
log_5x+2log_5z-log_5 y
=log_5x+log_5z^2-log_5y
=log_5xz^2-log_5y
=log_5({xz^2}/{y})
200
Solve the equation.
3/x=x-2
3/x=x-2
3=x^2-2x
0=x^2-2x-3
0=(x-3)(x+1)
x=3,-1
200
Write the formula for the sum of the first n terms of an arithmetic sequence.
S_n=n({a_1+a_n}/2)
200
sin45^\circ
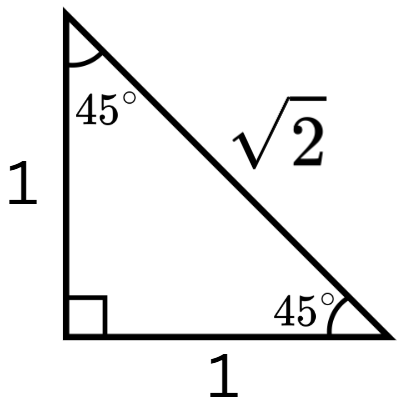
sin45^\circ=1/sqrt2=sqrt2/2
200
What percent of the area under the normal curve lies within 1 standard deviation of the mean?
68% by empirical rule
300
Simplify the expression.
sqrt{12x^6}
=sqrt12*sqrt{x^6}
=sqrt{4*3}*sqrt{(x^3)^2}
=2sqrt3*x^3
=2x^3sqrt3
300
Simplify the expression, if possible.
{x^2-4x+3}/{x^2+2x-15}
{(x-3)(x-1)}/{(x-3)(x+5)}
{x-1}/{x+5}, x!=3
300
Write the formula for the sum of the first n terms of a geometric series.
S_n=a_1({1-r^n}/{1-r})
300
Which of the six trigonometric functions are positive in Quadrant IV?
Cosine + Secant
300
A normal distribution has a mean of 70 and a standard deviation of 6. What is the probability that a randomly selected x-value is greater than 76, but less than 88?
13.5%+2.35%=15.85%
400
Solve for x.
log_2(3x+1)=2
2^{log_2(3x+1)}=2^2
3x+1=4
x=1
400
Find the sum.
3/{x+2}+4/{x^2+4x+4}
=3/{x+2}+4/{(x+2)(x+2)}
=3/{x+2}*{x+2}/{x+2}+4/{(x+2)(x+2)}
={3x+6+4}/{(x+2)(x+2)}
={3x+10}/{(x+2)(x+2)}
400
Evaluate the sum.
sum_{i=1}^\infty5(1/4)^{i-1}
S=a_1/{1-r}
=5/{1-1/4
=5/(3/4)
=20/3
400
cos(-210^\circ)
theta'=30^\circ
cos 30^\circ=sqrt3/2 .
Cosine is negative in Quadrant II.
cos(-210^\circ)=-sqrt3/2
400
A survey of 400 people gives a sample proportion of 35%. Given an interval that is likely to contain the true population proportion.
Margin of error =+-1/sqrtn=+-1/20=+-0.05 (or 5%)
35%+-5%->(30%,40%)
500
Solve for x.
8^{3x+1}=1/4
(2^3)^{3x+1}=2^-2
2^{9x+3)=2^-2
9x+3=-2
9x=-5
x=-5/9
500
Solve for x.
9/{x-2}+{6x}/{x+2}={9x^2}/{x^2-4}
LCD=(x+2)(x-2)
9(x+2)+6x(x-2)=9x^2
0=x^2+x-6
x=-3,2
x=-3
500
Write a recursive rule for the sequence.
5,11,17,23,...
a_1=5
a_n=a_{n-1}+6
500
Let sintheta=3/5 , and let
theta lie in Quadrant II. Evaluate cos and tan theta .
cos theta=-4/5
tan theta=-3/4
500
Ms. Nguyen claims that between 70% and 90% of students support replacing lunch time with math tutoring. Approximately how many students were surveyed?
Margin of error = 10% (or 0.10).
1/sqrtn=0.10->n=100