Translations of shapes
Rotation of shapes
Reflection of shapes
Dilation of shapes
Mixed Questions
100
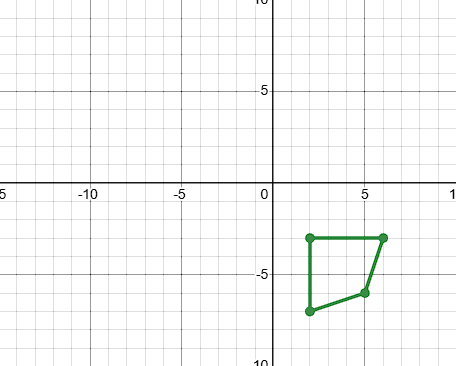
Translate the shape ABC 2 units down
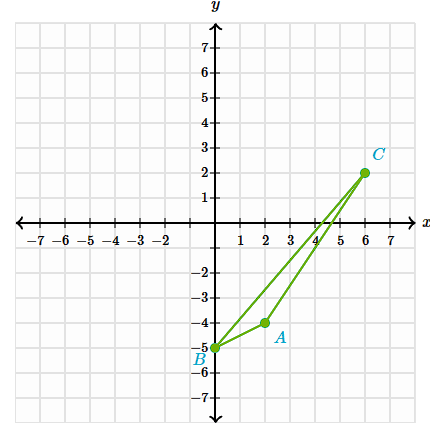
A2:(2, -6)
B2:(0, -7)
C2:(6, 0)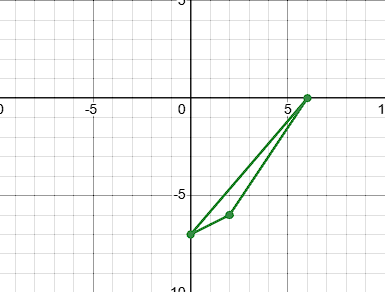
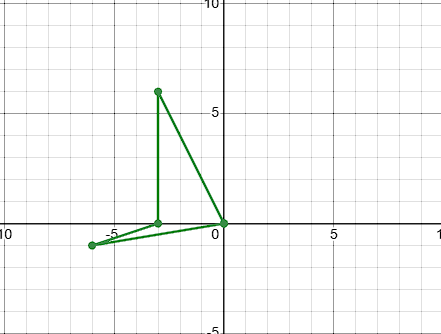
100
Rotate the shape TOP -180 degrees around the origin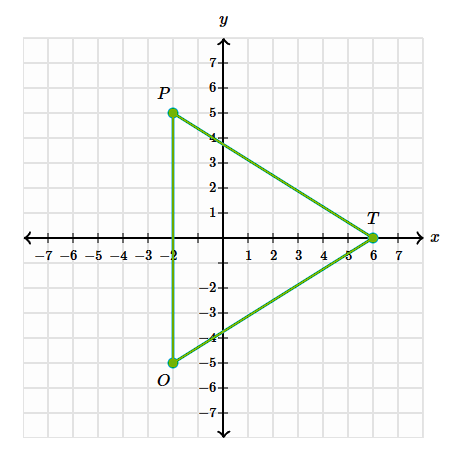
T':(-6, 0)
O':(2, 5)
P':(2, -5)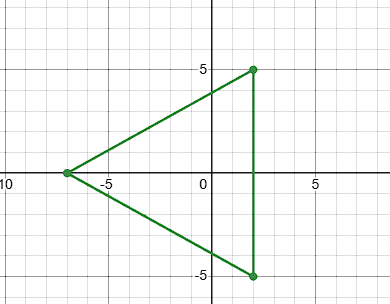
100
Reflect the shape ABC across the x-axis
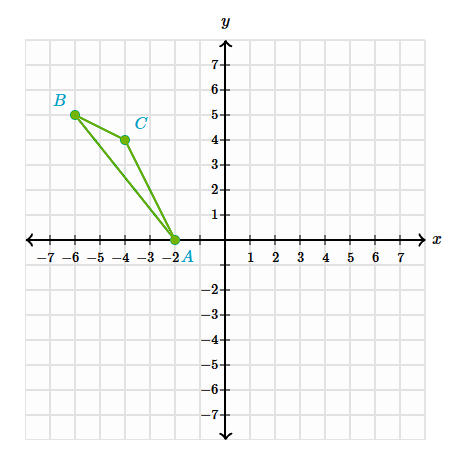
A':(-2, 0)
B':(-6, -5)
C':(-4, -4)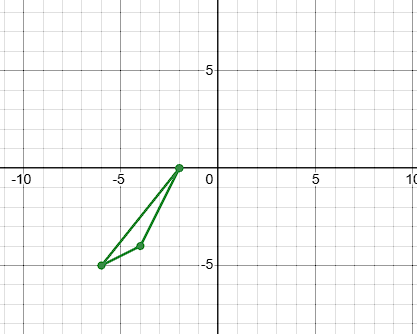
100
Find the length of the line segments under a scale of 4 with A as the center of dilation
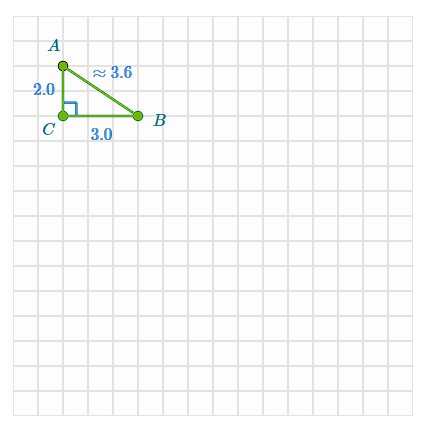
AB ≈ 11.4
BC = 12
CA = 8
100
Translate the shape ABC from (x, y) to (x +2, y +2)
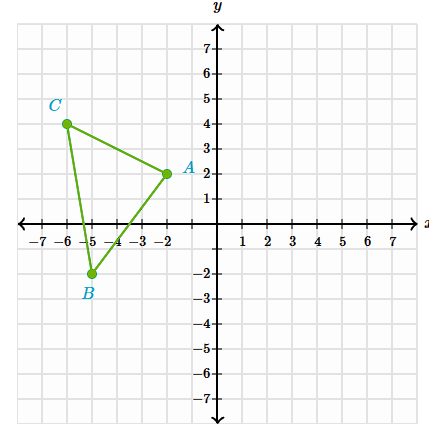
A:(0, 4)
B:(-3, 0)
C:(-6, 4)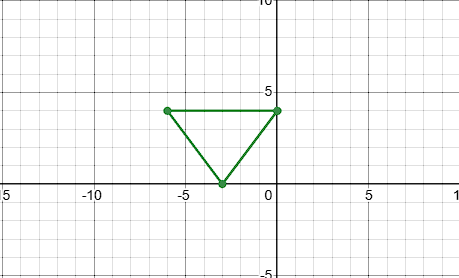
200
Translate the shape ABCD 2 units to the left and 3 units up
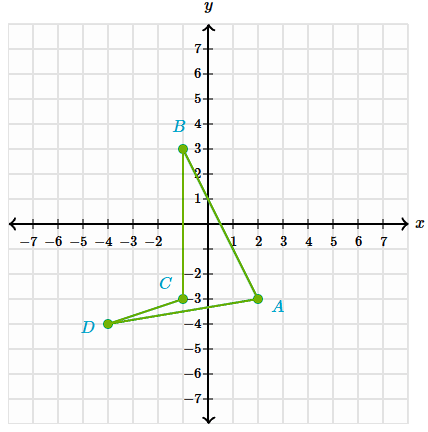
A2:(0, 0)
B2:(-3, 6)
C2:(-3, 0)
D2:(-6, -1)
200
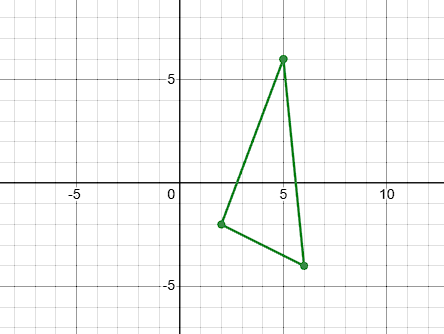
Rotate the shape EAR by 180 degrees around the origin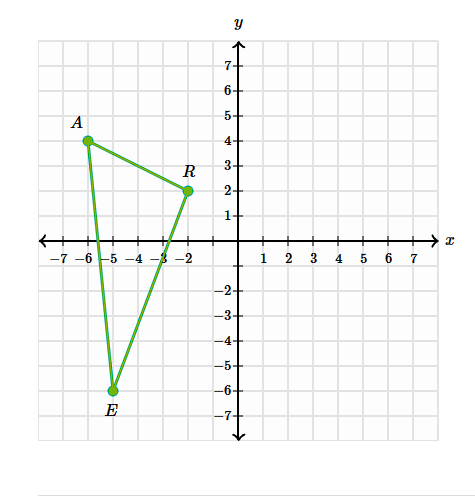
E':(5, 6)
A':(6, -4)
R':(2, -2)
200
Reflect the shape ABCD across the x-axis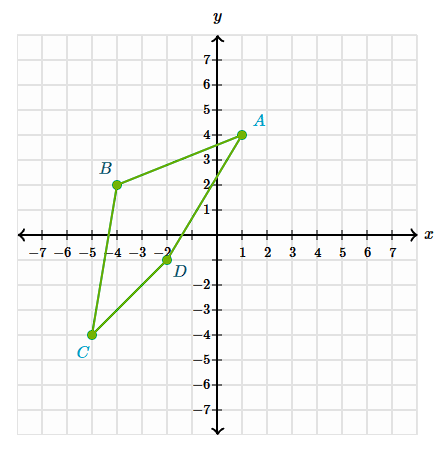
A':(1, -4)
B':(-4, -2)
C':(-5, 4)
D':(-2, 1)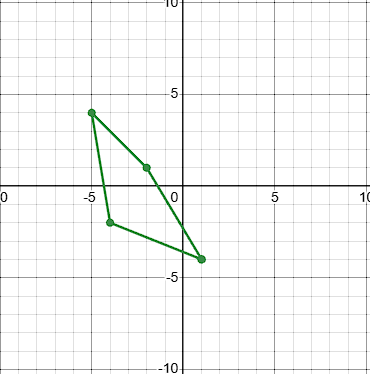
200
Find the length of the line segments under a scale of 4 with P as the center of dilation
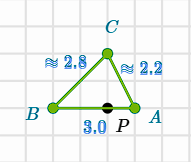
AB = 12
BC ≈ 11.2
CA ≈ 8.8
200
Find the length of the line segments under a scale of 1/2 with P as the center of dilation
AB ≈ 2.8
BC ≈ 6.1
CA ≈ 4.1
300
Translate the shape ABC from (x, y) to (x, y +3)
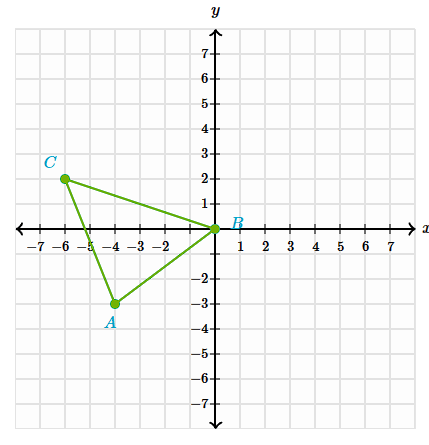
A2:(-4, 0)
B2:(0, 3)
C2:(-6, 5)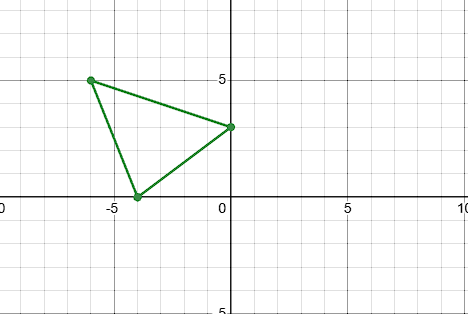
300
Rotate the shape TEAM by 180 degrees around the origin
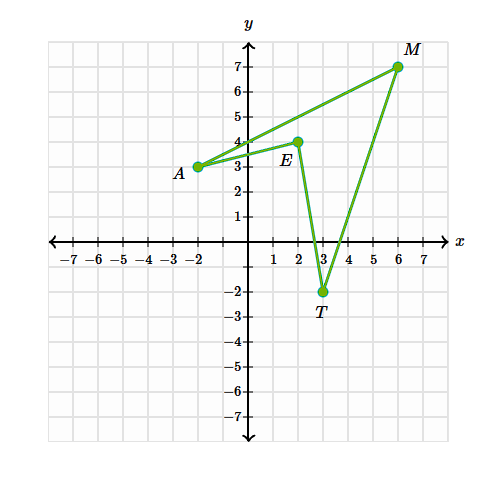
T':(-3, 2)
E':(-2, -4)
A':(2, -3)
M':(-6, -7)
300
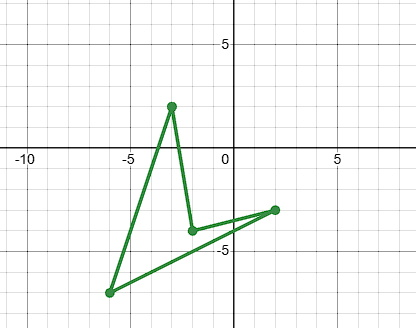
Reflect the shape ABCD across the y-axis
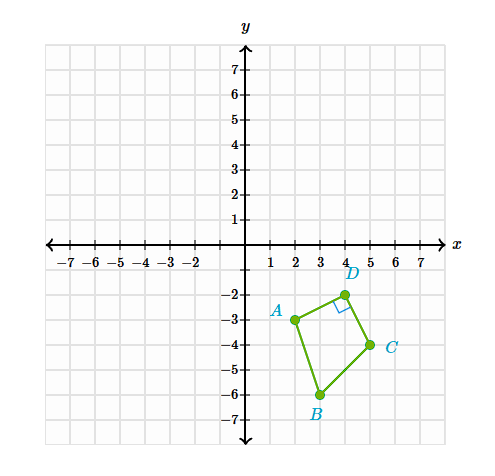
A':(-2, -3)
B':(-3, -6)
C':(-5, -4)
D':(-4, 2)
300
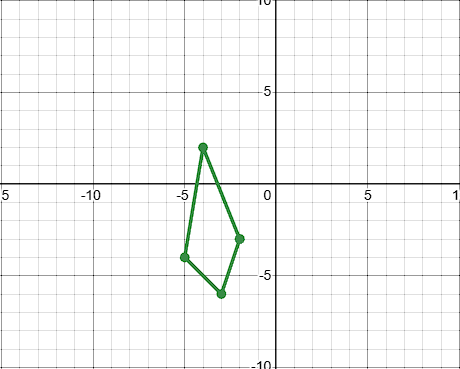
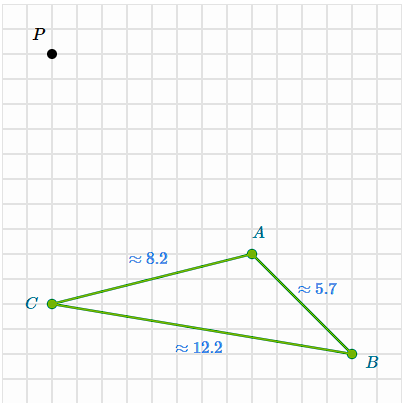
Find the length of the line segments under a scale of 2 with P as the center of dilation
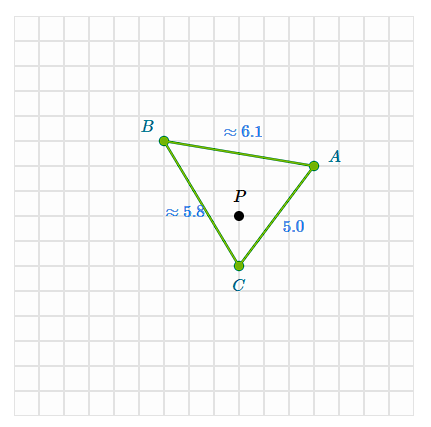
AB ≈ 12.2
BC ≈ 11.7
CA = 10
300
Find the length of the line segments under a scale of 1/2 with P as the center of dilation
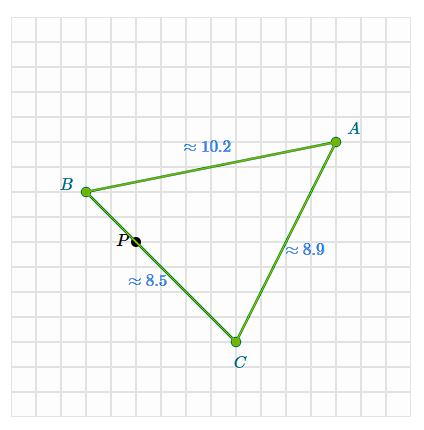
AB ≈ 5.1
BC ≈ 4.2
CA ≈ 4.5
400
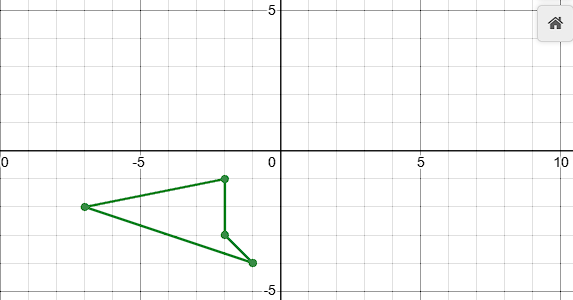
Translate the shape ABCD from (x, y) to (x -7, y +1)
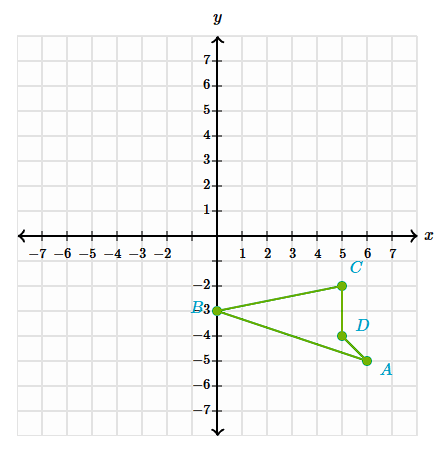
A2:(-1, -4)
B2:(-7, -2)
C2:(-2, -1)
D2:(-2, -3)
400
Rotate the shape PIN by -270 degrees around the origin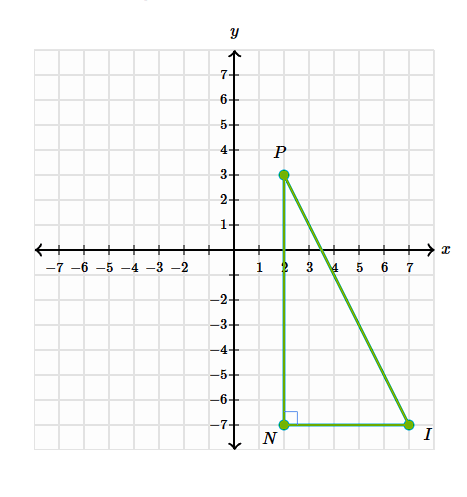
P':(-3, 2)
I':(7, 7)
N':(7, 2)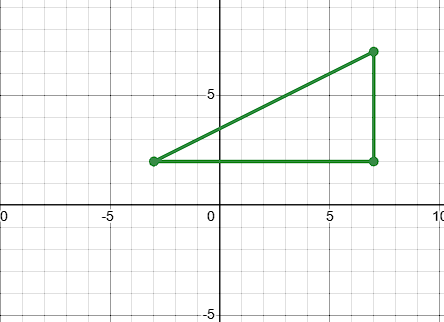
400
Reflect across the x-axis and the y-axis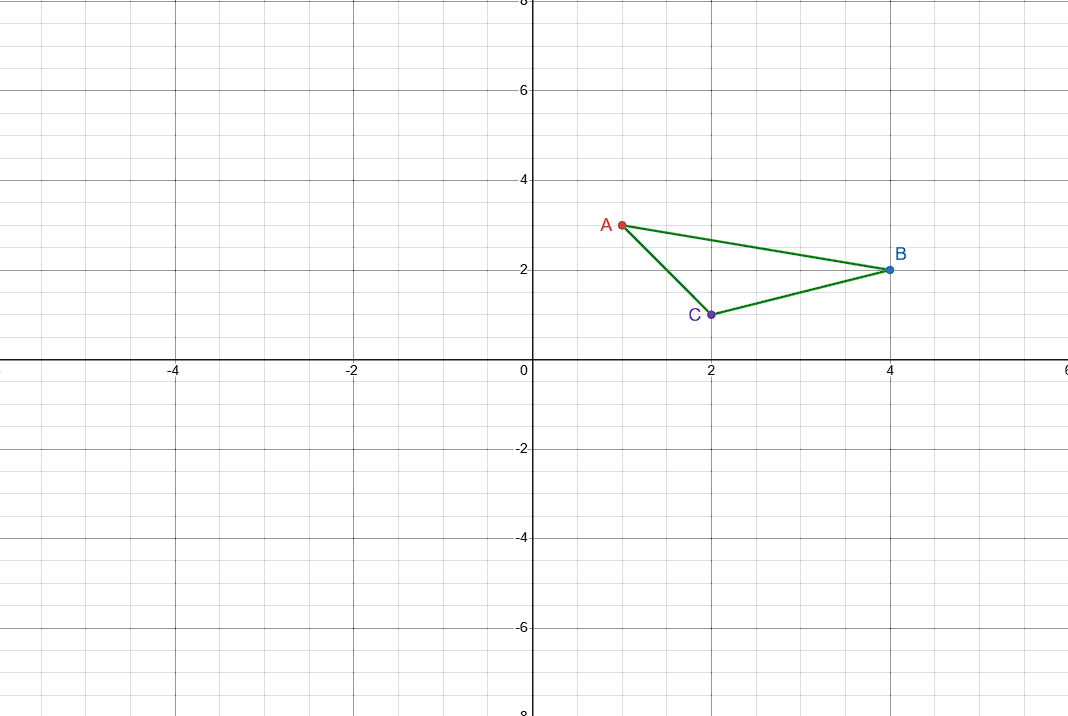
A':(-1, -3)
B':(-4, -2)
C':(-2, -1)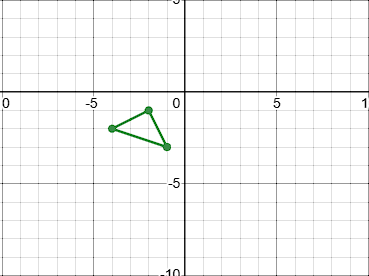
400
Find the length of the line segments under a scale of 1/2 with A as the center of dilation
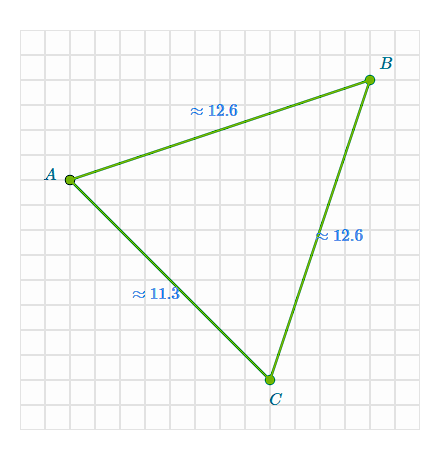
AB ≈ 3.2
BC ≈ 3.2
CA ≈ 2.8
400
Rotate the shape ELM -90 degrees around the origin
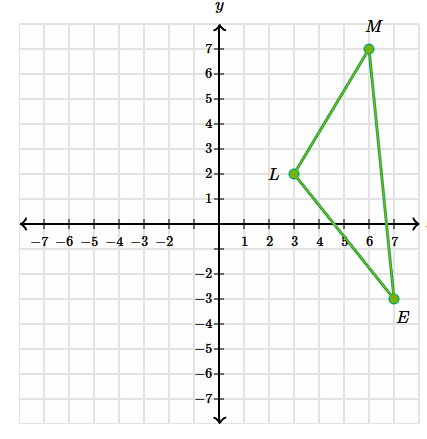
E':(-3, -7)
L':(2, -3)
M':(7, -6)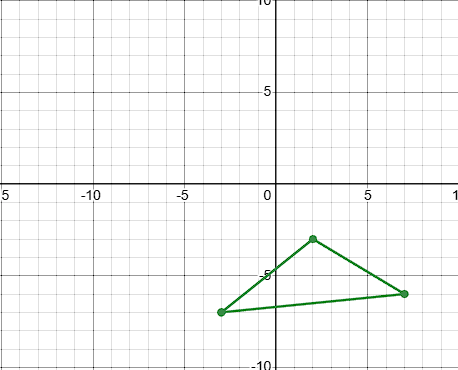
500
Determine the translation between the points
A = (1, 0) A2 = (6, 0)
B = (1, -2) B2 = (6, 4)
C = (5, -5) C2 = (10, 10)
x +5 and y⋅2
500
Rotate the shape JKLM -270 degrees around the origin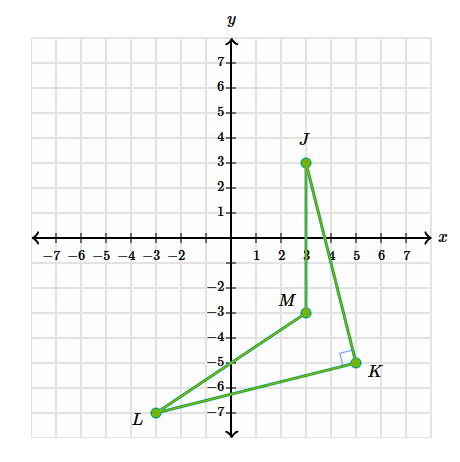
J':(-3, 3)
K':(5, 5)
L':(7, -3)
M':(3, 3)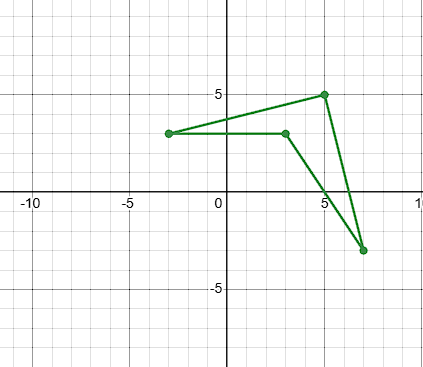
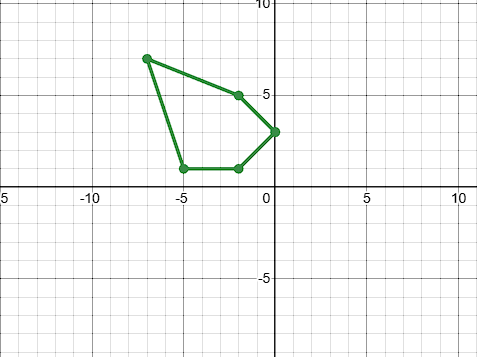
500
Reflect the shape ABCDE along the Y-axis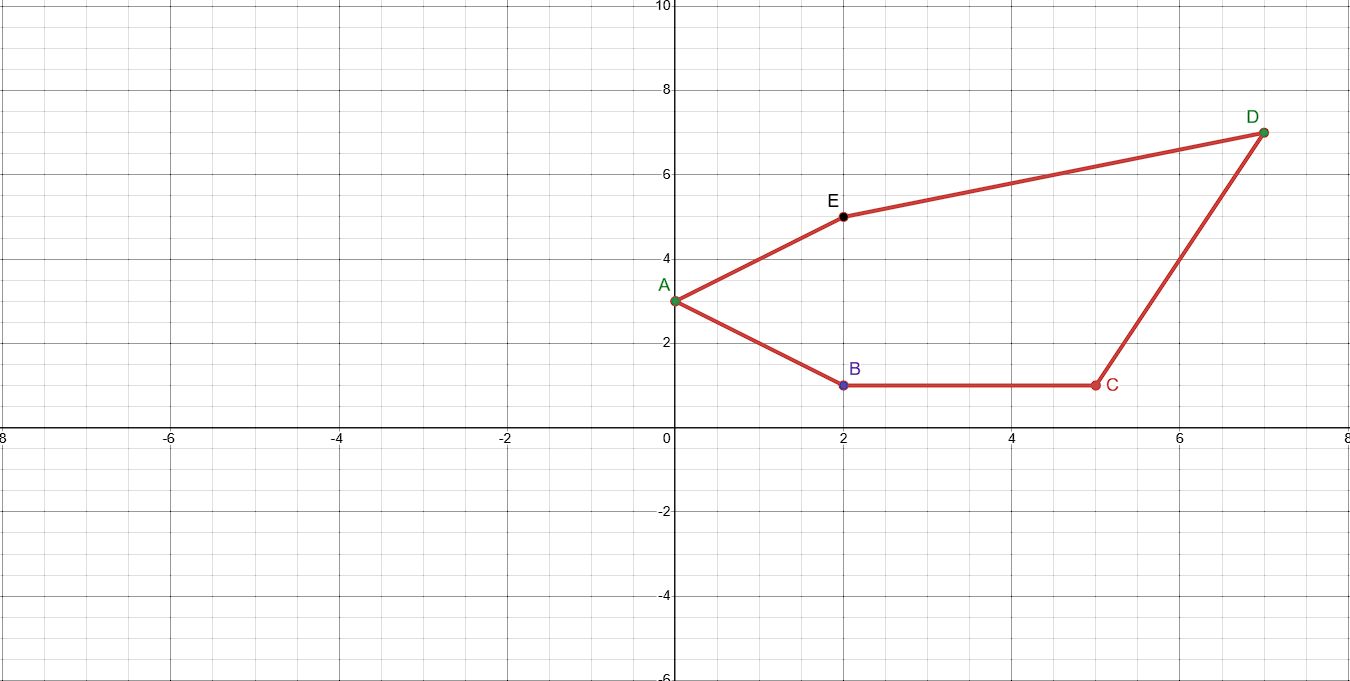
A':(0, 3)
B':(-2, 1)
C':(-5, 1)
D':(-7, 7)
E':(-2, 5)
500
Find the length of the line segments under a scale of 1/3 with P as the center of dilation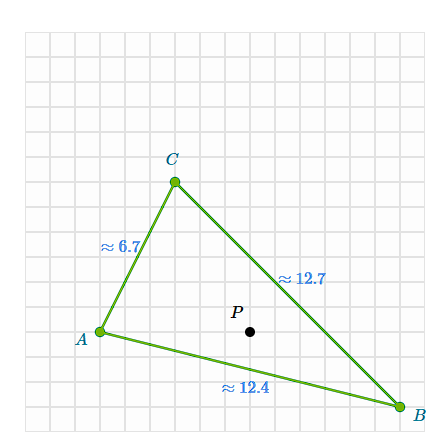
AB ≈ 4.1
BC ≈ 4.2
CA ≈ 2.2
500
Rotate the shape PONY 180 degrees from the origin
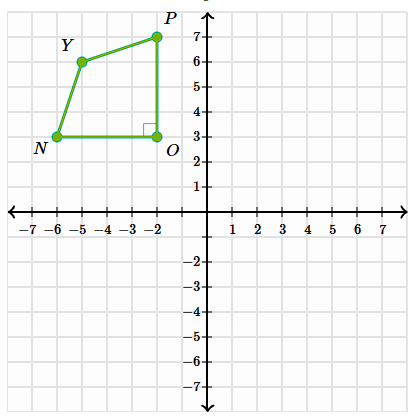
P':(2, -7)
O':(2, -3)
N':(6, -3)
Y':(5, -6)