Math lines
Define
Angles
Billl of Rights
History
300
Describe Complementary angles
Complementary
Complementary angles are two angles whose measures have a sum of 90°. Each angle is the complement of the other.
Complementary angles can be adjacent or non-adjacent.
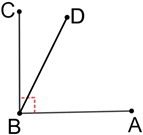Adjacent complementary angles
Non-adjacent complementary angles
For a right triangle, the two non-right or oblique angles must be complementary.
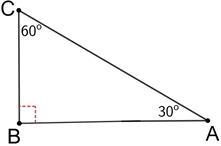
In right triangle ABC above, ∠B = 90° and ∠A + ∠C = 90° so, the nonadjacent angles A and C are complements of each other.
You can determine the complement of a given angle by subtracting it from 90°. For example, the complement of 28° is 62° since 90° - 28° = 62°.
Example:
Look at the diagrams below and see if you can identify the complementary angles.
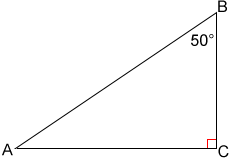
In right triangle ABC above, ∠C = 90° so angles A and B are complementary and, ∠A + 50° = 90°, then ∠A = 40°.
Since two angles do not need to be adjacent to be complementary, given enough information, we do not even need to have a diagram of complementary angles to figure them out.
Example:
Let ∠α and ∠θ be 2 angles that have the variable x in common. If ∠α and ∠θ are complementary where ∠α = (2x - 8)° and ∠θ = (x + 14)°, then
(2x - 8)° + (x + 14)° = 90°3x + 6° = 90°x = 28°
So, ∠α = (2×28 - 8)° = 48° and ∠θ = (28 + 14)° = 42°. Note that 48° + 42° = 90° verifies that ∠α and ∠θ are complementary.
In the study of Trigonometry, the sine value of an angle is equal to the cosine value of its complement. Also, the tangent value of an angle is equal to the cotangent value of its complement. So,
sin(θ) = cos(90°-θ) and sin(90°-θ) = cos(θ)tan(θ) = cot(90°-θ) and tan(90°-θ) = cot(θ)where the complement for θ is 90°-θ
300
An acute angle is....what?
Angles can be classified according to their measure. An acute angle is an angle that measures greater than 0° but less than 90° (the measure of a right angle).
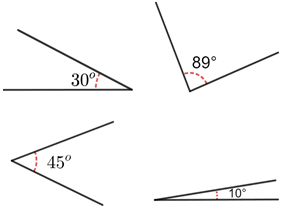Examples of acute angles
300
Describe what is a straight angle is
Straight angle
A straight angle is an angle that has a measure of 180 degrees. It is also equal to the measure of a straight line or two right angles.
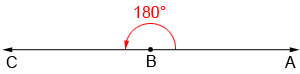
In the figure above, ∠ABC is a straight angle. Rays BA and BC, which form the sides of ∠ABC, lie in opposite directions. Together, rays BA and BC form a line AC.
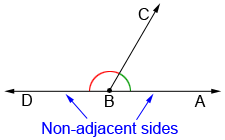
Linear pairs and straight angles
A linear pair is a pair of adjacent angles whose non-adjacent sides form a straight angle.
In the diagram below, ∠ABD and ∠CBD form a linear pair. ∠ABD + ∠CBD = ∠ABC = 180°.
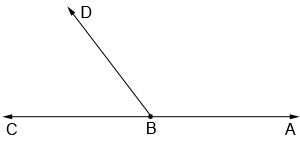
Linear pairs aren't the only type of angles that can form a straight angle. A straight angle can be formed as long as the sum of the angles is 180°:
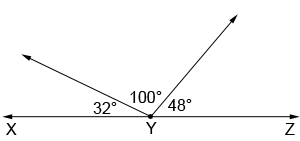
The three angles above share a common vertex, Y, and have a sum of 32° + 100° + 48° = 180°.Thus, ∠XYZ is a straight angle.
300
What is the 6th Amendment of the Bill of Rights?
Amendment VI (6): Rights to a fair trial
In all criminal prosecutions, the accused shall enjoy the right to a speedy and public trial, by an impartial jury of the State and district wherein the crime shall have been committed; which district shall have been previously ascertained by law, and to be informed of the nature and cause of the accusation; to be confronted with the witnesses against him; to have compulsory process for obtaining witnesses in his favor, and to have the assistance of counsel for his defence.
300
In 1888 The Youth's Companion magizine had asked children to collect pennies to purchase flags. How many flags were bought with those pennies?
30,000 flags were purchased.
350
Describe what is an "Alternate exterior angles"
Alternate exterior angles
When a transversal intersects two lines, it forms two pairs of alternate exterior angles. The alternate exterior angles are the opposing pair of exterior angles formed by the transversal and the two lines.
In the diagram below, transversal l intersects lines m and n. ∠1 and ∠4 is one pair of alternate exterior angles, and the other pair is ∠2 and ∠3.
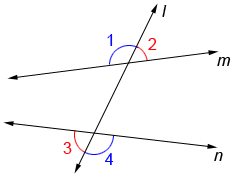
If two lines in a plane are cut by a transversal so that any pair of alternate exterior angles is congruent, the lines are parallel. Conversely, if two lines are parallel, any pair of alternate exterior angles is congruent.
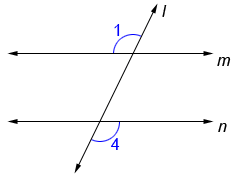
Lines m and n above are cut by transversal l where ∠1≅∠4 so, m//n (// is the symbol for parallel).
Example:
Find the measures of angles 1, 2, and 4 below given that lines m and n are parallel.
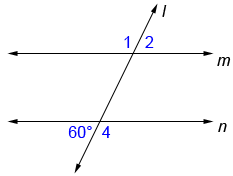
Since lines m and n are parallel, ∠2=60°. Since ∠1 and ∠2 form a straight angle, ∠1=180°-60°=120°. Similarly, since the angle measuring 60° adjacent to ∠4 form a straight angle, ∠4=120°.
350
Describe what is an Adjacent angle
Adjacent
The term "adjacent" is often used to describe angles. It is also used to describe the sides of polygons.
Adjacent angles
Adjacent angles are two angles in a plane that have a common vertex and a common side. They do not have any common interior points. In other words, they do not share any "inside space."
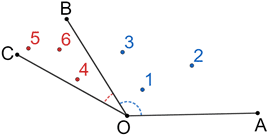
∠COB and ∠AOB are adjacent angles since they have a common vertex, share a common side, and share no common interior points.
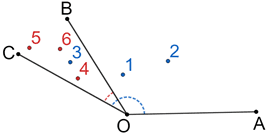
∠COB and ∠AOC are non-adjacent angles. Although they have a common vertex and share a common side, they also share some common interior points, so they cannot be adjacent angles.
∠COD and ∠AOB are non-adjacent angles. Although they share a common vertex and do not share any common interior points, they do not share a common side, so they cannot be adjacent angles. ∠COD and ∠AOB are referred to vertical angles.
∠CAO and ∠BOA are non-adjacent angles. They share a common side and do not share common interior points, but they do not share a common vertex, so they cannot be adjacent angles.
350
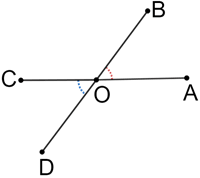
What is a 'linear pair?
Linear pair
A linear pair is a pair of adjacent angles whose non-adjacent sides form a line.
In the diagram above, ∠ABC and ∠DBC form a linear pair. The angles are adjacent, sharing ray BC, and the non-adjacent rays, BA and BD, lie on line AD.
Since the non-adjacent sides of a linear pair form a line, a linear pair of angles is always supplementary. However, just because two angles are supplementary does not mean they form a linear pair. In the diagram below, ∠ABC and ∠DBE are supplementary since 30°+150°=180°, but they do not form a linear pair since they are not adjacent.
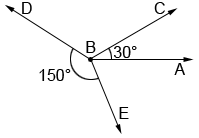
Linear pairs in polygons
Linear pairs are often used in the study of the exterior angles of polygons:
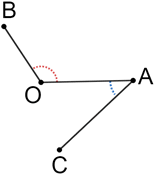
In a triangle, an exterior angle is the sum of its two remote interior angles.
Example:
For △ABC above, ∠A+∠C+∠ABC=180°. Also, ∠ABC and ∠DBC form a linear pair so,
∠ABC + ∠DBC = 180°
Substituting the second equation into the first equation we get,
∠ABC + ∠DBC = ∠A + ∠C + ∠ABC
Subtracting we have,
∠DBC = ∠A + ∠C
where ∠DBC is an exterior angle of ∠ABC and, ∠A and ∠C are the remote interior angles.
The sum of the exterior angles of any polygon is 360°. This can be shown by using linear pairs. The sum of the interior angles of an n-side polygon is 180(n-2)°. There are n angles in the polygon, so there are n linear pairs. Thus, the sum of the exterior angles is:
180n° - 180(n-2)° = 360°
For regular polygon, all of the angles of a are equal. Therefore, all the exterior angles are equal, and can be found by dividing 360° by the number of angles 
.
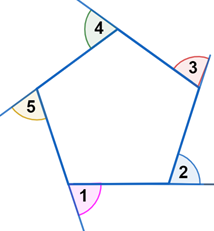
In the regular pentagon above, n = 5. Therefore, the exterior angles measure = 
= 72° each.
350
What is the 7th Amendment of the Bill of Rights?
Amendment VII (7): Rights in civil cases
In Suits at common law, where the value in controversy shall exceed twenty dollars, the right of trial by jury shall be preserved, and no fact tried by a jury shall be otherwise re-examined in any Court of the United States, than according to the rules of the common law
350
What special event was coming up in 1892 where The Youth's Companion wanted flags for every school ?
To celebrate Christopher Columbus for discovering America back in 1492. 400 years earlier.
400
Describe what is an "Alternate interior angle"
Alternate interior angles
When a transversal intersects two lines, it forms two pairs of alternate interior angles. The alternate interior angles are the opposing pair of interior angles formed by the transversal and the two lines.
In the diagram below, transversal l intersects lines m and n. ∠1 and ∠4 are a pair of alternate interior angles and ∠2 and ∠3 are another pair.
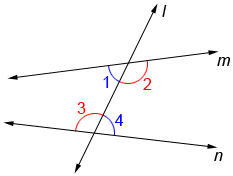
If two lines in a plane are cut by a transversal so that any pair of alternate interior angles is congruent, the lines are parallel. Conversely, if two lines are parallel, any pair of alternate interior angles is congruent.
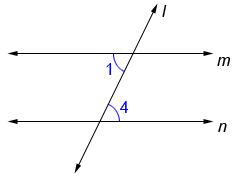
Lines m and n above are cut by transversal l where ∠1≅∠4 so, m//n (// is the symbol for parallel).
Example:
Find the measures of angles 1, 3, and 4 below.
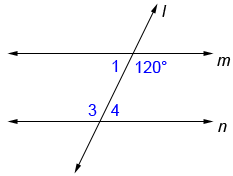
Since lines m and n are parallel, ∠3=120°. Since ∠1 and 120° form a straight angle, ∠1=180°-120°=60°. Similarly, ∠3 and ∠4 form a straight angle so, ∠4=60°.
Alternate interior angles can be used to show similarity for two triangles.
Example:
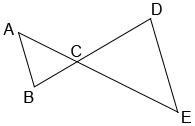
Parallel line segments AB and DE are cut by transversals AE and BD which intersect at point C. Since alternate interior angles are congruent, we can show that △ABC is similar to △EDC.
∠A≅∠E, ∠B≅∠Dcongruent alternate interior angles∠ACB≅∠ECDvertical angles are congruent△ABC~△EDCAA similarity postulate
Note: It is not necessary to prove triangles are similar by showing three pairs of congruent angles. Showing two pairs of congruent angles is sufficient.
400
Describe what an Obtuse angle is
Obtuse
Angles can be classified according to their measure. An obtuse angle is an angle that measures more than a right angle but less than a straight angle. So, an obtuse angle has a measure between 90° and 180°.
Examples of obtuse angles
Angles can also be classified as acute, right, and straight, depending on the measure.
When identifying or measuring an obtuse angle, be careful about the rotation from one side of the angle to the other that produces the angle.
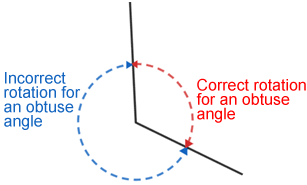
Example:
In the figure below, ∠MON and ∠PON are adjacent angles that are also supplementary. Find the measures of ∠MON and ∠PON and state which angle is an obtuse angle.
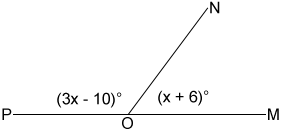
Since ∠MON and ∠PON are supplementary, ∠MON + ∠PON = 180°. If we plug in the expressions for the angle measures, we get,
(3x - 10) + (x + 6) = 1804x - 4 = 180x = 46
So, ∠MON = 46 + 6 = 52°, and ∠PON = 3×46 - 10 = 128°.
∠PON is obtuse since its measure is between 90° and 180°.
Obtuse triangle
The term obtuse is also used in the context of triangles. Whenever a triangle is classified as obtuse, one of its interior angles has a measure between 90° and 180°.
Triangle ABC above is classified as an obtuse triangle since angle A is between 90° and 180°.
It is not possible for a triangle to have more than one obtuse angle. The sum of the measures of the angles in any triangle is 180°, so if one of the angles in the triangle is an obtuse angle, the sum of the other 2 angles must be less than 90° making the other 2 angles acute.
400
Describe a Vertical angle
Vertical angles
Vertical angles are a pair of non-adjacent angles formed when two lines or line segments intersect.
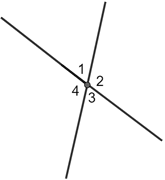
In the diagram above, ∠1 and ∠3 are a pair of vertical angles. ∠2 and ∠4 are also a pair of vertical angles. Vertical angles are congruent, therefore ∠1≅∠3 and ∠2≅∠4.
The term "vertical": in this context does not refer to its more well-known meaning referencing an upright position. You can think of vertical angles as a pair of angles oriented in such a way that reflecting one angle across its vertex will line it up with the other angle. Depending on the orientation of the vertical angles, it can look like the letter "X"
Vertical angles are congruent
One way to show vertical angles are congruent is to use pairs of adjacent angles. In the diagram above, since angles 1 and 2 are adjacent and form a straight angle, ∠1 + ∠2 =180°. Also, since angles 2 and 3 are adjacent and form a linear pair then,
∠1 + ∠2 = 180° = ∠2 + ∠3∠1 = ∠3
So, ∠1≅∠3. Similarly, it can be shown that ∠2≅∠4.
Intersecting chord theorem of angles
When two chords of a circle intersect inside the circle, two pairs of vertical angles are formed. The measure of the angle formed is half the sum of the arcs subtended by the vertical angles formed by the chords of the circle:
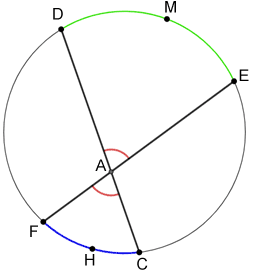
Referencing the diagram above,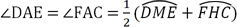 
. This is true for any vertical angles formed by two chords inside the circle. The chords do not have to intersect at the center of the circle for this theorem to be true.
400
What is the 8th Amendment of the Bill of Rights?
Amendment VIII (8): Bails, fines, and punishments
Excessive bail shall not be required, nor excessive fines imposed, nor cruel and unusual punishments inflicted.
400
Francis Bellanty, from The Youth's Companion magazine, went to the U.S. President, Benjamin Harrison, to talk to him about.....what?
......making Columbus Day a holiday.
450
In math terms describe what is a a degree
Degree
A degree is a unit of measure, denoted by the symbol °, used to indicate the measure an angle in a plane. An angle measuring 1°, read 1 degree, is equal to 
of one complete revolution of the angle about its vertex. You can see from the diagram below that the counterclockwise rotation of the terminal side of an angle forms a circular path for the angle.
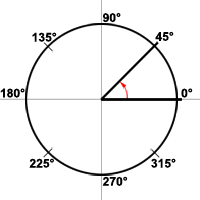
One full rotation is equivalent to 360°. One-quarter of a turn produces an angle that measures 90°, and one-half of a rotation creates an angle of 180°. While angles can have measures greater than what is shown, by doing multiple rotations, we will mostly only look at angle measures up to 360° in the study of Geometry.
Did you know?
Angles can have other units of measure too. Angles can be measured in radians, which compares the arc length produced by the rotation of an angle with the radius of the circle. An angle that measures 180° has a measure of π radians. Another unit of measure for an angle is called the slope. It may also be called grade, incline, gradient, mainfall, pitch or rise. The slope of an angle measures the ratio of the vertical distance over the horizontal distance at the terminal end of the angle. Slope is often represented as a percentage. You may have experience with this unit of measure from climbing or driving up a mountain. The steepness of a hill or mountain is often described in terms of slope, or grade. For example, a hill may have a 5% grade.
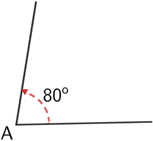
When using the degree symbol be careful not to use it for the name of an angle, only its measure.
The name of the angle shown below is ∠A not ∠A°. When stating its measure, use m∠A = 80° or simply ∠A = 80° where ∠ is the symbol used to denote an angle.
Special angles
Some angles are used more often in Geometry due to their measures:
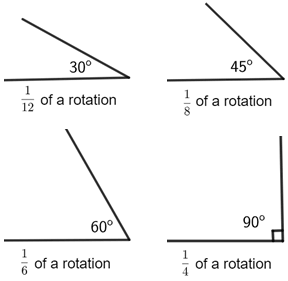
Notice the 90° angle has a small square at its vertex. This notation indicates an angle that measures 90° and it is not necessary to state the angle's measure numerically.
Measuring angles
A protractor is a common tool used to measure angles. Most protractors measure angles in degrees.
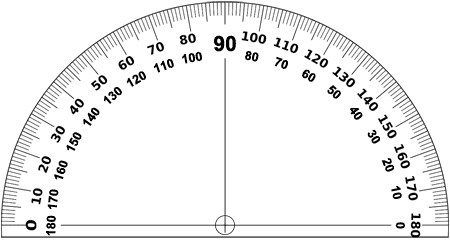
Protractors usually have two sets of numbers. Both sets can be used to measure an angle in degrees. The outside set goes from 0 to 180 degrees where the 0 is on the left side of the protractor. The inner set goes from 180 to 0 degrees where 0 is on the right side of the protractor. Whichever side you line up with the zero-degree line determines which set of numbers to use. See how to measure an angle in degrees using a protractor here.
Did you know?
450
Describe what an Oblique angle is
Oblique angle
An oblique angle is an angle that is not a right angle or any multiple of a right angle. This means that the sides forming the angle cannot be perpendicular.
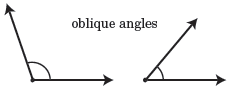
In geometry, acute angles measure between 0 and 90 degrees, and obtuse angles measure between 90 and 180 degrees. Both acute angles and obtuse angles are oblique angles.
The term oblique can also be used to describe plane figures and space figures.
Oblique plane figures
An oblique triangle is a triangle that is not a right triangle.
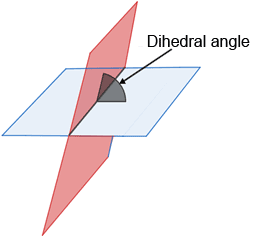
When the intersection of two planes forms an oblique angle, the planes are called oblique planes.
Oblique space figures
The rectangular prism shown below is oblique since its bases are not directly in line with each other.
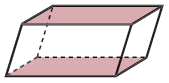
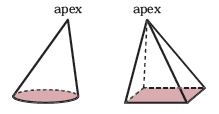
Both the cone and the pyramid shown are also oblique since their apexes are not directly in line with the center of their bases.
450
Describe what an Angle bisector is
Angle bisector
An angle bisector is a line segment, ray, or line that divides an angle into two congruent adjacent angles.
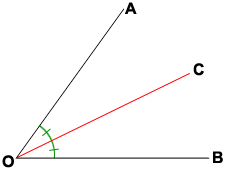
Line segment OC bisects angle AOB above. So, ∠AOC = ∠BOC which means ∠AOC and ∠BOC are congruent angles.
Example:
In the diagram below, TV bisects ∠UTS. Given that ∠STV=60°, we can find ∠UTS.
Since TV bisects ∠UTS, ∠UTV = ∠STV and ∠UTS = ∠UTV + ∠STV, so ∠UTS = 60° + 60° = 120°.
Bisecting an angle with compass and ruler
In geometry, it is possible to bisect an angle using only a compass and ruler. To do so, use the following steps:
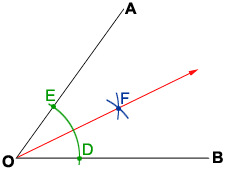
- Place the point of the compass on vertex, O, and draw an arc of a circle such that the arc intersects both sides of the angle at points D and E, as shown in the above figure.
- Draw two separate arcs of equal radius using both points D and E as centers. Make sure the radius is long enough so the arcs of the two circles can intersect at point F.
- Use a ruler to draw a straight ray from O to F. OF bisects the angle AOB.
Things to know about an angle bisector
If a point lies anywhere on an angle bisector, it is equidistant from the 2 sides of the bisected angle; this will be referred to as the equidistance theorem of angle bisectors, or equidistance theorem, for short.
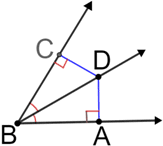
In the figure above, point D lies on bisector BD of angle ABC. The distance from point D to the 2 sides forming angle ABC are equal. So, DC and DA have equal measures.
Conversely, if a point on a line or ray that divides an angle is equidistant from the sides of the angle, the line or ray must be an angle bisector for the angle.
Based on the equidistance theorem, it can be seen that when the two sides that make up an angle are tangent to a circle, the line segment or ray formed by the angle's vertex and the circle's center is the angle's bisector.
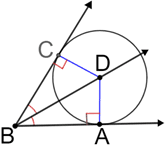
In the diagram above, the two sides of the angle are tangent to the circle and, DC and DA are the distances from the center of the circle to the sides. DC and DA are also the radii of the circle. Since all radii of a circle have equal measure, line BD bisects the angle.
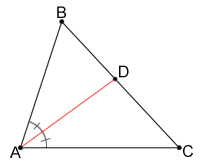
Angle bisector theorem
For a triangle, like the one in the diagram below, if the bisector of angle A intersects side BC at point D, the ratio of the lengths of AB to AC equals the ratio of the length BD to DC. This can be written as: 
.
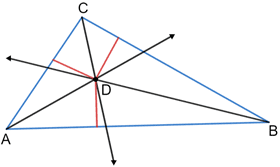
The point at which the three interior angle bisectors intersect is known as the incenter of the triangle. Referencing the diagram below, the three bisecting rays intersect at point D. Point D is the incenter of the triangle and is a point that is equidistant from the three sides of the triangle.
450
What is the 9th Amendment of the Bill of Rights?
Amendment IX (9): Rights retained by the people
The enumeration in the Constitution of certain rights shall not be construed to deny or disparage others retained by the people.
450
1923 The Pledge Alllegiance was changed to
I Pledge Allegiance to the flag of United States of America.....
What were the original words to that line?
I Pledge Allegiance to my flag.....
500
Describe what is a goniometer
Goniometer
A goniometer is an instrument for angle measurement or drawing. It has a moving arm that can be rotated to a precise angular position.
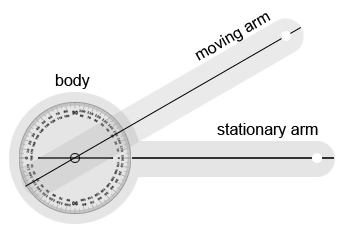
The body the goniometer shown above has two protractors placed on it. The moving arm is attached to the center of the body by a fulcrum and rotates freely counterclockwise or clockwise around it.
You can think of the arms and center of the base of a goniometer as the components of an angle.
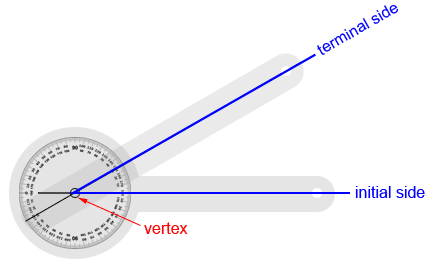
Follow these steps to measure an angle with a goniometer,
- Place the center point of the base over the angle's vertex.
- Place the stationary arm so its center line is over one side (the initial side) of the angle.
- Rotate the movable arm so its center line is over the other side (the terminal side) of the angle.
- The angle measure is the degree number on the protractor that the center line of the movable arm intersects.
500
Describe what a Right angle is
Right angle
A right angle is an angle that measures 90 degrees.
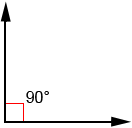
In geometry, a square is typically drawn at the vertex of an angle to indicate it is a right angle.
Lines and planes
If the intersection of two lines forms a right angle, the lines are said to be perpendicular.
If a plane contains a line that intersects another plane at a right angle, it is perpendicular to that plane. Any plane containing a line meeting another plane at a right angle is also perpendicular to that plane. We say that planes and lines that meet each other at right angles are orthogonal.
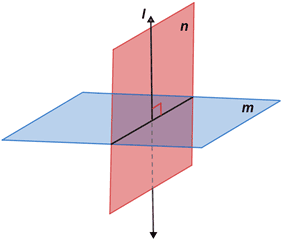Line l in plane n intersects plane m at a right angle so planes n and m are perpendicular planes.
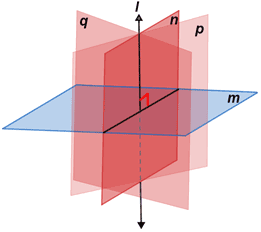Planes n, p, and q contain line l, which meets plane m at a right angle, so planes n, p, and q are also perpendicular to plane m.
Right angles in geometry
Right angles are used widely in geometry. The following are some geometric objects or situations that involve the use of right angles.
A square and rectangle contain four right angles.
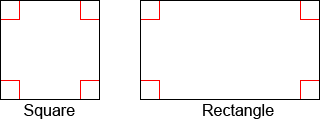
A right triangle contains one right angle
The Cartesian Coordinate System is also known as the rectangular coordinate system because of the right angles formed by the axes and grid lines.
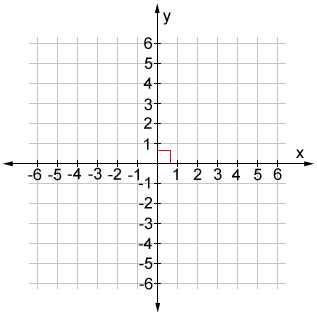
The Cartesian Coordinate System above is a two-dimensional plane where the x-axis and y-axis meet at a right angle at what is called the origin. Also, each horizontal line in the grid intersects each vertical line in the grid at a right angle.
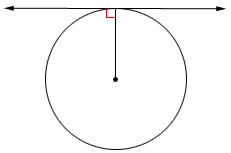
A line tangent to a circle forms a right angle with the circle's radius, containing the point of tangency.
500
Describe what is a Congruent angle
Congruent angles
Congruent angles are angles that have the same measure.
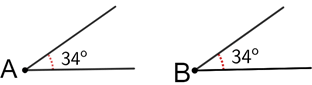
The measure of angles A and B above are both 34° so angles A and B are congruent or ∠A≅∠B, where the symbol ≅ means congruent.
The sides of the angles do not need to have the same length or open in the same direction to be congruent, they only need to have equal measures.
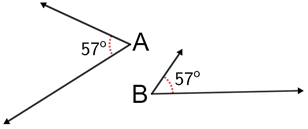
The measure of angles A and B above are 57° so, ∠A=∠B, and ∠A≅∠B,.
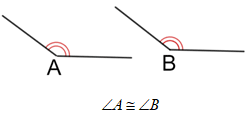
Congruent angles can also be denoted without using specific angle measures by an equal number of arcs placed around the vertices of two angles, as shown below.
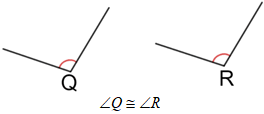
Uses of congruent angles
Whenever an angle is bisected, two congruent angles are formed.
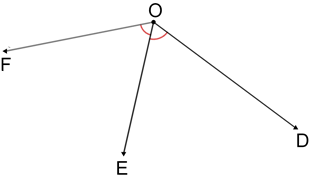
In the figure above, ∠DOF is bisected by OE so, ∠EOF≅∠EOD.
Whenever two lines intersect at a point the vertical angles formed are congruent.
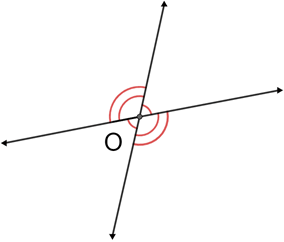
The two lines above intersect at point O so, there are two pairs of vertical angles that are congruent.
Two polygons are said to be similar when their corresponding angles are congruent. The corresponding sides of similar shapes are not necessarily congruent. This means that all congruent shapes are similar, but not all similar shapes are congruent.
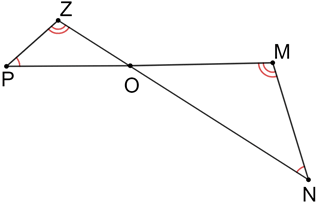
In the figure above, PN and ZN intersect at point O. If ∠P≅∠N and ∠Z≅∠M, then triangle POZ is similar to triangle NOM since the vertical angles at point O forms the 3rd pair of congruent angles for both triangles.
Two polygons are congruent when their corresponding angles and corresponding sides are congruent.
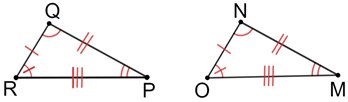
In the figure above, △PQR≅△MNO since ∠P≅∠M, ∠Q≅∠N, and ∠R≅∠O. Additionally, the three sides of △PQR are equal to the three corresponding sides of △MNO. Therefore △PQR and △MNO are congruent.
Whenever a quadrilateral's opposite angles are congruent, the quadrilateral forms a parallelogram.
In quadrilateral ABCD above, ∠A≅∠C, ∠B≅∠D so, the quadrilateral is a parallelogram.
500
What is the 4th Amendment of the Bill of Rights?
Amendment IV (4): Search and arrest warrants
The right of the people to be secure in their persons, houses, papers, and effects, against unreasonable searches and seizures, shall not be violated, and no Warrants shall issue, but upon probable cause, supported by Oath or affirmation, and particularly describing the place to be searched, and the persons or things to be seized.
500
In 1954 two more words were added to the Pledge Allegiance. President Lincon had stated these two words in the Gettsburg Address. What are the two words added?
UNDER GOD.
"one nation, under God" it now reads. This was the last time the Pledge was ever changed.