Trigonometric Identities
Vectors
Law of Sines and Cosines
Polar Equations & Graphs
Miscellaneous
100
Use the sum and difference formulas to determine the exact values of trigonometric expressions and verify identities.
1. cos((2pi)/3+(7pi)/4)
2. sin(((3pi)/2)-((5pi)/3))
3. Show csc(pi/2-x)=sec(x)
1. (sqrt(6)-sqrt(2))/4
2. -1/2
3. 1/(sin(pi/2-x))=1/(sin(pi/2)cosx-cos(pi/2)sinx)=1/cosx
100
Determine the component form of a vector.
a=⟨2,4⟩,b=⟨−1,6⟩
⟨1,10⟩
100
Use Heron's Formula to determine the area of an oblique triangle.
a=4m, b=7m, c=9m
6sqrt(5)m^2
100
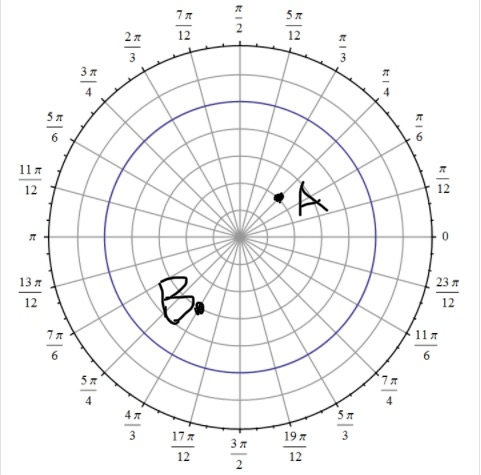
Graph polar coordinates on a polar plane.)
A. (2,pi/3)
B. (3,-2pi/3)
100
Use trigonometric identities (addition, subtraction, double-angle) to rewrite expressions within trigonometric equations and solve, determining all possible solutions and/or solutions on a given interval.
Determine the solutions in the interval [0,2π) for 2sin(2x)-1=0
pi/12, (5pi)/12,(13pi)/12,(17pi)/12
200
Use the double-angle, half-angle, and product-to-sum/sum-to-product formulas to determine the exact values of trigonometric expressions and verify identities.
1. tan(2(30°))
2. cos(15°)
3. .5(cos(75)+cos(-15))
4. Show (sec(x)+1)/(sec(x)-1)=cot^2(x/2)
1. sqrt(3)
2. (sqrt(6)+sqrt(2))/4
3. sqrt(6)/4
4. cot^2(x/2)=1/(tan^2(x/2))=((1+cosx)/sinx)^2=(1+cosx)^2/sin^2x=(1+cosx)^2/(1-cos^2x)=((1+cosx)(1+cosx))/((1-cosx)(1+cosx))=(1+cosx)/(1-cosx)
200
Determine the magnitude and direction of a vector.
Initial point 𝑃 (−8,1)
Terminal point 𝑄(−2,−5)
Magnitude = 6sqrt(2)
Direction = -45°
200
Use two sides and the included angle to determine the area of an oblique triangle.
a=42m, b=58m, angle C=34°
681.1m
200
Determine multiple representations of the following coordinate on the polar plane including those with positive and negative values of r.
(1,(3pi)/2)
(1,-pi/2)
(-1,pi/2)
(1,(7pi)/2)
(-1,(5pi)/2)
200
Use trigonometric identities (half-angle and sum-to-product) to rewrite expressions within trigonometric equations and solve, determining all possible solutions and/or solutions on a given interval.
Determine the solutions in the interval [0,2π) for 4sin2(x)-3=0
pi/3,(2pi)/3
300
Determine relevant trigonometric identities and formulas and use them to simplify expressions.
1. cos2(10x)-sin2(10x)
2. (1-cos(6x))/(1+cos(6x))
1. cos(20x)
2. tan2(3x)
300
Express a vector in terms of the unit vectors i and j.
|v|=42, θ=45°
21sqrt(2)i+21sqrt(2)j
300
Solve application problems involving oblique triangles with special angles, including those involving navigational heading/bearing.
Two ships leave a port at the same time. One ship takes a bearing of N43°E, the other takes a bearing of N17°W. Both ships are traveling at a speed of 32mph. How far apart, to the nearest mile, will the ships be after traveling for 4 hours?
128 miles
300
Convert coordinates and equations from rectangular form to polar form and vice versa.
1. (6,-2) to polar
2. (5,(7pi)/4) to rect.
3. 4x+2y=8 to polar
4. r=-6sin(theta) to rect.
1. (2sqrt(10), tan^(-1)(-1/3))
2.((5sqrt(2))/2,(5sqrt(2))/2)
3. r=8/(4costheta+2sintheta)
4. x^2+y^2+6y=0
300
Solve application problems involving periodic data.
The pendulum of a grandfather clock makes one complete swing every 5 seconds. The maximum angle that the pendulum makes with respect to its rest position is 14°. We know from physical principles that the angle θ between the pendulum and its rest position changes in a simple harmonic fashion. Determine an equation that describes the size of the angle θ as a function of time, t.
theta(t)=14sin((2pi)/5t)
400
Solve trigonometric equations algebraically, determining all possible solutions and/or solutions on a given interval.
Determine the solutions in the interval [0,2π) for 2cos2(x)-1=0
pi/4,(7pi)/4
400
Perform vector addition, subtraction, and scalar multiplication.
Given that u = ⟨4,-4⟩ and v = ⟨−2,8⟩ evaluate the following.
1. u + v =
2. v - u =
3. 3u + v =
1. ⟨2,4⟩
2. ⟨-6,12⟩
3. ⟨10,-4⟩
400
Determine the number of different oblique triangles that exist given certain side lengths and angle measures.
1. angle B=25°, angle C=74°, a=7
2. angle C=34°, c=23, a=24
1. 1 triangle
2. 2 triangles
400
Sketch graphs of polar equations by hand and with a graphing utility.
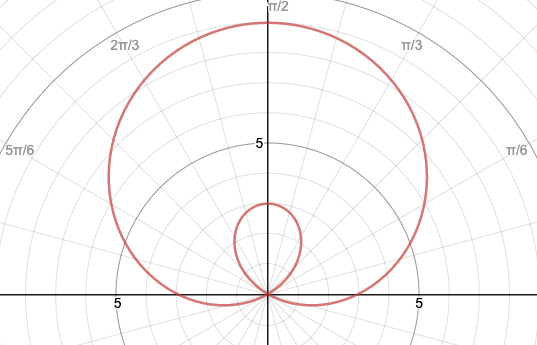
1. r = 3 + 6sinθ
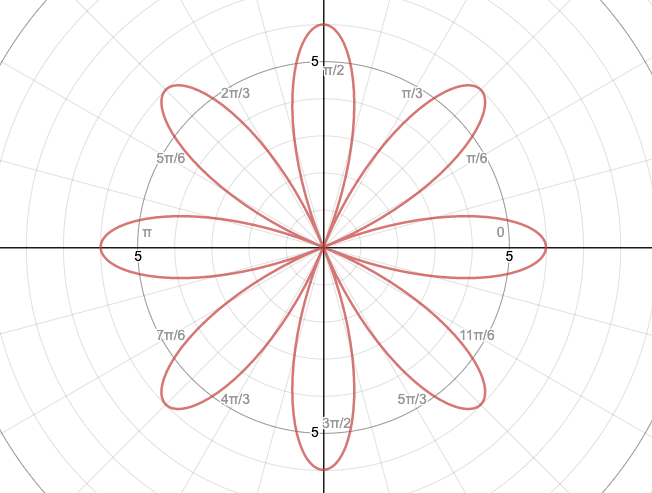
2. r = 6cos(4θ)
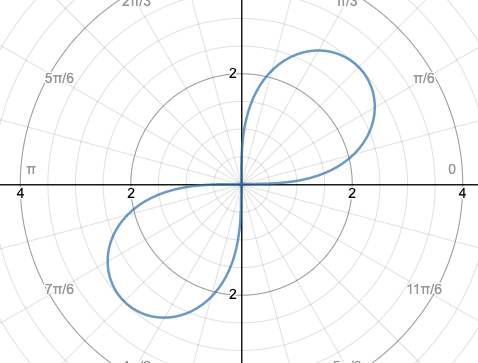
3. r2 = 32sin(2θ)
1.
2. 
3.
400
Write a polar equation of a given polar graph. (Pt. 2)
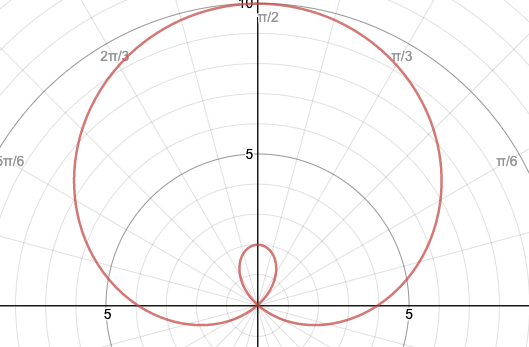
r=4+6sintheta
500
Utilize trigonometric identities and algebraic techniques to solve trigonometric equations, determining all possible solutions and/or solutions on a given interval.
Determine the solutions in the interval [0,2π) given sin2(x)-5sin(x)-6=0
(3pi)/2
500
Solve application problems involving navigational heading/bearing using vectors.
A ship leaves port on a bearing of 32° and travels 6.8 miles. The ship then turns due east and travels 4.7 miles. How far is the ship from the port and what is its bearing?
10.1 miles from port
bearing of 23.24°
500
Use the Law of Sines and the Law of Cosines to solve oblique triangles (determine all missing sides lengths and angle measures).
1. angle B=123°, a=2, b=4
2. angle A=41°, angle B=43°, c=17
1. c=2.54, angle A=24.79°, angle C=32.21°
2. angle C=96°, a=11.21, b=11.66
500
Write a polar equation of a given polar graph.
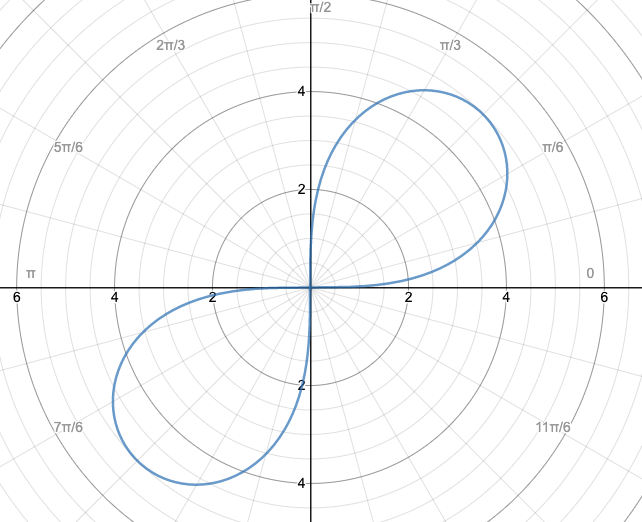
r^2=5^2sin(2theta)
500
Determine the magnitude and direction of a vector. (Pt. 2)
Initial point 𝑃 (2,13)
Terminal point 𝑄(−4,9)
Magnitude
2sqrt(13)
Direction
tan-1(-4/-6) = tan-1(2/3)