Order of Operations
Word Problems
Linear Equations
Business Problems
Solving Equations
100
2 times 3^2-8
10
100
You decide to spend your Friday night at a local concert. The ticket cost $10. A soda at the show costs you $2 each.
Identify your variables and write an equation to represent the situation.
Let x be the number of sodas purchased.
Let y be the total cost of the evening.
y=2x+10
100
Write the formula for slope.
m=\frac{y_2-y_1}{x_2-x_1}
100
What does the break-even point represent?
It is the intersection of the Revenue function and the Cost function.
It indicates where the business sells enough product so they do not lose money and they do not make a profit.
100
8x=4
x=\frac{1}{2}
200
(16-4)\div 6+3
5
200
For babysitting, Nicole charges a flat fee of $12, plus $10 per hour. Write an equation for the money Nicole earns, E, after h hours of babysitting.
What do you think the slope and the y-intercept represent?
E=10h+12
The slope is 10 because 10 is the hourly rate of change.
The y-intercept is 12 because 12 is the base amount charged for babysitting.
200
Suppose you graphed the three following equations.
y=x \quad \quad \quad \quad y=2x \quad \quad \quad \quad y=3x
How are the graphs alike? How are they different? Compare the slopes.
Each of the graphs is a linear line, increasing and going through the origin.
However, y=3x is the steepest line and y=x is the least steep line. The bigger the coefficient of x, the steeper the line.
200
What is the equilibrium point?
It represents the quantity of product to be produced and the price it should be sold at so there is no shortage or surplus of product.
It is the intersection point for the Supply function and the Demand function.
200
21-2x=-9x
x=-3
300
2+4(5-3)-3^2-15
-14
300
A canoe rental service charges a $20 transportation fee and $30 dollars an hour to rent a canoe. Write an equation representing the cost, y, of renting a canoe for x hours.
What is the cost of renting the canoe for 6 hours?
y=30x+20
For 6 hours, it will cost $200.
300
Write an equation for the points below. Use slope-intercept form.
(30,180) \quad \quad \quad \quad (50,220)
y=2x+120
300
Suppose that the demand and price for a youth wristwatch are related by
p=D(q)=16-1.25q
where p is the price in dollars and q is the quantity demanded (in hundreds). Find the price if the demand for the wristwatch is 400 watches.
The price should be $11.
300
5x-6=3x+4
x=5
400
36\div 3 \times 2 -3^3
-3
400
A water tank already contains 55 gallons of water when Baxter begins to fill it. Water flows into the tank at a rate of 8 gallons per minute. Write a linear equation to model this situation.
Find the volume of water in the tank 25 minutes after Baxter begins filling the tank.
y=8x+55
There are 255 gallons of water after 25 minutes.
400
Write an equation for the line below.
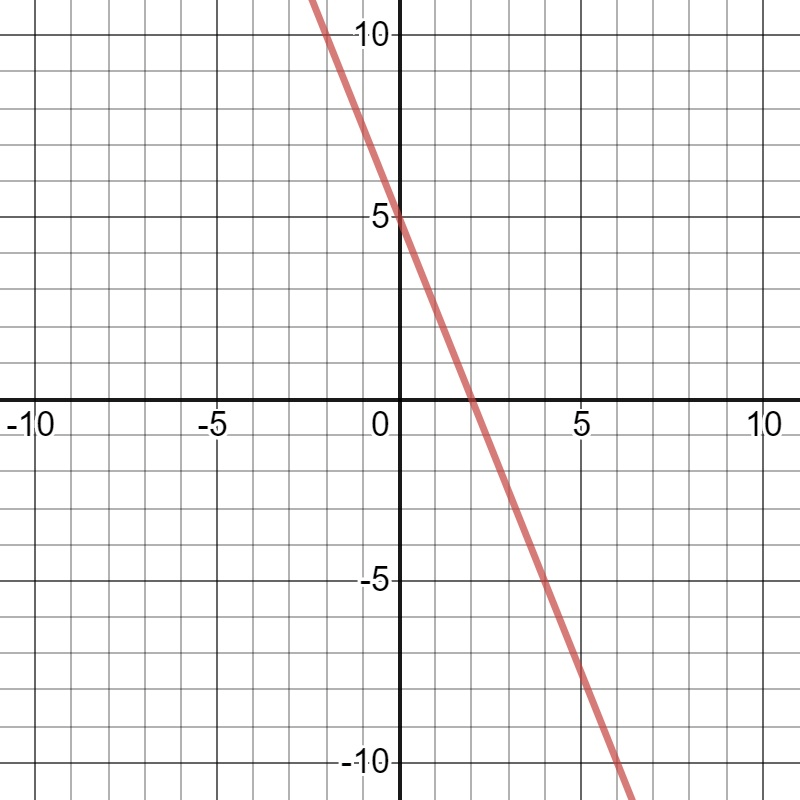
y=-\frac{5}{2}x+5
400
To produce x units of a championship medal cost
C(x)=12x+39
The revenue is
R(x)=25x
Find the profit from 250 units.
The profit is $3211.
400
3(x-3)=6x-21
x=4
500
2[8-2(30 \div 3)-2]+20
-8
500
Casey has a small business making dessert baskets. She estimates that her fixed weekly costs for rent and electricity are $200. The ingredients for one dessert basket cost $2.50.
Her total costs for the week before were $562.50. How many dessert baskets did she make the week before?
y=2.50x+200
Casey made 145 dessert baskets to earn $562.50.
500
A caterer charges $120 to cater a party for 15 people and $200 for 25 people. Assume that the cost, y, is a linear function of the number of x people. Write an equation in slope-intercept form for this function.
y=8x
500
Write a cost function given the following information.
Fixed cost: $100
50 items cost $1600 to produce
C(x)=30x+100
500
Joanne sells silk-screened T-shirts at community festivals and crafts fairs. Her cost function is
C(x)=3.50x+90
Her revenue function is
R(x)=9x
How many T-shirts must she produce and sell in order to break even?
17 shirts