This is the negation of:
"No one buys Swedish Fish."
This is the probability of rolling an even-number or a 3 on a fair, 6-sided die.
4/6 or 2/3 or .67
After finding the Deviations, this is the next step when calculating the Standard Deviation from a List of Data:
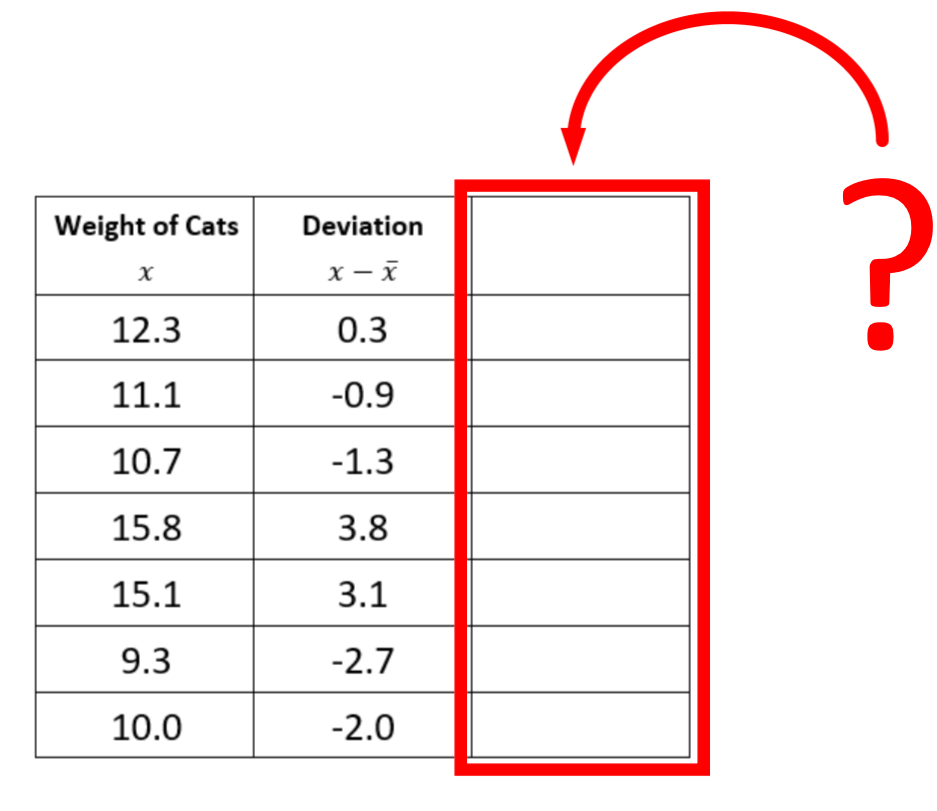
Square the Deviations
Zoe buys a pair of roller-skates for $5,000. She borrows money from Elise who charges her 5% Add-On Interest for 6 years. Zoe wants to know what she'll owe Elise.
This is the formula Zoe uses.
The Add-On Interest Formula
FV=P(1+rt)
This is the negation of:
"I am well-rested and not anxious."
"I am not well-rested or I am anxious."
17,013,360
This is the value of the area beneath the normal curve in the following picture:
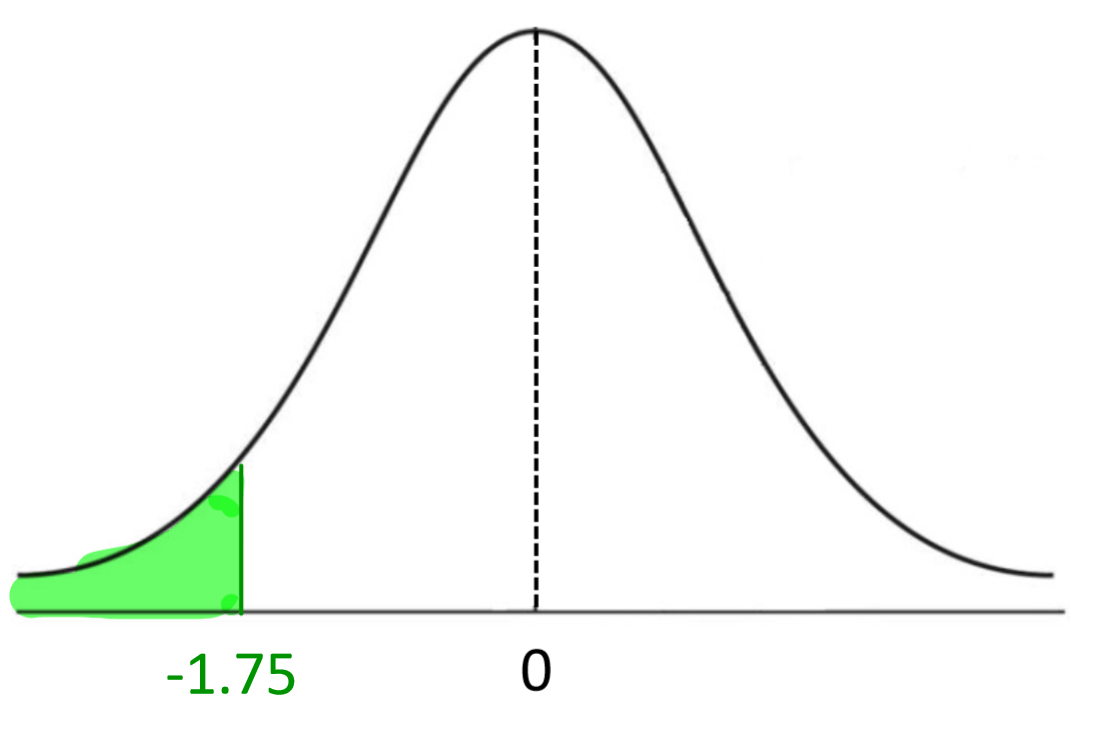
.0401
Calculate the Annual Yield on an account earning 5.5% compounded daily.
Round your answer to two decimal points, like this: 3.25%.
5.65%
This sentence can be represented with the Venn Diagram below:
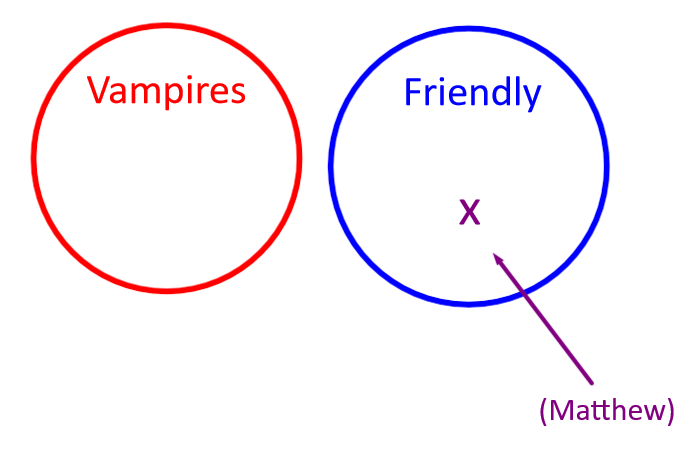
"No vampires are friendly. Matthew is friendly."
100 people chose blue.
101 people chose white.
119 people chose blue or white.
This number goes in the highlighted space:
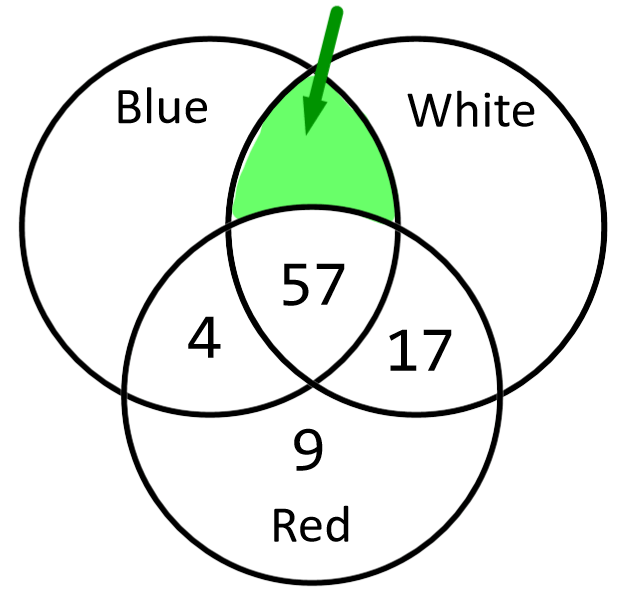
25
This is the Margin of Error derived from the following formula:
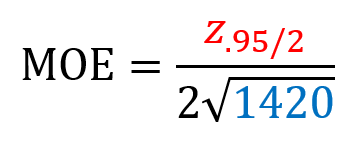
2.6%
10 years ago, Caci bought a house for $1,500,000. She paid 10% down and financed the rest with a 30-year mortgage at 4.56% interest. She wants to know how much money she still owes on the house.
This is the formula Caci uses.
The Unpaid Balance Formula
UB=P(1+i)^n-pymt*[(1+i)^n - 1]/i
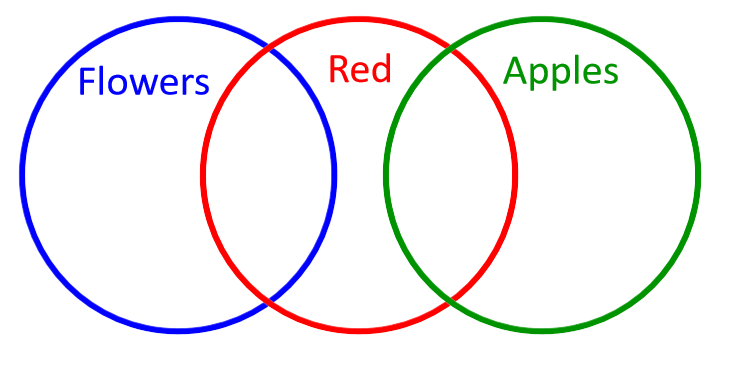
This Venn Diagram invalidates the argument:
"Some Flowers are Red. Some Apples are Red. Therefore, some Apples are Flowers."
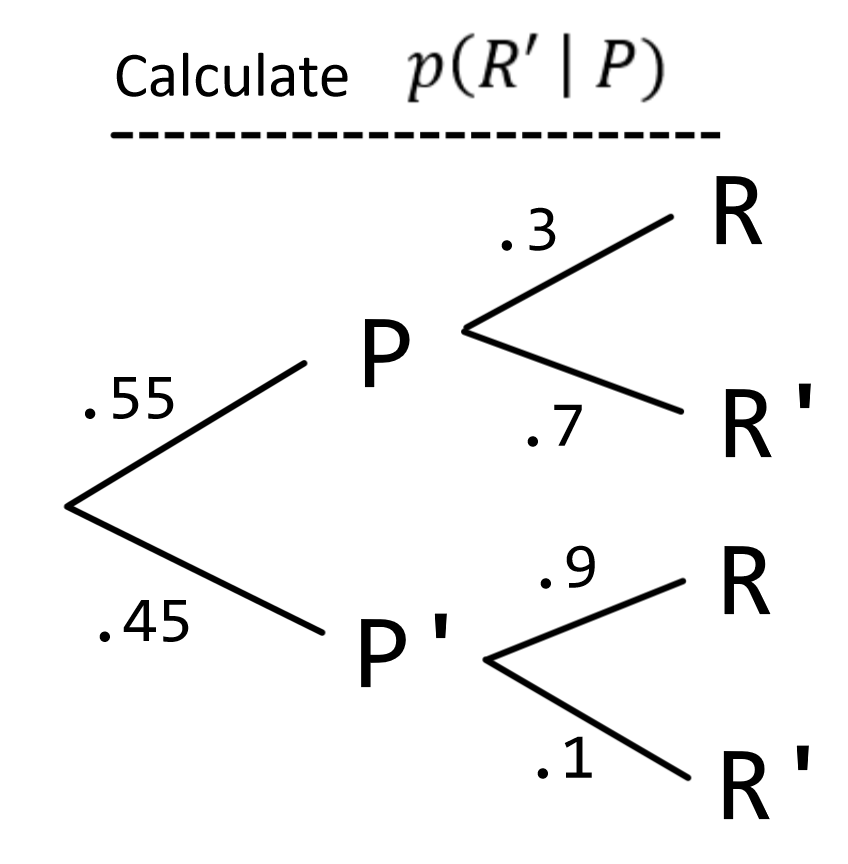
.7
This is the value of the area beneath the normal curve in the following picture:
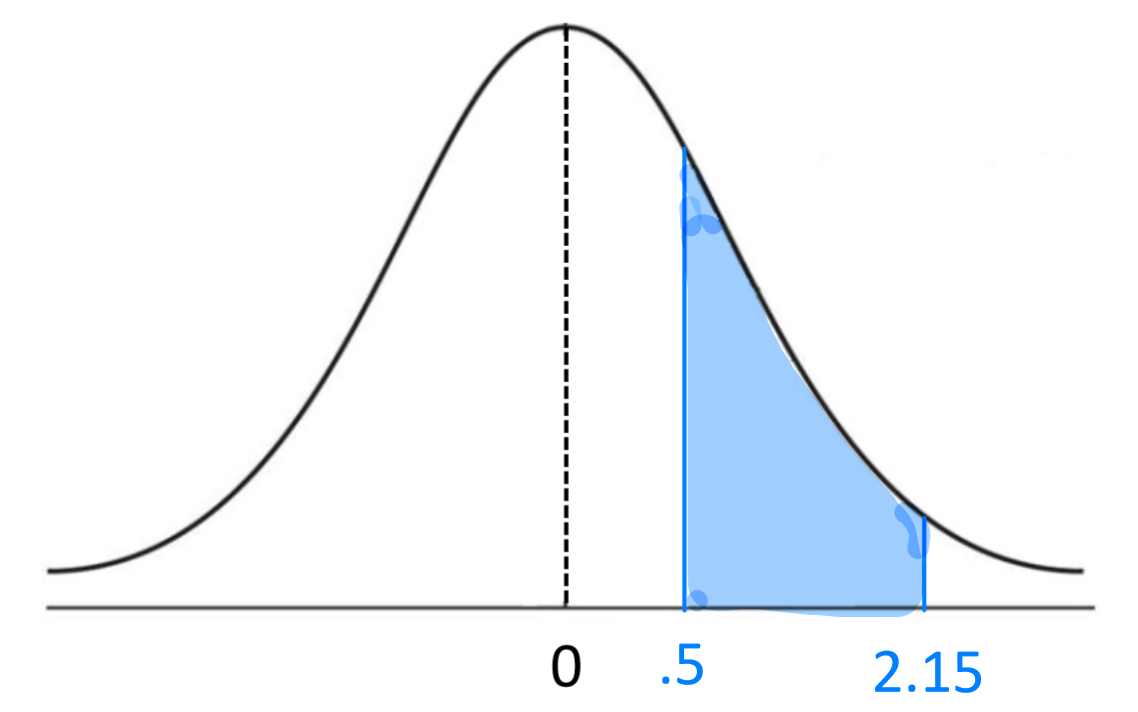
.2927
Use your calculator to evaluate:
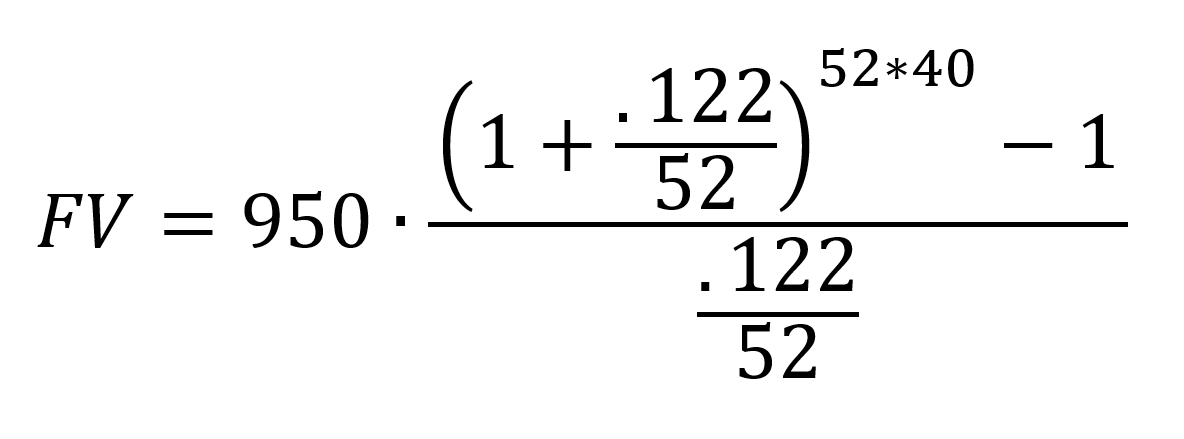
$52,590,936.93
This is the validity of the argument presented in the Truth Table below:
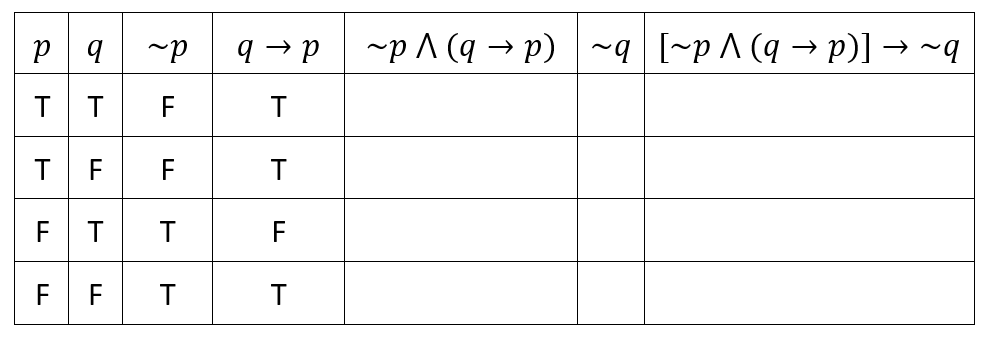
Valid.
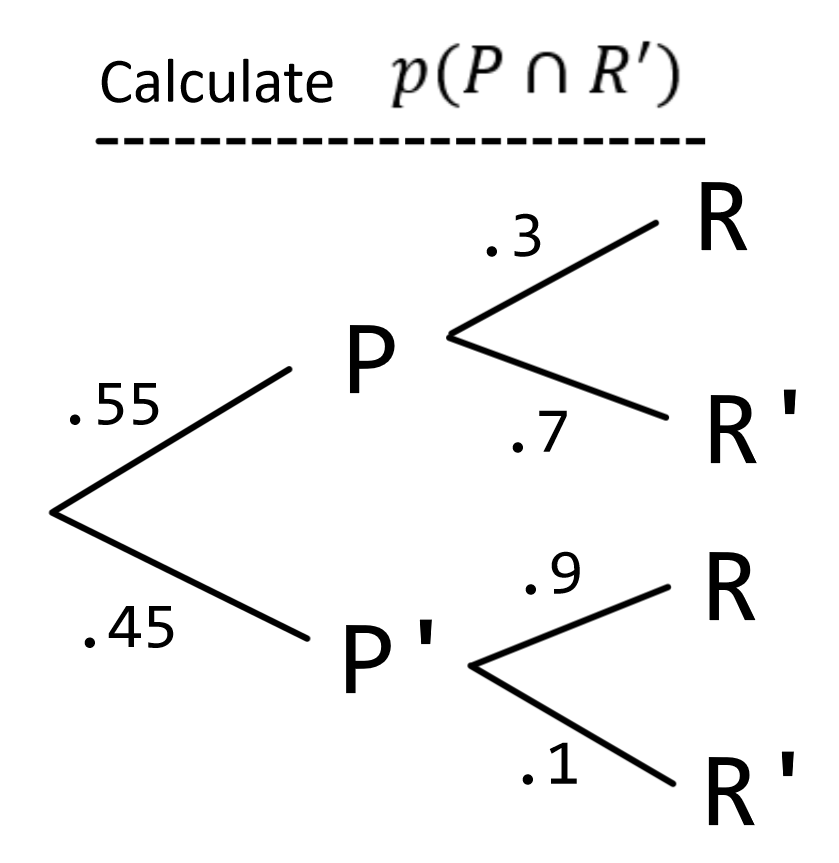
.385
The following set of data has a Mean of 15.4 and a Standard Deviation of 5.0:
11, 12, 23, 12, 15, 10, 19, 21
This is the percent of data that falls within one Standard Deviation of the Mean.
62.5%
The amount of interest earned on $700,000 invested in a 15-year CD earning 9.25% interest compounded bi-weekly.
$2,096,483.53