I'm being totally rational!
Divide and Conquer
Conjugates Come in Pairs!
ZERO to Hero
Everything Parabolas!
100
What's the horizontal asymptote of:
r(x) = \frac{5x^2}{3x^2-10x+2}
y = \frac{5}{3}
100
If 5 is a zero, what is it's corresponding factor?
(x - 5)
100
If a + bi is a zero of a given function, what also has to be a zero?
a - bi
100
What is a "zero" of a function f(x)?
A value of x that makes f(x)=0.
(Also an x-intercept!)
100
What is the vertex and axis of symmetry off(x) = -(x+3)^2 + 4 ?
Vertex = (-3,4)
Axis of Symmetry: x = -3
200
What's the y-intercept of:
r(x)=\frac{x^2+6}{2x^2+7x-3}
(0,-2)
200
If (x + 11) is the divisor, what number would we use to do the dividing in synthetic division?
-11
200
What is the complex conjugate of 7i?
-7i
200
What is the zero of f(x) = 12+x ?
zero = -12
200
Where does f(x) = -(x+3)^2 + 4 have a minimum or maximum, and what is the value?
Maximum value of 4 at x = -3
300
What's the vertical asymptote(s) of:
r(x)=\frac{7}{x^2-64}
x = -8, 8
300
How do we write our final answers after completing polynomial division?
P(x) = D(x) \cdot Q(x) + R(x)
300
What is (x+\sqrt5)(x-\sqrt5) ?
x^2-5
300
Find all the zeros of
f(x) = x^2 + 169
zeros = -13i, 13i
300
Put f(x) = -x^2-6x-5 into standard form.
f(x) = -(x+3)^2 + 4
400
What are the x-intercepts of:
r(x)=\frac{x^2+2x-15}{x^2+17}
(-5,0) and (3,0)
400
Divide P(x) = 3x^2 - 7x + 11 by D(x) = x-3 . Find the quotient and the remainder.
Q(x) = 3x + 2
and
R(x) = 17
( 3x^2-7x+11 = (x-3)(3x+2)+17 )!
400
What is (x + 7i)(x - 7i)?
x^2+49
400
Find the real and imaginary zeros of P(x) = x^4 - 8x^2 - 9
zeros = -i, i, -9, 9
400
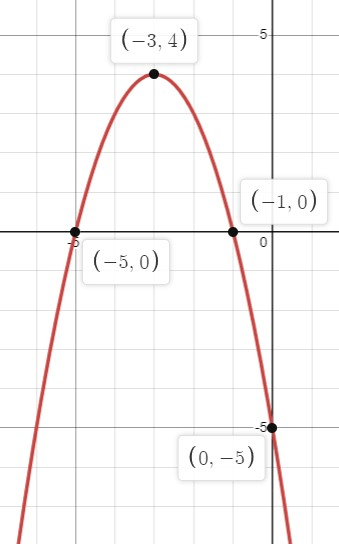
Find the x- and y-intercepts of
f(x)=-x^2-6x-5
x-intercepts: (-5,0) and (-1,0)
y-intercept: (0,-5)
500
Solve \frac{9}{y+3}+\frac{3}{y-3}=\frac{9y-3}{y^2-9}
y=5
500
Divide P(x) = 2x^3 - 13x^2 + 19x + 1 by D(x) = x+8 . Find the quotient and the remainder.
Q(x) = 2x^2+3x-5
and
R(x) = 41
( 2x^3-13x^2+19x+1 = (x+8)(2x^2+2x-5)+41 )!
500
Create a polynomial of degree 4 that has rational coefficients, and has the zeros -7i, and sqrt5
*HINT* Find the conjugates!
x^4+44x^2-245
500
Use the quadratic formula to find the exact solutions of x^2+4x-10=0
x = -2+\sqrt{14}, -2-\sqrt{14}
500
DAILY DOUBLE!
Each team will send one member up to the board to graph the quadratic function: f(x)=-(x+3)^2+4
