Transformations & Parallel Lines
Triangles & Quadrilaterals
More Triangles & Quadrilaterals
Quadratics & Exponents
Radicals & Factoring
100
One endpoint is A(-3,4) and the midpoint is M(4,-6). Find the other endpoint B.
B(11,-16)
100
Find the range of x
3 < x < 17
100
Order the sides from shortest to longest. (Picture is not drawn to scale)
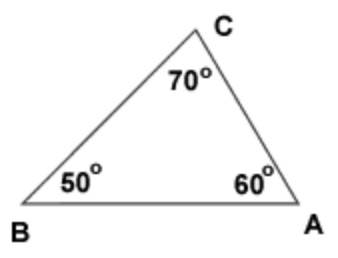
AC, BC, AB
100
Simplify
((5x^4)/y^2)^3
(125x^12)/y^6
100
Factor
10x2 - 25x
5x(2x - 5)
200
Describe the following transformations:
(x, y) -> (x+3, y-1) -> (y,x) -> (3x, 3y)
Translate 3 to the right and 1 down, reflect over y=x, and dilate the x & y by a factor of 3
200
Nine angles of a decagon sum to 1388. Find the 10th angle.
10th Angle = 52
200
Determine whether a triangle can be formed with the given side lengths. (Show your work)
6 inches, 8 inches, 15 inches
No, 6 + 8 "is not greater than" 15
200
Multiply (3x - 8)(2x + 5)
6x2 - x - 40
200
Factor
5x2 - 28x - 12
(5x + 2)(x - 6)
300
Find the distance between A(1/2, -5) and B(-1/4, 7)
(Radical form or round to the nearest hundredth)
(3√257)/4 or 12.02
300
x = 28 and y = 54
300
Solve for y
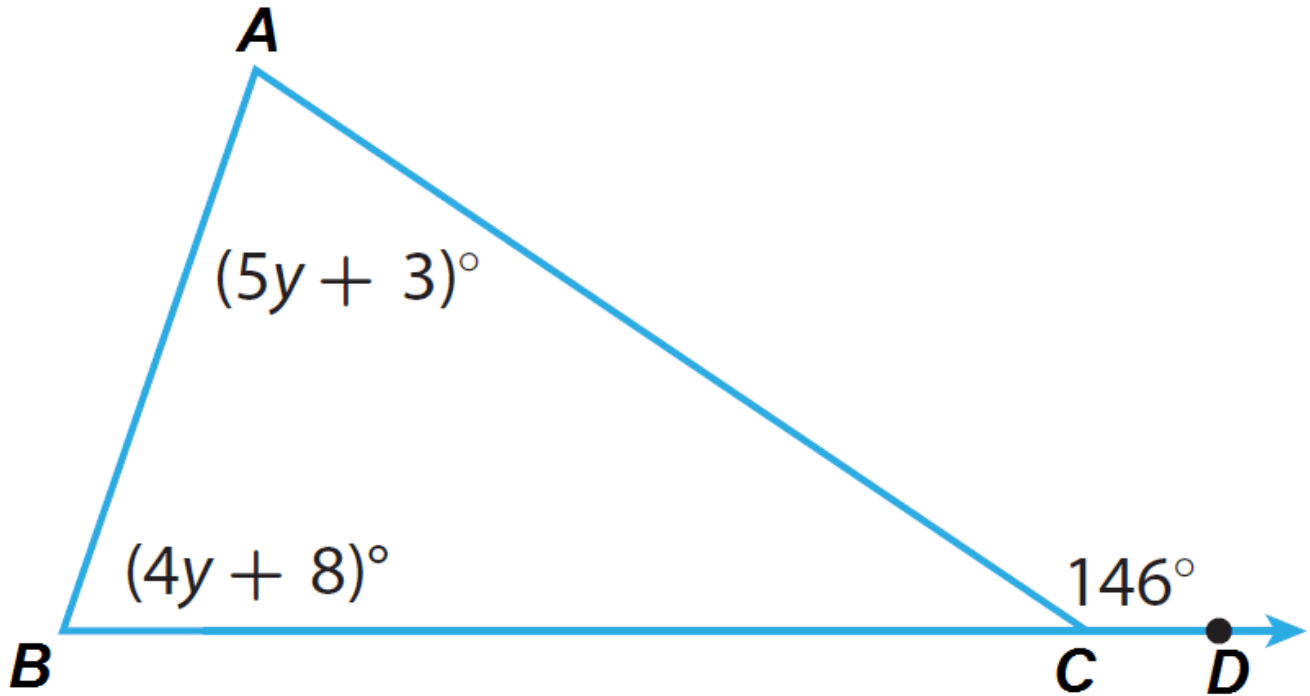
y = 15
300
Solve by factoring x2 +5x - 6 = 0
x = -6 and x = 1
300
Factor
9x2 - 121
(3x - 11)(3x + 11)
400
Triangle ABC has the following points A(4, 8), B(-2, -2), and C(5, -1). The triangle is reflected over the y-axis first, reflected over the y=x second, and finally translated three units up and two to the right. Where is the finally location of point C? (Write your answer as a point.)
C'''(1, -2)
400
x = 24
400
Which postulate or theorem, could you use to prove the triangles congruent?
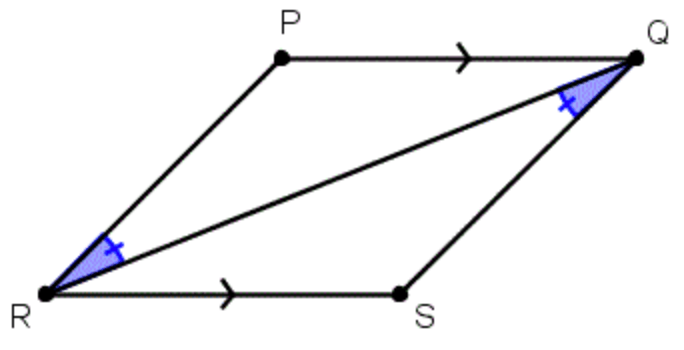
ASA
400
The current population for an island is 120,000 and increases at a rate of 4% per year for x years. Find the number of people on the island after 15 years.
216,113 people
400
Solve
x2 - 40 = 0
x =
+-2sqrt(10)
500
Find the area of the shaded region. Round to the nearest tenth.
21.5 units2
500
Given triangle ABC, m∠A = 50 and m∠B = 2x+22. If m∠C is 20 degrees greater than ∠B , what is the value of x?
x = 16.5
500
Find y
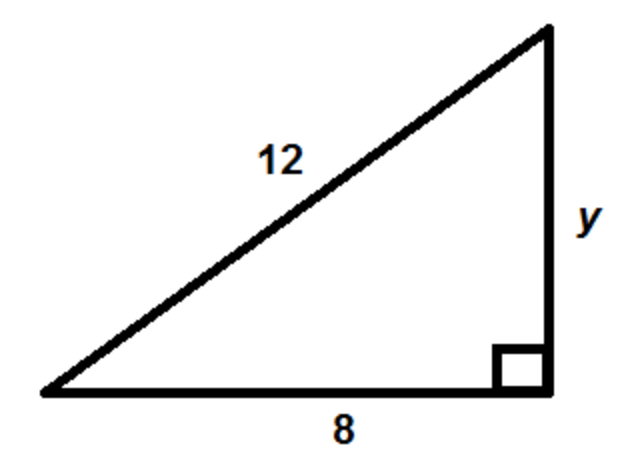
4sqrt(5) or 8.9
500
Find the vertex of 2x2 - 12x + 3
(3, -15)
500
Simplify
5sqrt(3)-sqrt(27)+sqrt(12)
4sqrt(3)
600
Find the midpoint of the following two points: A(4,-6) and B(-3,4)
M(.5,-1)
600
Find ∠BAC and ∠D
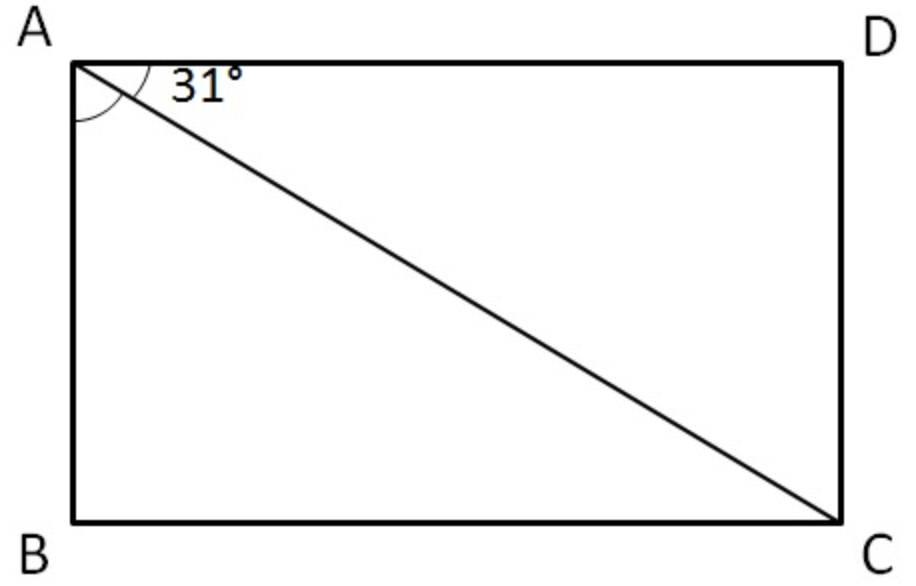
∠BAC = 59, ∠D = 90
600
Find the value of x given that the m∠ABD = 76
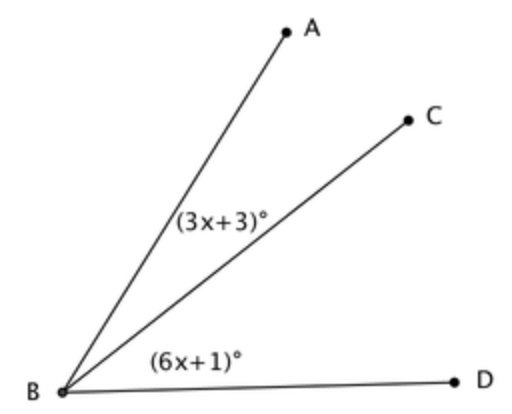
x = 8
600
Identify the y-intercept
y = x2 - 8x + 10
(0,10)
700
Solve for x
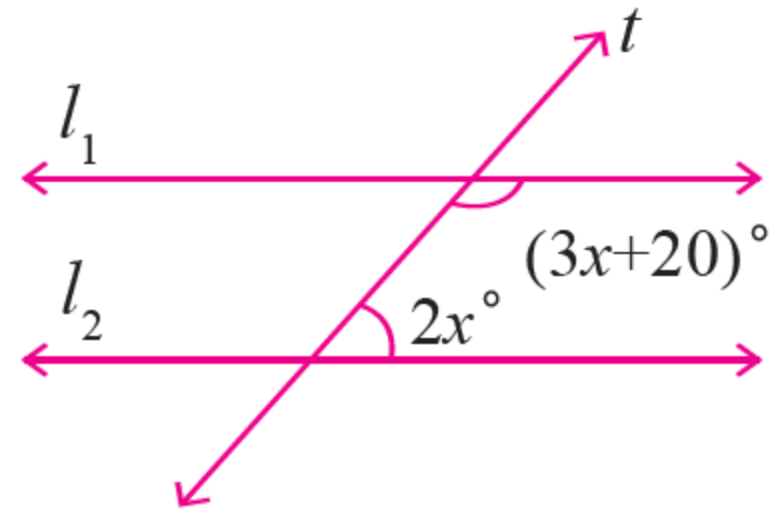
x = 32
700
Multiply
(a - 7)2
a2 - 14a + 49