Rules
Absolute Value Equations
Absolute Value Equations
Absolute Value Inequalities
Characteristics of Graphs
100
What do you do first to solve an Absolute Value Equation?
Isolate the Absolute Value
100
| z - 13 | = 21
What is { -8 , 34 }
100
| d + 5 | = 9
What is { 4 , -14 }
100
| w + 9 | < 17
-26 < w < 8
100
State the zeros
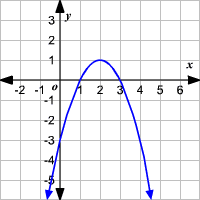
x= 1 and x= 3
200
What is the maximum number of solutions you have when solving absolute value?
Two
200
| d + 1 | = 7
What is { 6 , -8 }
200
| a - 6 | = 10
What is { 16 , -4 }
200
2 | x + 5 | > 22
x< -16 , x>6
200
State the maximum and minimum value
Max: y=1
Min: none
300
Absolute value equations can never be equal to this
A negative number
300
5 | q + 6 | = 20
What is { -2 , -10 }
300
3 |4x - 1| - 5 = 10
What is { -1, 3/2 }
300
3 | 2a - 4 | < 0
No solution
300
State the domain and range
Domain: (-infinity, +infinity)
Range: (-infinity, 1]
400
If the absolute value equation is equal to 0, how many solutions are there?
One
400
| p + 1 | + 10 = 5
What is { No Solution }
400
|2x - 3| = - 1
What is { No Solution }
400
Taylor solved this problem and said that the solutions are b> 13/3, b< 7/3. Taaylor made an error. Find the error and explain why it's wrong.
-5| 3b - 10 | > 15
No Solution because postives are never lessthan negatives.
Taylor kept going even when the absolute value was less than a negative number.
400
State the end behavior.
As x-->+inf, f(x)--> -inf
As x--> -inf, f(x)--> -inf
500
If the absolute value is greater than a negative number, how many solutions are there?
Infinitely Many
All Real Numbers
500
|3x + 2| +5 = 5
What is { -2/3}
500
-6 -|2x+5| = -6
What is { 5/2} ?
500
-5 | 3z + 8 | - 5 > -20
-11/3 < z < -5/3
500
State the increasing and decreasing intervals
Increasing: (-inf, 2]
Decreasing: [2, +inf)