Absolute Extrema
Price Elasticity of Demand
Graphing Characteristics
Random
100
Define "Absolute Extrema"
This is the max/min of a function on an interval and where the function reaches its maximum/minimum possible value.
100
What is Price Elasticity of Demand?
Price elasticity describes what would happen if your current price (p) is raised by 1%. The demand (q) will decrease by E(p) % from the current demand.
This is essentially a measure of how sensitive your demand is to a change in price.
100
Define "critical point"
A critical point is a point where f'(x) is either 0 or undefined.
100
If at the critical point x=2, f'' is positive, is this a maximum or minimum value?
Minimum.
200
Where are the two places you will find a global maximum or minimum?
At critical points and endpoints.
200
If...
E(p) > 1
E(p) < 1
E(p) = 1
Then demand is... (3 answers)
In this order: Elastic, Inelastic, and of unitary elasticity.
200
Define "Inflection Point"
An inflection point is where f''(x) = 0
200
Find the derivative at x = 1.5 and x = 2
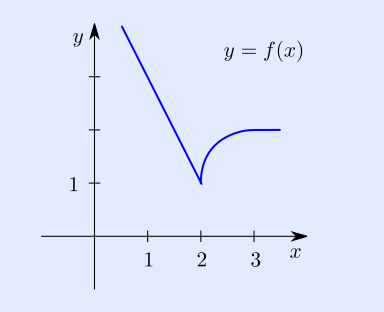
Note: The points (1,3) and (2,1) are on this graph.
The slope of the line is -2 so
f'(1.5) = -2
Notice how at x=2 there is a sharp cusp, this means that
f'(2) -> DNE
300
On this interval [-2,2], is the absolute maximum on the end of the interval or at a critical point? What about the absolute minimum?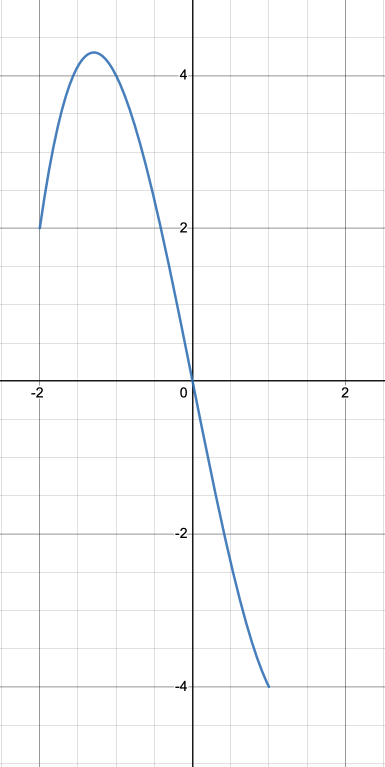
The absolute maximum is at a critical point.
The absolute minimum is at the end of the interval (x=2).
300
How should you change your price if...
- Demand is elastic
- Demand is inelastic
- Demand is of unitary elasticity
Lower, Raise, Leave it!
300
Find the critical value(s) of the following function:
f(x) = x^3+6x^2+12x
x = -2
400
Determine the absolute minimum and maximum of the following function on the interval [0,2]:
f(x)= x^2-x^3
Absolute Min: (2,-4)
Absolute Max:
(2/3,4/27)
400
For the following demand function, state whether demand is elastic, inelastic, or of unitary elasticity at p = 1
q = 5 + p/(p+8)
This is inelastic at E(1) since it will result in a negative number (by inspection). But if you wanted to find the exact value of E(1), you could plug in 1 to E(p), which would give you -0.012, meaning this is BARELY inelastic and your price is almost just right.
400
Estimate where f(x) is concave up given this graph of f'(x)
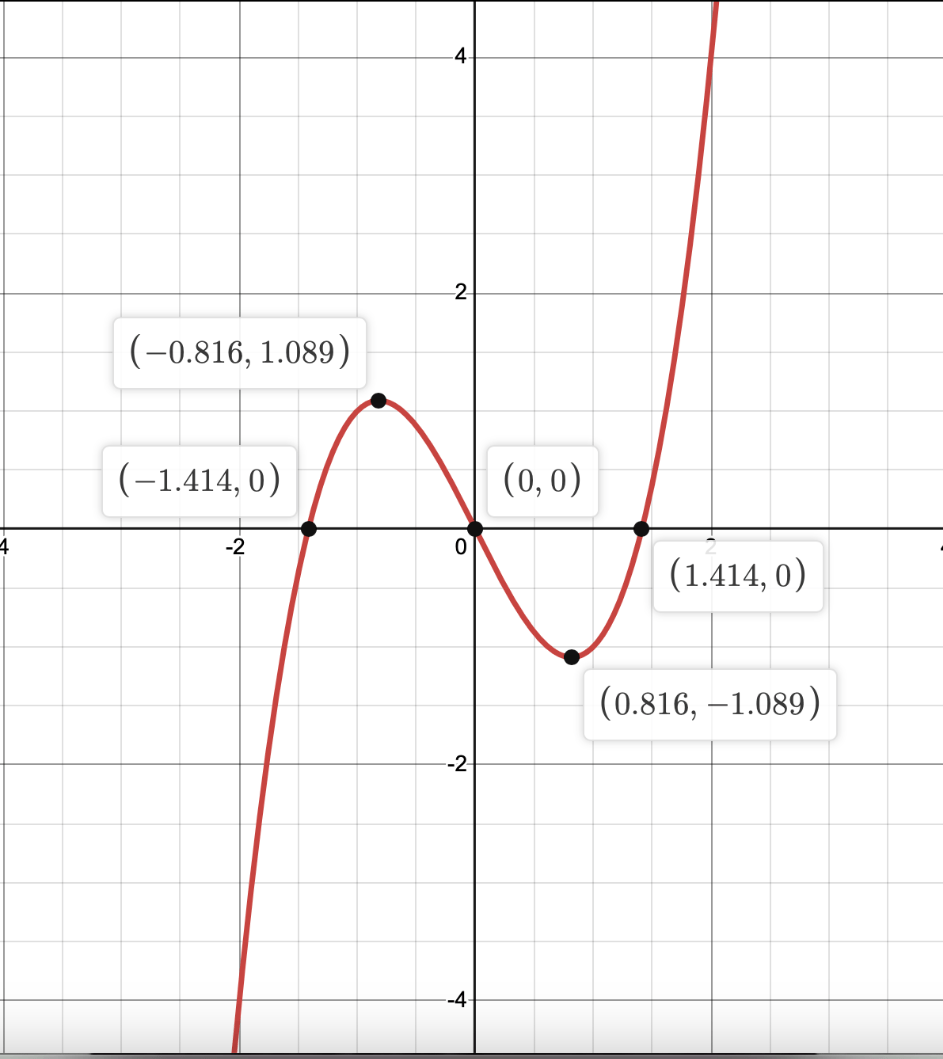
(-infty,-0.816) U(0.816,infty)
400
Find the horizontal and vertical asymptotes of the following function (if they exist):
f(x) = (x^2-2x-3)/(x+2)
VA: x = -2
HA: None
500
If revenue is given by the function R(p)=1700p-10p2, what price would tickets have to be sold at to maximize revenue?
$85
500
Give an example of products that might be elastic or inelastic in their demand. Think about the definition here.
Things like prescription medicines are extremely inelastic - A raise in price doesn't affect demand much because these are a necessity (This is why prescription medicines can be so expensive!)
Infrequently bought items like cars, appliances, etc. are highly elastic. If a car is too expensive, someone might delay buying it, OR go buy your competitor's car. The price very highly affects the demand.
500
If they exist, find the critical values, intervals of increasing/decreasing, inflection values, and interval of concavity for the following function
f(x) = x^2-4x
Critical Value: x=2
Inc: (2,inf) Dec: (-inf, 2)
No inflection values. F''(x) is always positive so f(x) is always concave up (-inf,inf)