Which of the following are quadratics: y=x+2, y=3-x2, y=x3 + x2, and y = 7 + 2x
What is y=3-x2
What are the xintercepts of y=(x+5)(x-3)
(-5,0) and (3,0)
Write in standard form y=-3(x-6)(x+5)
What is y=-3x2 + 3x + 90
Find the vertex of y=3(x-4)2 - 7 and describe the transformations.
What is (4,-7). Transformations are Right 4, Down 7, and Vertical Stretch
How long is the soccer ball in the air and what is the vertex of the ball? (Hint: x-axis is time and y-axis is height)
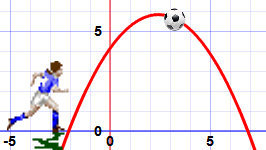
What is 9 seconds and the vertex is approximately (2.5,6)
Find the axis of symmetry, vertex, and determine if the quadratic is a max or min. 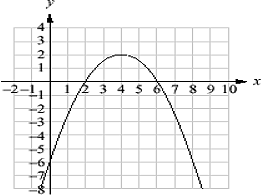
What is AOS: x=4, Vertex: (4,2), and the quadratic is a max
What is the y-intercept of y=(x+7)(x+8)
(0, 56)
Find the axis of symmetry for y = x2 - 8x + 10
What is AOS x=4
Graph y = 2(x+3)2 - 2

The International Space Agency has finally landed a robotic explorer on an extra-solar planet. Some probes are extended from the lander's body to conduct various tests. To demonstrate the crushing weight of gravity on this planet, the lander's camera is aimed at a probe's ground-level ejection port, and the port launches a baseball directly upwards with a path of h(t) = -49t2 +147t. Assuming no winds and that the probe can scurry out of the way in time, how long will it take for the ball to smack back into the surface and find the max height of the ball? Time is in seconds and height is in feet. (Hint: Graph the function)
What is the ball takes 3 seconds to return to the surface and the max height of the ball is 110.25 ft.
Find the domain and range. (Assume the curve continues beyond the graph)

What is Domain: -∞ < x < ∞ or (-∞,∞) or All Real Numbers, Range: y≤2 or (-∞,2]
What are the xintercepts of y = (x+4)(2x-1)
What is (-4,0) and (1/2,0)
Find the axis of symmetry, vertex, and determine if it is a max or min. y = 2x2 + 10x - 3
What is AOS x=-2.5, Vertex (-2.5,-15.5), and the quadratic is a min
The point (3,72) is on the parabola y=ax2. Find the value of a?
What is a=8
The height in feet of a rock thrown upward from a cliff above the ocean beach is given by the function s(t) = -16t2+64t+50, where t is the time in seconds.
Find the maximum height above the beach that the rock will attain
114 feet
Reduce the square root of 264.
2 sqrt 66
Factor and find its' xintercepts: y=x2+4x-5
What is y=(x+5)(x-1)
(-5,0) and (1,0)
What are the EXACT xintercepts of y = x2+5x-7
What is ([-5+sqrt53]/2 , 0) and ([-5-sqrt53]/2 , 0)
Write the following equation in vertex form: y=x2+6x+16
What is y=(x+3)2 + 7
The height in feet of a rock thrown upward from a cliff above the ocean beach is given by the function s(t) = -16t2+64t+50, where t is the time in seconds.
When will the rock hit the beach?
4.669 sec
Find the range of y=x2 - 5 (Hint: Graph the function)
What is Range: y≥-5 or [-5,∞)
What is the AOS and Vertex of a quadratic FUNction with the equation y = (x-3)(x-10)
What is x = 6.5 and (6.5, -12.25)
What is the standard form for a quadratic function that has zeros of (-8,0) and (4,0)?
What is y=x2+4x-32
Given the vertex (2,-4) write the equation of the parabola in vertex form.
What is y=(x-2)2-4
Your factory produces lemon scented widgets. You know that each unit is cheaper, the more you produce. But you also know that costs will eventually go up if you make too many widgets, due to the costs of storage and production. The guy in accounting says that your cost for producing x thousand units a day can be approximated by the formula C = .04x2 - 8.504x+25302. Find the daily production level that will minimize your costs.
106.3 thousand units per day