Quadratic Functions
Intervals
Polynomial Functions
Advanced Functions
Logarithms & Trig
100
How many real roots will your function have if the discriminant is negative?
NO real roots
100
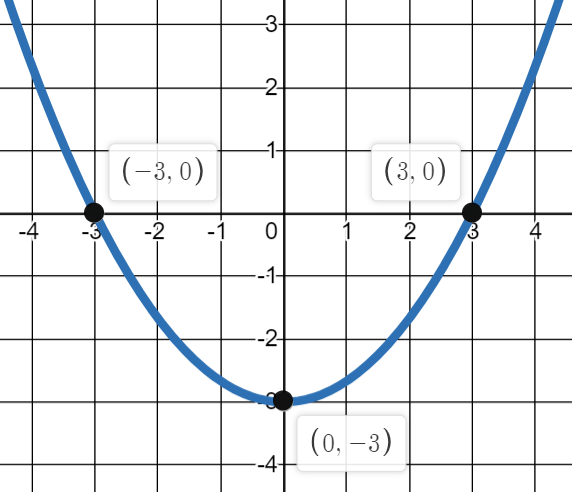
What is the domain of this function?
(-oo,oo)
100
Write the degree, leading coefficient, and end behavior for the following function:
y=-(x-4)^3(x-1)(x+2)
Degree: 5
Leading Coefficient: -1
End Behavior
as x -> infinity, y -> -infinity
as x-> -infinity, y -> infinity
100
Write the equation for each parent function:
A(x)=x^2
B(x)=sqrt(x)
C(x)=root(3)(x)
D(x)=x^3
E(x)=1/x
F(x)=abs(x)
G(x)=ln(x)
H(x)=e^x
100
Evalutate:
log_3(1)
0
200
What can you say about the discriminant for this function?
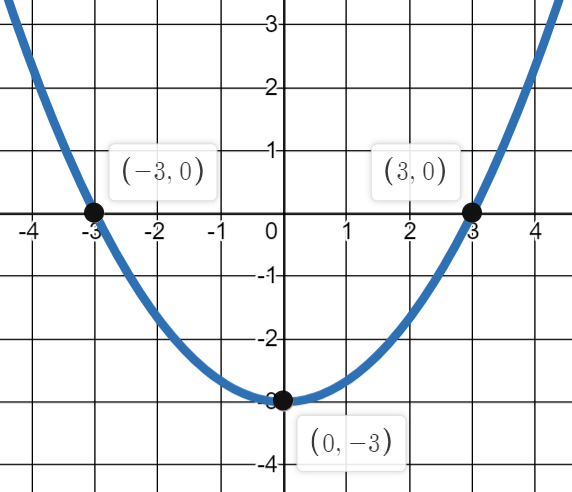
The discriminant must be positive, because the function has two real roots.
200
Write the domain and range for the following function:
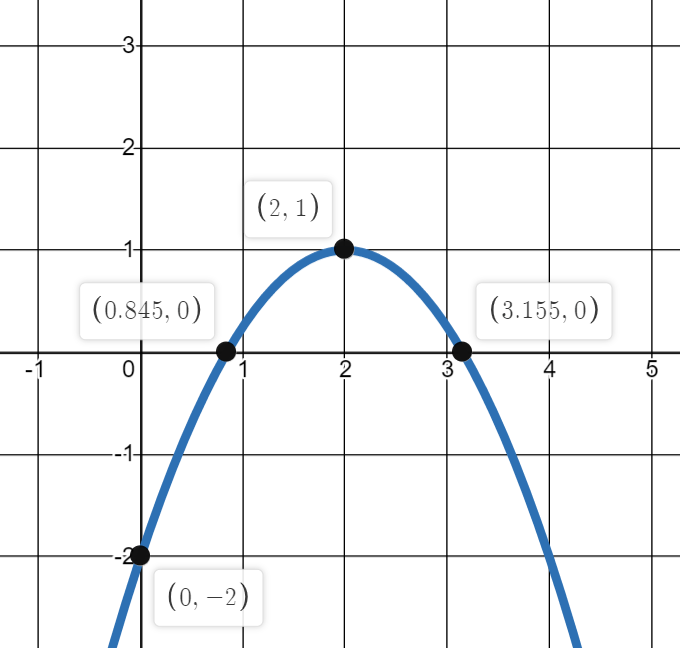
Domain:
(-oo, oo)
Range:
(-oo, 1]
200
Write an equation for the following function:
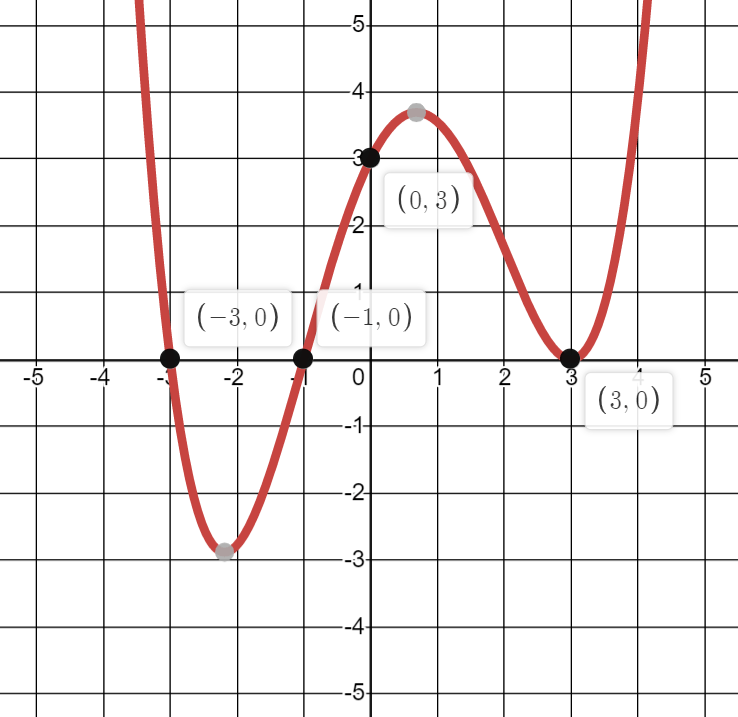
f(x)=1/9(x-3)^2(x+3)(x+1)
200
What transformations have occurred to create the function
g(x)=3e^-x+2
from the function f(x)=e^x ?
The graph of the function has been reflected over the y-axis, dilated vertically by a factor of 3, and been translated up 2 units.
200
Evaluate:
sin(-(5pi)/6)
1/2
300
Write the vertex form equation for this function:
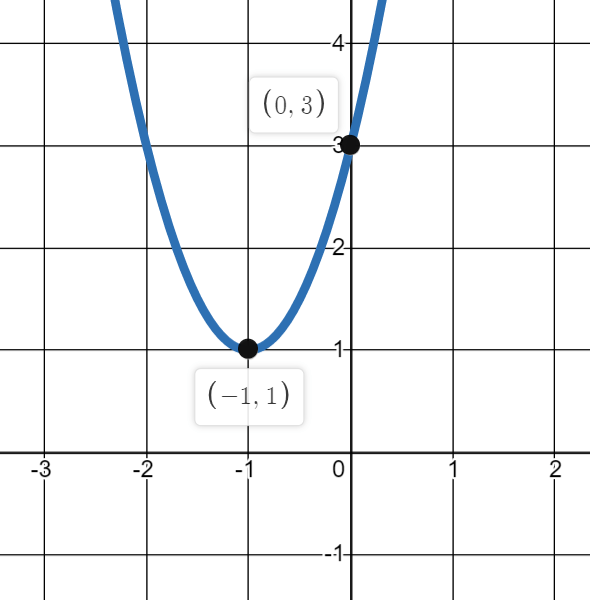
y=2(x+1)^2+1
300
Write the domain and range for this function:
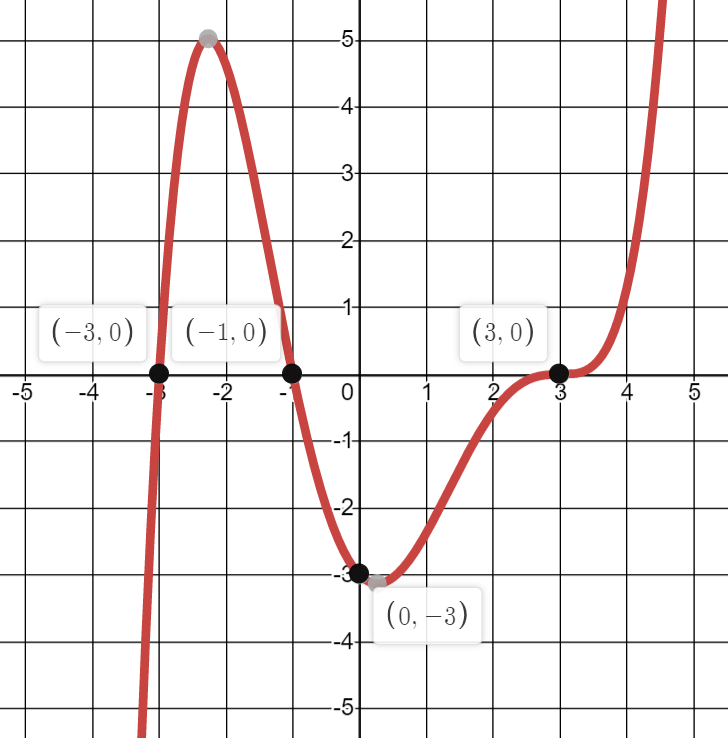
Domain:
(-oo,oo)
Range:
(-oo,oo)
300
Write an equation for the following function:
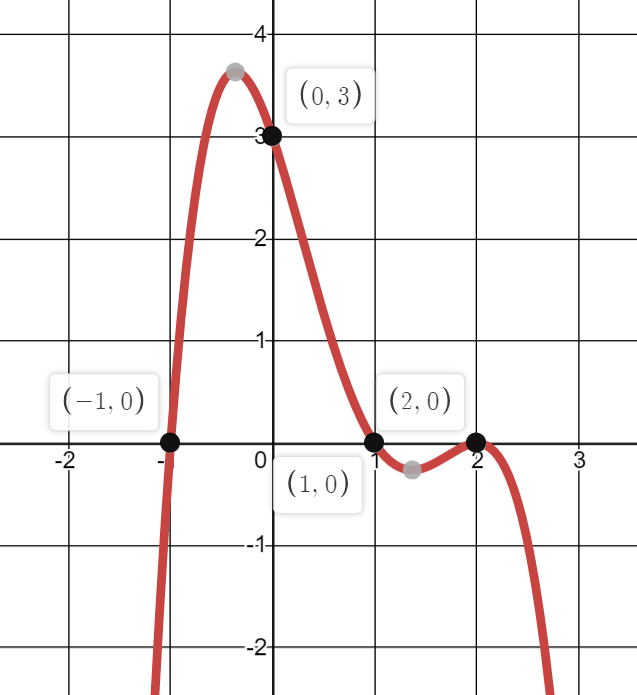
-3/4(x+1)(x-1)(x-2)^2
300
Write the inverse of the following function:
y=-(x-3)^3-5
y=-root(3)(x+5)+3
300
Condense:
log(x^2y)-log(x)+log(y)
log(xy^2)
400
Find the vertex of the following function:
f(x)=x^2-20x+98
(10, -2)
400
What are the increasing intervals for this function?
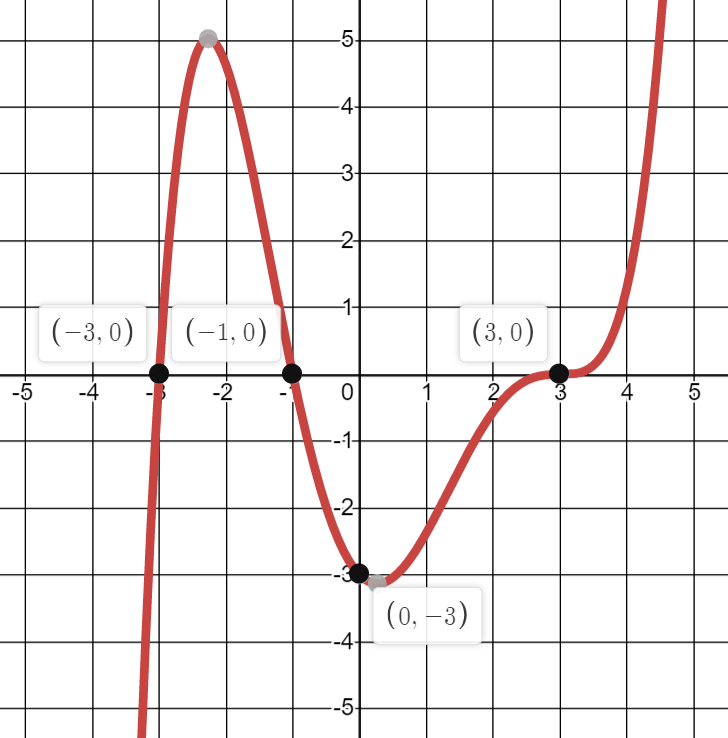
(-oo, -2.25)
and
(0.25, oo)
400
Write a quartic function that...
Has ONLY the roots 3, 4, and 1
Has a y-intercept of 12
f(x)=(x-3)(x-4)(x-1)^2
OR
f(x)=1/3(x-3)^2(x-4)(x-1)
OR
f(x)=1/4(x-3)(x-4)^2(x-1)
400
Write the equation for the following function: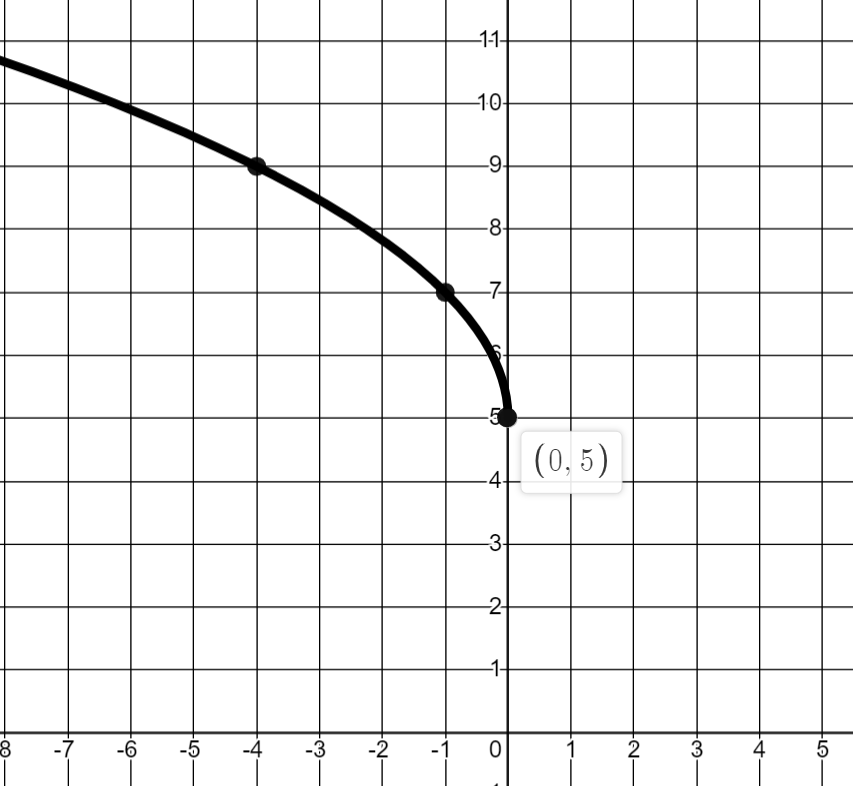
y=2sqrt(-x)+5
400
Name an angle such that sin(theta)=sin((7pi)/9) , but
the angle is NOT coterminal to
(7pi)/9
-(16pi)/9,(2pi)/9,(20pi)/9,...
500
Rewrite the following function in vertex form:
y=x^2-x
y=(x-1/2)^2-1/4
500
For the following function f(x), write the intervals where
f(x) >=0
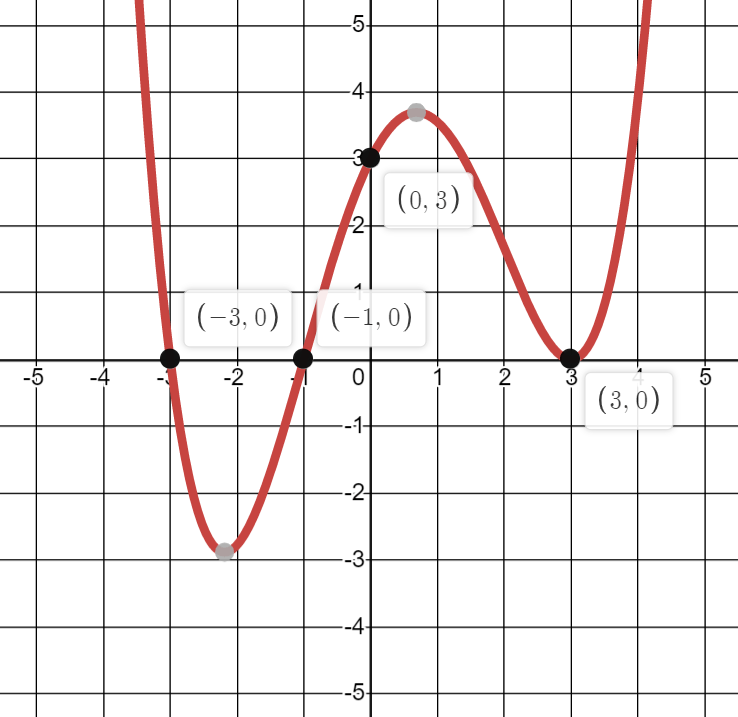
(-oo, -3]
and
[-1,oo)
500
Write a quartic function that...
Has roots 3i and 2-i
Has a y-intercept of 90
y=2(x-3i)(x+3i)(x-2+i)(x-2-i)
or equivalent
500
Solve:
sqrt(x+9)=1+sqrt(x)
Solution:
x=5
Extraneous solution:
x=-8
500
Condense and simplify:
2log(x-2)+log(x-4)-log(x^2-6x+8)
log(x-2)