Functions (General)
Absolute Value, Inverse, Quadratics
Rational, Exponential & Log
Unit Circle & Angles
Trig, graphing &
100
What are examples of where the domain of a function would be undefined (Give two)
square root (negative)
and 0 in the denominator
100
Solve
2 = 3|x-1| -9
x=14/3, -8/3
100
Find average rate of change for f(x) = 3/(x+6)
for [x, x+h]
-3/(x+h+6)(x+6)
100
Find an angle that is coterminal with the following (between 0 and 360 degrees)
750 degrees
AND explain what coterminal means and how to find coterminal angles
30 degrees
terminate at the same location
add 360 if negative
subtract 360 if positive
100
For an inverse trig function to exist:
what has to be true?
1-1
Sin x, cos x, and tan x are not 1-1 so we must restrict them
200
the function:
f(x) = x(x-3)2(x+6)5
Has how many zeros?
What are the multiplicities of each?
What does that mean on a graph?
What is the end behavior
Sketch a graph
3 zeros
0: 1 - cross
3: 2 - bounce
-6: 5 - cross
power: 8 (both up)
200
Find the vertex form of the following:
f(x) = 2x2 +4x + 2
f(x) = 2(x+1)2
200
Find the domain and vertical asymptote of the following:
log4(x-6) +8 = f(x)
Sketch a graph and label the asymptote
x=6
(6,inf)
Desmos
200
Convert 165 degrees to radians
And explain the process of converting from degrees to radians and radians to degrees
11pi/12
multiply by pi/180
or multiply by 180/pi
200
Sketch a graph of:
y=2sinx -4
Make sure to label midline, amplitude, period, and horizontal shifts
Desmos (midline =-4)
300
Find average rate of change f(x) = x^2 +2x -8 for
[5 a]
a+7
300
Given f(x) = −2x4 + 7x3 − 3x2
find the zeros, give their multiplicities, and describe the behavior of the polynomial at the zeros without graphing.
0 (2 - bounces)
1/2 - 1 (crosses)
3 - 1 (crosses)
both negative
300
Sketch the graph and label intercepts, domain/range and the horizontal asymptote.
Explain the transformations
y= -(1/5)(-x-7)
Desmos
300
Find the reference angle of: 120 degrees
and evaluate at sin, cos, tan
60 degrees
2nd quadrant
sqt(3)/2
-1/2
-sqt(3)
300
Sketch the graph of:
y=cos(x/2) + 3
Make sure to label the amplitude, period, midline, and horizontal shift
Desmos (up 3, period of 4pi)
400
f(x) = x2 + 2
g(x) = 1/x
h(x) = x-1
Find f(g(h(x)))
(1/(x-1))2 +2
400
Find the x- and y-intercepts of the graph of the function f(x) = 2|x + 1| − 10.
x=4, -6
y=-8
400
Solve for t:
ln t + ln(t − 1) = ln 6t
t=7
(make sure to check for well-defined)
400
if tan(theta)=3/4 and is in Q3
Find cosec(theta)
-5/3
Use 1 + cot(theta) squared = cosec(theta) squared
400
Recalling (FROM MEMORY)
what does the graph of inverse sin and inverse cos look like
AND
what are the domain and ranges
Sin:
Domain [-1,1]
Range [-pi/2, pi/2]
Cos:
Domain [-1,1]
Range [0,pi]
500
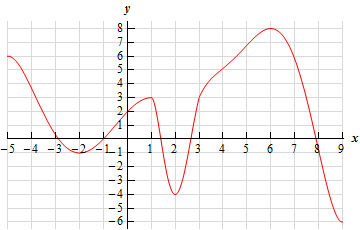
Find the local extrema and explain in terms of increasing and decreasing
Local max:
8 @ x=6
3 @ x=1
min:
-1 @ x=-2
-4 @ x=2
500
Find a domain on which f(x) = (x + 4)2
is one-to-one and non-increasing, then find the inverse of f restricted to that domain.
(-inf, -4]
500
Sketch the graph.
y= (3x2-6)/((x+5)(x-4))
Label all asymptotes and intercepts
Desmos
500
Find all solutions on the interval 0 ≤ θ < 2pi of the following. Give answers in radians.
(a) 2 sin(θ) = −√3
(b) 2 cos(θ) = −1
(a) θ=4pi/3 or 5pi/3
(b) θ= 2pi/3, 4pi/3
500
If sec(t) = −9.65, what is cos(−t)?
-1/9.65