Explain the term
Identify the term
Algebra
Trigonometry
Word problems
100
Subtract
Take away a number or amount from another to calculate the difference
100
A real number that is not divisible by 2.
A real number that can be divided or is divisible by 2.
Odd numbers
Even numbers
100
y=1/4x-7
Identify the slope.
1/4
100
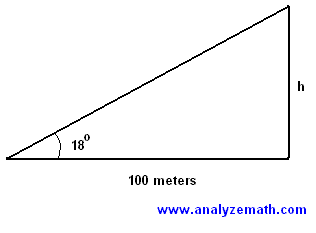
tan(180) = h / 100
100
The sum of two numbers is 72, and one of them is five times the other; what are the two numbers?
x + 5x = 72.
x = 12. 5x = 60
300
Binomial
The sum or the difference of two terms.
300
The number that denotes repeated multiplication of a term, shown as a superscript above that term.
Eg. 34
Exponents
300
x2+5x+6.
Find X
X= -2 or -3
300
The area of a right triangle is 50. One of its angles is 45°. Find the lengths of the sides and hypotenuse of the triangle.
x = 10 / tan(51°) = 8.1
H = 10 / sin(51°) = 13
300
A real estate agent received a 6% commission on the selling price of a house. If his commission was $8,880, what was the selling price of the house?
6% x = 8,880
x = $148,000
500
X intercepts
Y intercepts
The value of x where a line or curve intersects the x-axis.
The value of y where a line or curve intersects the y-axis.
500
The study of lines, angles, shapes, and their properties.
Geometry
500
|a - b| = b - a if b - a < 0
Flase
500
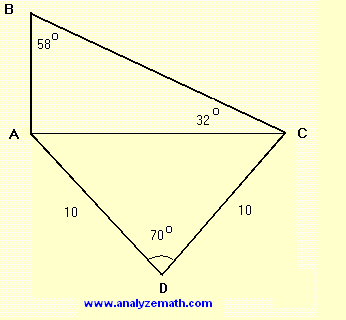
(1/2) AC = 10 sin(35°) or AC = 20 sin(35°)
Note that the two internal angles B and C of triangle ABC add up to 90° and therefore the third angle of triangle ABC is a right angle. We can therefore write
tan(32°) = AB / AC
Which gives AB = AC tan(32°)
= 20 sin(35°)tan(32°) = 7.17 ( rounded to 3 significant digits)
500
If one dimension of the cuboid increases by 1 cm, the surface area of the cuboid increases by 54 cm2. If the second dimension of the cuboid increases by 2 cm, the surface area of the cuboid increases by 96 cm2. If the third dimension of the cuboid increases by 3 cm, its surface area increases by 126 cm2. Find the dimensions of the cuboid.
Dimensions of the cuboid are 9 cm, 12 cm and 15 cm.
800
Diameter
Radius
A distance that passes through the center of a circle and divides it in half.
A distance extending from the center of a sphere to any point on the edge.
800
An algebraic equation in which each term is either a constant or the product of a constant and the first power of a single variable, and whose graph is therefore a straight line. And give an example.
Linear equation
Examples are vary
800
For what value of the constant K would make x2 + 2x = 1 to have two real solutions?
K>-1
800
In a right triangle ABC, tan(A) = 3/4. Find sin(A) and cos(A) .
sin(A) = a / h = 3k / 5k = 3/5
cos(A) = 4k / 5k = 4/5
800
A man is appointed in a job with a monthly salary of a certain amount and a fixed amount of annual increment. If his salary was $19,800 per month at the end of the first month after 3 years of service and $23,400 per month at the end of the first month after 9 years of service, find his starting salary and his annual increment. (Use the matrix inversion method to solve the problem.)
x + 3y = 19800 ---------(1)
x + 9y = 23400 ---------(2)
X = (1/|A|) adj A
|A| = 9 - 3 = 6
x = (178200 - 70200)/6 = 18000
y = (-19800 + 23400)/6 = 600
So, the monthly salary is 18000 and annual increment is 600.
1000
Range
Mean
Median
Mode
The difference between the maximum and minimum in a set of data.
Add up a series of numbers and divide the sum by the total number.
The "middle value" in a series of numbers ordered from least to greatest.
A list of numbers is the values that occur most frequently.
1000
The trigonometric function is equal to the ratio of the side adjacent to an acute angle (in a right-angled triangle) to the hypotenuse.
The trigonometric function is equal to the ratio of the side opposite a given angle (in a right-angled triangle) to the hypotenuse.
A straight line or plane that touches a curve or curved surface at a point, but if extended does not cross it at that point.
Cos
Sine
Tangent
1000
5 (- 3 x - 2) - (x - 3) = - 4 (4 x + 5) + 13
Find X.
All real numbers
1000
tan2(x) - sin2(x) = tan2(x) sin2(x)
tan2(x) - sin2(x) = sin2(x) / cos2(x) - sin2(x)
= [ sin2(x) - cos2(x) sin2(x) ] / cos2(x)
= sin2(x) [ 1 - cos2(x) ] / cos2(x)
= sin2(x) sin2(x) / cos2(x)
= sin2(x) tan2(x)
1000
If 3x−y=12, what is the value of
8x/2y?
A) 212
B) 44
C) 82
D) The value cannot be determined from the information given.
A