Sky's the Limit
Off on a Tangent
Deriving Miss Daisy
Deriving the Meaning
Potpourri
100
The
lim_(x->1) sqrt(5x + 6)
What is
sqrt(11)
100
The slope of the tangent line to the function
f(x) = x^2
at x = 3.
What is 6
100
The derivative of
f(x)=-7x^3+9x^2-4x+3
f'(x)=-21x^2+18x-4
100
For a curve y = f(x), the quantity represented by f'(x) for any point x = a.
What is f'(x) represents the slope of the tangent line to the curve y = f(x) at x = a
100
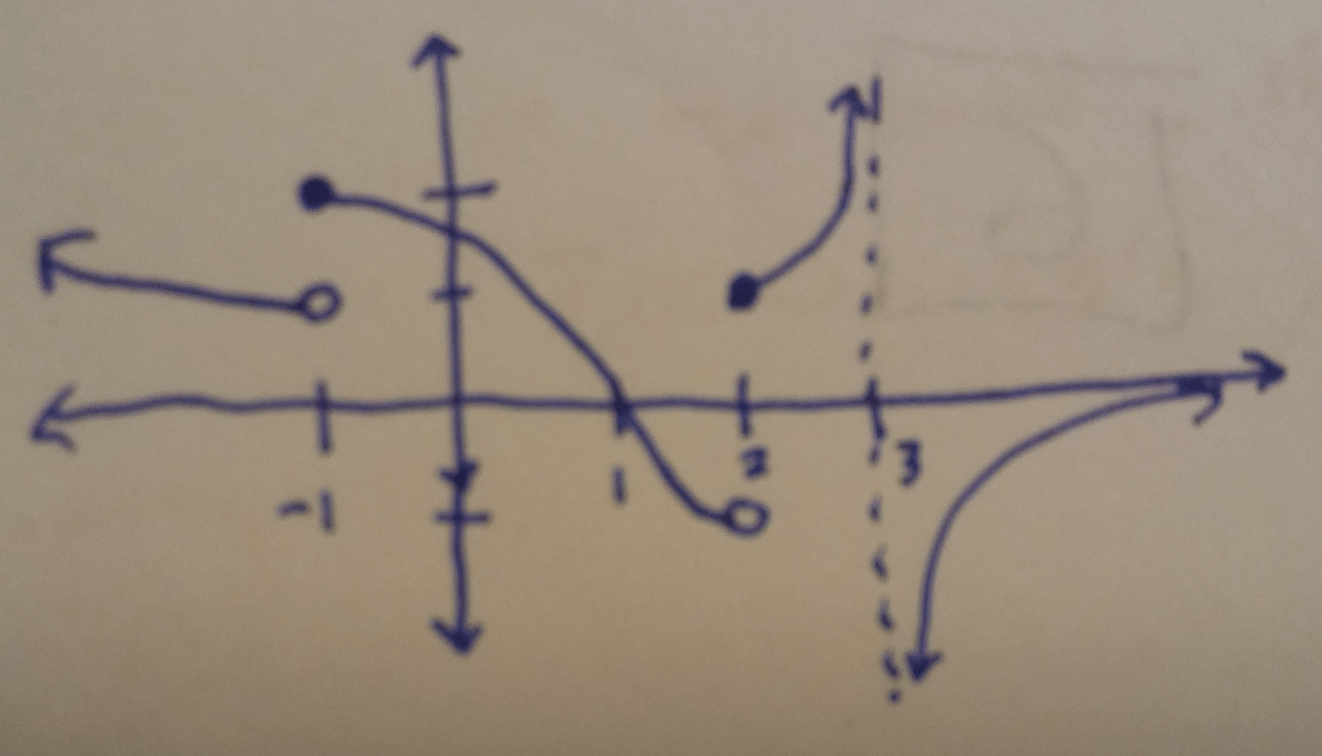For the given graph state the values of x for which the function is discontinuous. For each value state why the function is discontinuous.
What is x = -1 (lim DNE), x = 2 (lim f(x) not = f(2)), x = 3 (lim DNE)
200
The
lim_(x->1) (x^3 -7x^2 + 12x)/(4-x)
What is 2
200
If
lim_(h->0) (f(2+h) - f(2))/h = -3
, the equation of the tangent line to the function f(x) at the point (2,-5).
What is y = -3x + 1
200
Find the derivative
f(x)=(3x^3-7x)(5x^2-3x+10)
What is no horizontal asymptotes
f'(x)=(3x^3-7x)(10x-3)+(5x^2-3x+10)(9x^2-7)
200
The population of a city (in thousands) is given by the function P(t), where t is in years after 2010. Interpret the meaning P'(10) = 2.
In the year 2020, the population of the city is growing at a rate of 2,000 people per year.
200
For the given graph find the following limits: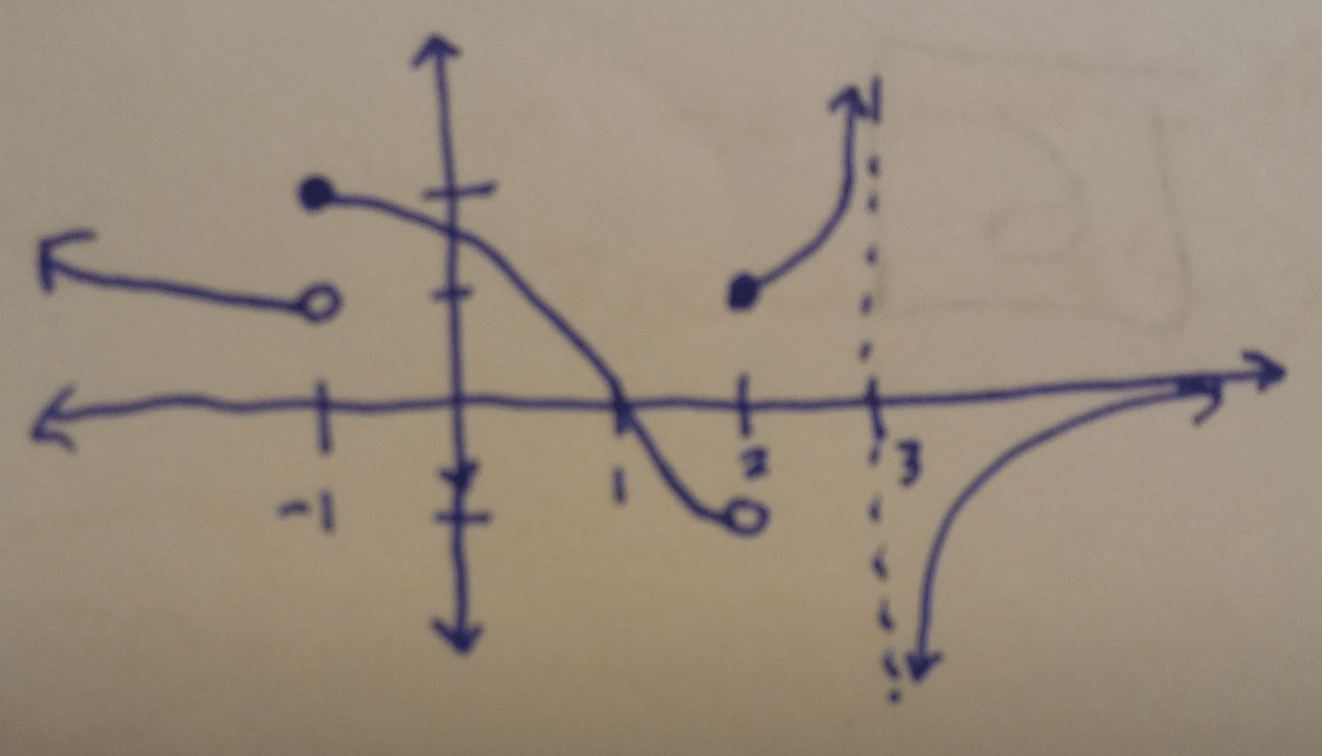
lim_(x->-1^-) f(x)
lim_(x->-1^+) f(x)
lim_(x->-1) f(x)
lim_(x->1) f(x)
lim_(x->3) f(x)
lim_(x->-1^-) f(x)=1
lim_(x->-1^+) f(x)=2
lim_(x->-1) f(x)=DNE
lim_(x->1) f(x)=0
lim_(x->3) f(x)=DNE
300
The
lim_(x->5) (x^2-7x+10)/(x(x-5))
What is
3/5
300
The equation of the tangent line to the function
f(x) = x^2 - 5
at the point (3,4).
What is y = 6x - 14
300
Find the derivative
f(x)=(5x-6)/(2x^2+5x)
f'(x)=(-10x^2+24x+30)/(2x^2+5x)^2
300
The cost C (in dollars) of building a house with size A square feet is given by the function C(A). The meaning of C'(2000) = 100
What is the cost is $100/sq ft to add additional square footage to a house that is already planned at a size of 2000 square feet.
300
A producer and distributer of gift cards produces x boxes of cards per day at an average cost (in dollars) given by:
barC=(6x+8,000)/(2x+300)
Find the average rate of change in the average cost, as production increases from 50 boxes/day to 100 boxes/day.
-$.07 per box
400
The
lim_(x->oo) (6x+8,000)/(2x + 300)
What is 3
400
The equation of the tangent line to the curve y = f(x) at x = 3, if f'(3) = 5 and f(3) = -1
What is y = 5x - 16
400
Find y' for
3x^5 + 2y^4 + y = 37
at the point (1,2)
-3/13
400
Fertilizers can improve agriculture. Research of corn production in Kenya found that the average value, y = f(x), in Kenyan schillings of the yearly corn production from an average plot of land is a function of quantity, x, of fertilizer used in kg. Interpret the meaning of f'(20) = 350.
The average value of yearly corn production will increase at a rate of 350 Kenyan schillings/kg when 20 kg of fertilizer is used.
500
The
lim_(x->oo) (x^4 - 1)/(x^5 + 2)
What is 0
500
The equation of the tangent line to the curve
f(x) = 3/(2x+1)
at the point (1,1)
What is
y = -2/3 x + 5/3
500
The director of the personnel office of a large company has determined that the function N(x) approximates the relation between the number N of applicants applying for an accounting position and the amount of dollars x (in hundreds) it advertises as benefits. Interpret the meaning of N(42) = 340 and
N'(42)=66
When accounting firm advertises a job with $4,200 in benefits, there will be 340 applicants, and the number of applicants is increasing by 66 applicants per $100 increase in benefits.