CHAPTER 1
CHAPTER 2
CHAPTER 3
CHAPTER 4
CHAPTER 5
CHAPTER 5 PT.2
100
-DOMAIN AND RANGE-
Find the domain and range of the graph below.
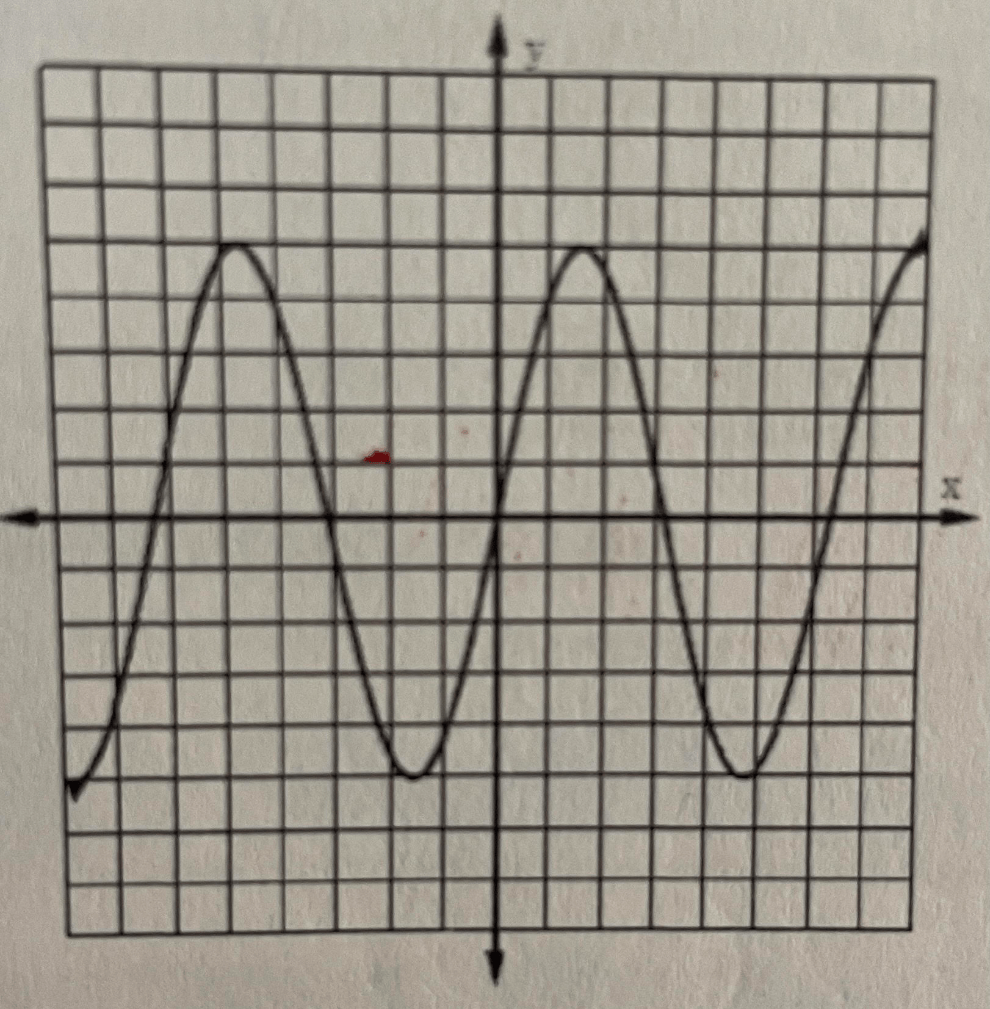
-DOMAIN AND RANGE-
domain= (negative infinity, positive infinity)
Range= [-5,5]
100
-TYPES OF SYMMETRY-
Use the graph below to determine if the relation is symmetrical to the x-axis, y-axis, and the origin. Confirm your answer algebraically using the function below.
y2-x2=1
-TYPES OF SYMMETRY-
Symmetrical to the...
x-axis, y-axis, and origin
100
-GRAPHING FUNCTIONS-
Find the domain, range, and transformations of the following equation.
f(x)=-4/x+3
-GRAPHING FUNCTIONS-
Domain: (negative infinity, -3] U [-3, positive infinity)
Range: (negative infinity, 0) U (0, positive infinity)
Transformations: Vertical Stretch by 4, reflection across y-axis, left 3
100
-POWER FUNCTIONS-
Find the symmetry of the following function and graph.
f(x)=-2x5
-POWER FUNCTIONS-
symmetry: orgin
100
-DIVIDING POLYNOMIALS WITH LONG DIVISION-
Divide using long division
x2-x-5squart(x4-5x3+x2+20x-10)
-DIVIDING POLYNOMIALS WITH LONG DIVISION-
=x2-4x+2+2x/x2-x-5
100
-RATIONAL FUNCTIONS AND THEIR GRAPHS-
Find the asymptotes of the function and graph below
f(x)=x+1/x-5
-RATIONAL FUNCTIONS AND THEIR GRAPHS-
Horizontal Asymptote: y=1
Vertical Asymptote: x=5
200
-ZEROS AND Y-INTERCEPTS ALGEBRAICALLY-
Find the zeros and y-intercepts of the following equation, f(x)= x4-5x2+4
-ZEROS AND Y-INTERCEPTS ALGEBRAICALLY-
Zeros: x=2,-2,-1,2
Y-Int: y=4
200
-EVEN/ODD FUNCTIONS-
Using the function below describe algebraically if the function is even, odd, or neither, and describe the symmetry.
f(x)= squart(x2-4)
-EVEN/ODD FUNCTIONS-
even; symmetrical about the origin
200
-OPERATIONS WITH FUNCTIONS-
Given f(x) and g(x) below, find each new function and state its domain
f(x)= x2+9 g(x)=squart(x)
Using the information above find (f/g)(x)
-OPERATIONS WITH FUNCTIONS-
f-1(x)= x5/2+9x1/2/x
200
-POWER FUNCTIONS WITH NEGATIVE EXPONENTS-
Find the discontinuities of the following function and graph.
f(x)=4x-2
-POWER FUNCTIONS WITH NEGATIVE EXPONENTS-
Discontinuities: x=0, infinite
200
-THEOREMS-
Using the factor theorem and the function below, determine which binomials are factors of the given function
f(x)=3x3+13x2-32x-12
(x+6) (x-2) (x+4)
-THEOREMS-
(x+6)= yes
(x-2)= yes
(x+4)= no
200
-OBLIQUE ASYMPTOTES-
Find the equation of the oblique asymptote for the function below
f(x)=x3+3x2/x2+2x-3
-OBLIQUE ASYMPTOTES-
y=x+1
300
-CRITICAL POINTS/INCREASING & DECREASING BEHAVIOR-
Find the Relative Minimums and Maximums, and the increasing and decreasing intervals for the function and graph below.
f(x)= -x3-5x2-3x+4
-CRITICAL POINTS/ INCREASING & DECREASING BEHAVIOR-
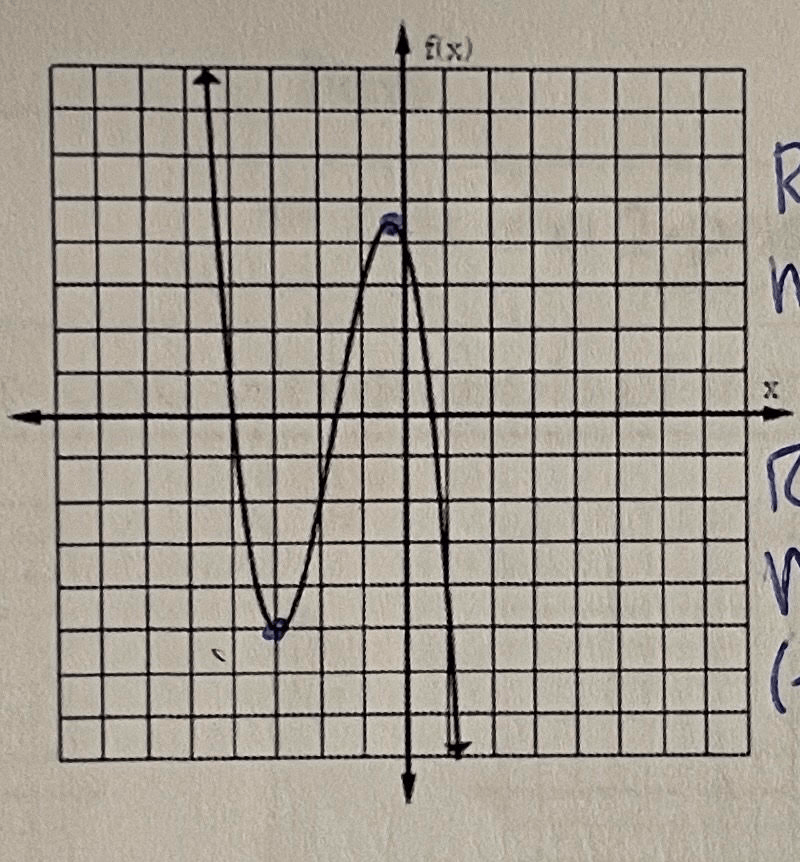
Rel.Minimum:(-3,-5),Rel.Maximum (-0.33,4.48)
Increasing Interval:(-3,-0.33)
Decreasing Interval: (negative infinity,-3) (-0.33, infinity)
300
-AVERAGE RATE OF CHANGE-
find the average rate of change for the function below
f(x)=-x4+3x2-17;[-2,5]
-AVERAGE RATE OF CHANGE-
-78
300
-COMPOSITION OF FUNCTIONS-
Given f(x) and g(x) below, find each function and state its domain
f(x)= 3-x. g(x)=x/x+1
Find (f o g)(x)
-COMPOSITION OF FUNCTIONS-
=2x+3/x+1
Domain= x can not equal -1
300
-POWER FUNCTIONS WITH RATIONAL EXPONENTS-
Find the end behaviors of the following function and graph.
f(x)=sqaurt(27-x3)
-POWER FUNCTIONS WITH RATIONAL EXPONENTS-
As x> 3 > f(x) approaches 0
As x> negative infinity, f(x)> positive infinity
300
-FINDING RATIONAL ZEROS-
Using the rational zero theorem, list all the possible 0's, and then find the actual zeros using the equation below.
f(x)=x4+3x3-7x2-27x-18
-FINDING RATIONAL ZEROS-
possible 0's: +/- 1, +/-2, +/-3, +/-6, +/-9, +/-18
x={-2,-1,+/-3}
300
-SLANT ASYMPTOTES-
Find the slant asymptote of the following equation.
f(x)=x2-9/x
-SLANT ASYMPTOTES-
Slant Asymptote: y=x
400
-END BEHAVIOR-
Find the end behavior of the following graph
As x > positive infinity, f(x) > 0
As x > negative infinity f(x) > 0
400
-IDENTIFYING TRANSFORMATIONS-
For the function below, identify both the parent function and the transformations
f(x)= l 3(x+5) l -2
-IDENTIFYING TRANSFORMATIONS-
Parent: Absolute Value, l x l
Transformations: horizontal compression by 1/3, left 5, down 2
400
-FINDING INVERSE FUNCTIONS-
Determine if f(x) has an inverse of the function below, if yes, find f1(x). State any restrictions in the domain.
f(x)=-squart(x+2)-7
-FINDING INVERSE FUNCTIONS-
f-1x=(-x-7)2-2
400
-POLYNOMIAL FUNCTION-
Using the leading term, give the end behavior of the following function
f(x)= 1/2x3+10x2-4x+2
-POLYNOMIAL FUNCTION-
As x> positive infinity > f(x) positive infinity
As x> negative infinity, f(x)> negative infinity
400
-IRRATIONAL ZEROS-
Find all zeros using the function below
f(x)=3x3-15x2-4x+20
-IRRATIONAL ZEROS-
x= +/- 2 sqaurt(3)/3, 5
400
-POLYNOMIAL INEQUALITIES/TEST INTERVALS-
Solve each inequality for the equation below and use the number line below to test intervals
x4-26x2+25 (is greater than or equal to) 0
-POLYNOMIAL INEQUALITIES/TEST INTERVALS-
(negative infinity,-5]U[-1,1]U(5, positive infinity)
500
-CONTINUITY-
find the discontinuities in the following graph
-CONTINUITY-
Infinite Disc: x=2
Removable Disc: x=4
500
-TRANSFORMATIONS(from word form to equation)-
Using the graph below find the parent function. Then write an equation for the function using the words below
*Translate 3 units up and 8 units to the right, and horizontally compressed by a factor of 1/4, and reflected across the y-axis
-TRANSFORMATIONS(from word form to equation)-
Parent: Square Root; f(x)= squart(x)
Transformed Equation:
f(x)= squart(-4(x-8) +3
500
-VERIFYING INVERSES-
Find the inverse of the function below. Verify graphically.
f(x)=3x-6
-VERIFYING INVERSES-
f-1(x)=1/3x+2
500
-GRAPHING POLYNOMIAL FUNCTIONS-
Find the relative minimum and the relative maximum of the following function and graph.
f(x)=x4-x3-4x2+1
-GRAPHING POLYNOMIAL FUNCTIONS-
Relative Minimum: (-1.09,-1.05) (1.84, -7.31)
Relative Maximum: (0,1)
500
-COMPLEX ZEROS-
Find all zeros of the polynomial function below. Simplify all irrational and complex solutions.
f(x)=x4-4x2-12
-COMPLEX ZEROS-
x= +/- squart(6), +/- i squart(2)
500
-RATIONAL INEQUALITIES/TEST INTERVALS-
Solve each inequality for the equation below and use the number line below to test intervals
9/x-4 (is less than or equal to) 8/x-3
-RATIONAL INEQUALITIES/TEST INTERVALS-
(negative infinity, -5]U(3,4)