How do spirals, spots, and stripes appear in nature?
 They appear from a chemical phenomenon called the reaction-diffusion effect.
They appear from a chemical phenomenon called the reaction-diffusion effect.
What is the most commonly known sequence found in nature?
/https://tf-cmsv2-smithsonianmag-media.s3.amazonaws.com/filer/3a/70/3a70f58d-dabc-4d54-ba16-1d1548594720/2560px-fibonaccispiralsvg.jpg)
Fibonacci Sequence
What were Galileo Galilei's beliefs?
He believed that nature was inherently mathematical and that math was the language of nature.
What is Symmetry's definition?
 A pattern found in all living things.
A pattern found in all living things.
Who discovered Math in nature?
Leonardo de Pis (Fibonacci).
What are some examples of geometry in nature?
Stars on starfish, circles in tree trunks, hexagons in beehives, triangles in leaves, flowers, animals' ears, noses, and teeth.
What is the most common form of symmetry in nature?

Bilateral symmetry.
What were Fibonacci's beliefs?
:max_bytes(150000):strip_icc()/Leonardo-Pisano-Fibonacci-f9d544e22fb147fea36f99b4dcd77f50.jpg)
He believed mathematical patterns exist throughout nature. Teachers use the Fibonacci Sequence to teach STEM.
What is Bilateral symmetry?
The property of being divisible in symmetrical halves.
What is the connection between math and the natural world?

Nature seems to organize itself according to mathematical laws.

This means they all share the same center but each circle has different radii. Meaning all circles are different sizes within one another.
What are Fractals in nature?

A fractal is a self-similar, repeating shape. If you were to zoom in our out, the shape would be the same.

He believed that there are two chemicals inside an animal's body and concentrations show where patterns form on the animal. His mathematical equations can explain the way these chemicals react and how patterns form.
How many types of symmetry are there?
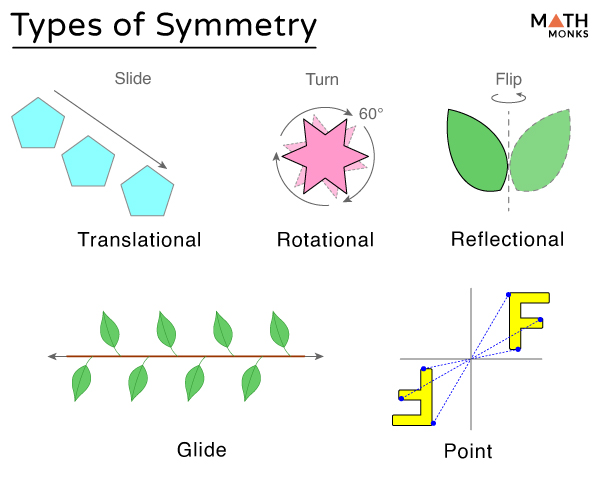
There are five types: Transitional symmetry, rotational symmetry, reflectional symmetry, glide symmetry, and point symmetry.
What is the origin of math?

From 2000 bc to 1800 bc, Mesopotamians and ancient Egyptians began to use and observe patterns and geometry in nature
How does geometry appear in everyday life?

Geometry is the most influential branch of mathematics. The most common applications are lines on a map, shapes in signs, robotics, fashion, and much more.
Why were patterns noticed in nature?

This is because of the chemical interactions and law of nature (such as natural selection).
What are John A. Adam's beliefs?

He is a British-American mathematician who is known for his patterns in nature and mathematical modeling of growth patterns of cancer and blood vessels.
Why is symmetry so important in nature?

Symmetry is so important because of evolution's preference for simple algorithms. Symmetry abounds in nature, often in its most beautiful forms.
Why is math in nature important?
It is important to apply logic, learn from mistakes, think creatively, work collaboratively, and communicate ideas.
What shape is not found in nature, and why?

A mathematical circle doesn't exist in nature because a) it is a two dimensional object and b) shapes in nature are quantized.
What are the four most common types of sequences?
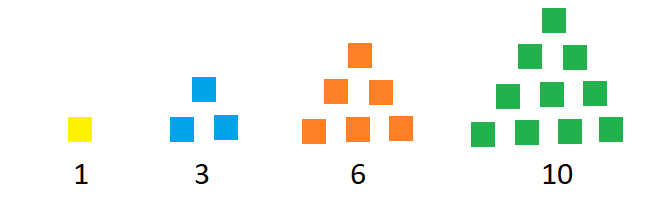
The four most common types are; Arithmetic sequence, geometric sequence, harmonic sequence, and Fibonacci Numbers.
What are Benoit Mandelbrot's beliefs?

He developed a theory of "roughness and self-similarity" in nature.
How does symmetry occur in nature?
This occurs wherever mirror images are repeated.
How essential is mathematics in the natural world?

Both genetics and evolution are heavily governed by mathematics. By using mathematical models, we can understand why population numbers and physical characteristics within populations fluctuate and fixate.