Functions
Rational Expressions
& Transformations
& Transformations
Exponential Functions
Trigonometry
(Special Angles)
(Special Angles)
Trigonometric Functions
100
If f(x)=3x-2x2, then determine f(-2).
What is: f(-2)=-14
100
State the restrictions on the following expression: x2+10x+16/x2-9.
What is: x≠3, -3
100
A colony of E. coli bacteria has an initial population of 500 cells. This population of bacteria seems to decrease by a factor of 5 every day. Determine an equation that relates the declining population, P, to the time, t, in days.
What is: P=500(5)t
100
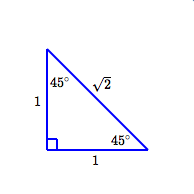
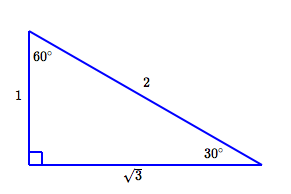
Label all the sides and angles of the two special triangles we learned in this unit.
What is:
100
Determine the amplitude, period, and equation of the axis for the following function:
y=3cosx-4
What is: Amplitude=3, Period=360°, Equation of the Axis is y=-4.
200
Is the graph below a function? What is the model's domain and range?
What is: yes, it is a function; it passes the vertical line test.
D={x∈R|x≠0}
R={y∈R|y≠0}
200
Find the equation for the inverse function of f(x)=√x + 37.
What is: y=(x-37)2
200
Simplify the following and state your answers using only positive exponents:
(25a-4b5/5b3)3
What is: a12/125b6
200
Convert the following degrees into radian measure:
285°
What is: 19π/12
200
Describe the transformations that would be applied to f(x)=sinx to obtain the following function:
g(x)=5sin(3x-30°)+5.
What is:
- vertically stretch by a factor of 5
- horizontally compress by a factor of 1/3
- phase shift 10° right
- translate 5 units up
300
Expand and simplify the following:
(10-√12) (2-√12).
What is: 32-24√3
300
Simplify the following expression and state its restrictions:
(x2-11x+10/x+5)/(2x-2/2x+10).
What is: x-10, x≠-5, 1
300
An exponential function has an asymptote of y=-4, a y-intercept of 7, and the curve passes through the point (1, 18). Determine an equation to model this function in the form y=a(b)x+c.
What is: y=11(2)x-4
300
Use special triangles and the CAST rule to find the exact value of sec 210°. Include a diagram.
What is: -2/√3
300
Sketch one cycle for the following trigonometric function and state its domain and range:
y=-2cos[1/2(x-90°)]+2
What is:
D={x∈R}
R={y∈R|2≤y≤4}
400
Solve the linear-quadratic system:
y=6x-10 and y=3x2-10x+11.
What is: the solutions are (3,8) & (7/3,4).
400
Graph the following function and describe the transformations that have occurred to its base function:
f(x)=-√(4x+12) -3
What is:
- reflection in the x-axis
- horizontally compressed by a factor of 1/4
- translate 3 units left
- translate 3 units down
400
Graph the following exponential function and describe the transformations that have occurred to its base function:
y=4(2)4(x-5)+4
What is:
- vertically stretched by a factor of 4
- horizontally compressed by a factor of 1/4
- translate 5 units right
- translate 4 units up
400
Triangle ABC has ∠A=55°, b=6.3 m, and a=11.4 m. Determine if this is an ambiguous case. Solve the triangle(s).
What is: not an ambiguous case.
∴∠B=26.5°, ∠C=98.5°, c=13.8m.
400
Prove the following identity:
(1+cosx/sinx)+(sinx/1+cosx)=2cscx
What is:
500
The coffee company, Keurig, is selling their coffee for $1.90 a cup. At this price, it sells about 150 cups per day. Keurig employees predict that for every 5 cent decrease in price, the sales of coffee will increase by 15 cups per day. Solve for the coffee price that will maximize Keurig's revenue.
What is: the coffee price that will maximize Keurig's revenue is $1.20.
500
Determine a simplified expression for the perimeter of the rectangle with a length of 3x-3/6x and a width of 2x+1/3x. State any restrictions.
What is: 7x=1/3x, x≠0
500
Thorium (Th) is a radioactive element. It's waste product is determined to have a half-life of 500 years. A sample collected my radiologists has a mass of 230 mg. What mass of thorium waste remains after 3500 years? Round your answer to two decimal places.
What is: the mass of the thorium waste will be approx. 1.80mg after 3500 years.
500
Nico is standing in front of a building at a small urban complex, ready to walk to another building a few blocks away. The complex is designed so that its main pathway faces north toward a tall building. From the starting point of the pathway, the angle of elevation to the top of the tall building is 7°. From a point 500 meters perpendicular to the pathway, the angle formed by the starting point of the pathway and the tall building is 60°. What is the height of the building?
What is: the height of the tree is approx. 101m in height.
500
James gets on a Ferris wheel and is 4 meters from the ground. When he is at the top of the ride, he determines that the height from the ground is 28 meters. He also ensures that it takes 120 seconds for the wheel to make one rotation. Determine a cosine function to model James's height above the ground and sketch 2 rotations of the ride.
What is: