How many of the 26 letters in the English alphabet appear in both of the words 𝐼𝑁𝑇𝐸𝐺𝑅𝐴𝐿 and 𝐷𝐸𝑅𝐼𝑉𝐴𝑇𝐼𝑉𝐸?
5
Grogu and Mando are hiding away on the planet Sorgan. Grogu’s hut can be modeled by the pyramid bounded
by the plane 2x + 3y + 6z = 12 and the coordinate planes. What is the volume of Grogu’s hut?
8
Consider the functions f (x) = ax + 4 and g(x) =−x + 10. If f (g(x)) = g( f (x)), determine the value of a.
1/5
What is the smallest positive integer n such that 4 √n+ 2023 is an integer?
Solution: 378
Given the system of linear equations 5𝑥 + 2𝑦 = 11
𝑥 − 3𝑦 = 9
What is the value of 2𝑥 + 5𝑦 ?
-4
A square with area 18 is rotated about one of its diagonals to create a solid. What is the volume of this
solid?
18𝜋
If the acute angle between the planes 9x + 6y−2z = 7 and−8x + 4y + z = 11 is θ, what is cos(θ)?
50/99
Find the number of asymptotes the function f (x) =x3 −8/x2 −4 has.
2
A circle in the coordinate plane has its center at (0,0) and passes through the points (3,a) and (a−2,4). What is a?
Solution: 11/4
Given the quadratic equation 𝑦 = −5𝑥2 + 30𝑥 + 7, what is the maximum value of y ?
52
A square with area 18 is rotated about one of its diagonals to create a solid. What is the surface area of
this solid?
18𝜋√2
What is the maximum value of 3-x^2·93x/27 ?
36
Find the sum of x for the following equation: log2 (x−1) + log4 (x−4) = 2
5
The areas of three triangles form an arithmetic progression. If one of the triangles has side lengths 8, 15, and 17, and another one of the triangles has side lengths 7, 24, and 25, what is the sum of the possible areas of the third triangle?
Solution: 216
How many prime numbers are between 50 and 100 ?
10
The function 𝑓(𝑥) = |𝑥| + 1/|𝑥+1| has two local minima at the points (𝑎, 𝑏) and (𝑐, 𝑑). Compute 𝑎𝑏𝑐𝑑.
0
Which of the following is equal to 1−cos 2θ?
2 sin2 θ
A line passing through the point (0, 4) intersects the graph of y= x2 + 1 in two distinct points. The positive difference in x-coordinates of these two points is 6. Compute the positive difference between the points’ y-coordinates.
12√6
Suppose that a rectangle ABCD satisfies AB : AC = 8 : 17. If the area of ABCD is 24/5 , what is the length of BC?
Solution: 3
What are the coordinates of the x intercept of the rational function 𝑓(𝑥) =10-2x/𝑥−6?
(5,0)
Numerically, the area of a rectangle with integer side lengths is 2 greater than its perimeter. Find the sum of all possible values for the length of the shorter side of the rectangle.
7
Max’s function is f(x) = (x−2)2 + 1. Evaluate f(f(4)).
10
A quadratic function g passes through the points (1, 3), (4, 7), and (5, 11). Find the value of g(2).
3
A high school math team has 10 different students and 15 identical cookies to hand out. If each student receives at least one cookie, and no student gets more than two cookies, in how many ways can the cookies be distributed?
Solution: 252
In the figure below the area of the trapezoid ABCD is 90. Also AB is 12 , BE is 9 , CD is 𝑥 and DE is 𝑦. Find the value of 2𝑥 + 3𝑦.
28
Consider the polynomial x3−9x2 + tx + 165, where t is a real number. At what value of t does this polynomial have three distinct roots in arithmetic progression?
-37
θ is−π/4 . Find the value of sin θ + cos θ.
0
Find the coefficient of the x2y term of the function
f(x,y) = (2x−5y)3
.
-60
6. A farmer must bring water to her sick cow. The farmer is at coordinates (0,12) and the cow is at coordinates (10,8). The river where she will fill her bucket from is the line y= 0. At which point (x,0) along the river should the farmer walk towards to yield the shortest round trip to the cow?
Solution: x= 6
Solve 3𝑏𝑥 + 9 = 4(3𝑥 − 𝑏) + 2 for 𝑥.
-4b+7/3b+12
There are eight crewmates and two impostors on a ship. Every second, one person is randomly thrown off the ship. What is the probability that before the ship is emptied, there are always more crewmates than impostors on board?

3/5
The monthly rent for an apartment in Atlanta is $2600 less than the cost of renting the apartment for 3 months. How much does it cost to rent the apartment for a year?
$15600
Alejandro works at a factory where he earns $9 per hour. He currently has $300. What is the least amount of integer hours he must work to be able to afford a $500 TV?
23
Let p and q be the roots of x2 −6x+ 4 with p>q. What is p2 −q2?
Solution: 12√5
Two cards are drawn, without replacement, from a standard deck of playing cards. Find the probability that both are red.
25/102
The number 1234312 has three distinct prime factors. Compute their sum.
836
Two sequences are given below with sums of A and B. What is the value of A−B?
2 + 4 + 6 + 8 + 10 +. . . + 198 + 200= A
1 + 2 + 3 + 4 + 5 +. . . + 99 + 100= B
5050
Scott starts at 𝐴 and looks up to 𝐷 at an angle of elevation of 30∘. He walks forward a distance of 20 feet to point 𝐵. From 𝐵, he looks up again to 𝐷 at an angle of elevation of 45∘. What is the distance 𝐷𝐶?
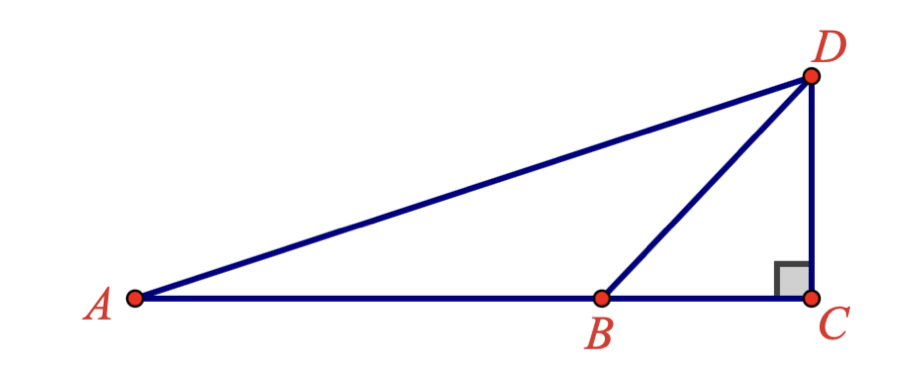
10(√3 + 1)
Suppose an and b are irrational numbers such that a3 ≈31.00627 and b3 ≈20.08554. What is
(a−b) (a+ b)2 −ab , rounded to the nearest hundredth?
Solution: 10.92
How many six digit multiples of 5 can be formed from the digits 1, 2, 3, 4, 5, and 6 using each of the digits exactly one time?
120
An SRS of 576 American households found an average of $475 spent on groceries monthly. It is known that the true population standard deviation of the amount spent on groceries monthly for all American households is $96 exactly. What is the 90% confidence interval for the true mean amount spent on groceries monthly for American households? Round the appropriate critical value to 3 decimal places.
475±6.580
Jaden brings in one complete cake. He then brings in 2 half cakes. He then brings in 3 quarter cakes. He continues to bring in cakes increasing in quantity by one but decreasing in size by a half. What is the total amount of cake he brings in?
4
Ohm’s Law states 𝑉 = 𝐼𝑅 where 𝑉 is the voltage, 𝐼 is the current, and 𝑅 is the resistance in a circuit. If the resistance is (2 − 3𝑖) and the voltage is (21 + 𝑖), what is the current?
3 + 5𝑖
A 60 person party wants to order pizza. There are 40 people who want pepperoni, 16 who want cheese, and 50 who want supreme. A total of 40 people want at least two kinds of pizza and 12 want all three kinds. How many people don’t want any pizza?
Solution: This is a direct application of the inclusion-exclusion principle. The number of people who want pizza is 40 + 16 + 50−(40 + 2 ∗12) + 12 = 54, so 6 people do not want pizza.
There are 93 sixth graders and 108 seventh graders entering a raffle. In each grade, the number of dog owners is twice the number of students who do not own a dog. What is the probability that a seventh grader who does not own a dog wins the raffle? Express your answer as a common fraction.
12/67
There are 6 boxes, indexed 1,2,…,6, each of which contains 64 balls where each ball is either blue or red. The number of blue balls in box 𝑛 is equal to 2n. A box is randomly selected and a ball is randomly selected from the box. Given the ball is red, the probability that the 4th box was chosen is 𝑚/𝑛 in simplified form. What is 𝑚+𝑛?
51
The last question is usually easy. What is cos 90?
(A)−1
(B) 0
(C) 1
(D) √2/2
(E) NOTA
E
How many arrangements of the letters of the word “GEMINI” are there?
360
Given that f(x) = 4x3 −6x2 + 4x−1, what is
f(2) + f(3) +···+ f(100)?
Solution: 99999999
If f(x) = -4x - 5 and g(x) = 3 - x, what is g(-4) + f(1)?
-2