Random
More Systems!
Systems of Equations
Addition and Subtraction
Matrix Multiplication
100
Identify element a23 from A =
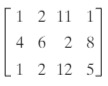
2
100
Javiar wrote an equation to represent the following, 3 pens and 2 pencils cost $3.50 as 3x+2y = 3.50
What do x and y represent? (Define the variables)
x is the cost of a pen
y is the cost of a pencil
100
What is the matrix equation of
{[2x+3y=8], [4x-y=5]}
[[2,3],[4,-1]][[x],[y]]=[[8],[5]]
100
What is the rule for determining if two matrices can be added or subtracted together?
The matrices have to be the exact same dimensions (equal number of rows and columns)
100
Can the following matrices be multiplied together? How do you know?
[[1,2],[3, 4],[5, 6]] [[1,2, 3],[4, 5, 6]]
Yes, because the first matrix is a 3x2, and the second matrix is a 2x3. Since the second matrix has the same number of rows, as the first one has columns (2), these matrices can be multiplied together.
200
Find the determinant:
[[6,4],[-9,3]]
54
200
3 pens and 2 pencils cost $3.50
4 pens and 3 pencils cost $4.86
Write a matrix equation to represent the situation
3 2 x = 3.50
4 3 y 4.86
200
What is the solution, x=? and y = ?, of the matrix equation
[[5,3],[2,1]][[x],[y]]=[[-5],[1]]
[[8],[-15]]
200
Simplify the following matrices based problem: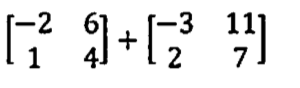
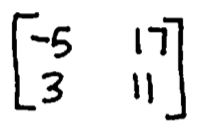
200
Solve the following operations:
2[[1,-2],[-3, 4],[5, -6]] + [[-7,8],[9, -10],[-11, 12]]
[[-5,4],[3,-2],[-1,0]]
300
What is the inverse of
[[3,2],[4,1]]
[[-1/5,2/5],[4/5,-3/5]]
300
3 pens and 2 pencils cost $3.50
4 pens and 3 pencils cost $4.86
Write the augmented matrix for the system and solve for the cost of each pen and each pencil
3 2 3.50
4 3 4.86
pen = .78
pencil = .58
300
What is the solution of
[[-6,-3],[8,4]][[x],[y]]=[[144],[-64]]
no solution
300
Given Matrix X and Matrix Y. What is Y-X?
Matrix X=
[[2,-3],[-1,4]]
Matrix Y=
[[-4,1],[3,-2]]
[[-6,4],[4,-6]]
300
What is AxB?
Matrix A=
[[1,1],[1,1]]
Matrix B=
[[0,3],[4,4]]
[[4,7],[4,7]]
400
How do you know if two matrices are inverses?
When you multiply them together, their product equals an Identity matrix.
400
Write the system of equations associated with the augmented matrix
[[3, 4, 8, 9],[-2, -1, 0, 11],[0, 1, 4, 5]]
3x+4y+8z = 9
-2x-y = 11
y+4z = 5
400
Solve the System using an augmented equation
4x - y = 19
5x - 5y = 20
(5, 1)
400
Subtract:
[[1,-2, -1],[-3, 4, 3],[5, -6, -5]] - [[-2, 1, 2], [4, 3, -4], [-6, -5, 6]]
[[3,-3,-3],[-7,1,7],[11,-1,-11]]
400
What is AxB?
matrix A=
[[4,3],[9,7]]
matrix B=
[[6,3],[9,4]]
[[51,24],[117,55]]
500
What are the dimensions of
[[1,3, 5,0],[0,1, 6,0],[0,12,1,-5]]
3 x 4
500
Determine the area of a triangle with vertices (-3, 6), (5,2) and (4, -9)
46
500
Solve the following using a matrix equation
5x +2y = 4y+18
- y + 4x = 7 + x
x=-4
y=-19
500
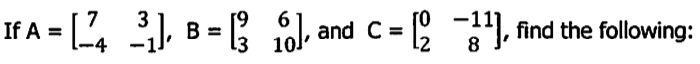2C + A
What is
|7 -19|
|0 15|
500
Solve the following multiplication:
[[1,2, -2, -1],[-3, -4, 4, 3]] xx [[5],[6],[7],[8]]
[[-5],[13]]