solve for y
2x+y=6
y=-2x+6
Add the polynomials:
(x2 +3x + 5) + ( -x2 +6x)
9x + 5
Simplify
(x+5)/(x^2+3x-10)
1/(x-2)
This function has this graph
f(x)=x^2
What are domain and range?
Domain is all the x-values my function can be
Range is all the y-values my function can be
what is i
sqrt(-1)
3(x+2)-8x=x+9
x=-3/6
Subtract the Polynomials:
(k2 + 6k3 -4) - (5k3 + 7k -3k2)
k3 + 4k2 -7k -4
Add:
2/x+3/5
(10+3x)/(5x)
Explain the transformations needed to turn f(x) into g(x)
f(x) = x^2
g(x) = -(x+2)^2 -5
shift left 2 spaces
shift down 5 spaces
reflect across x-axis
Does the table represent a function or just a relation

Relation
what is i2
-1
p2 + -2p - 10 = 5
5, -3
Multiply the Polynomials:
(d + 3)(d2 - 4d + 1)
d3 - d2 -11d + 3
Multiply and simplify:
((x+3)(x+4))/(3x+6)*(x+2)/(x^2+4x)
(x+3)/(3x)
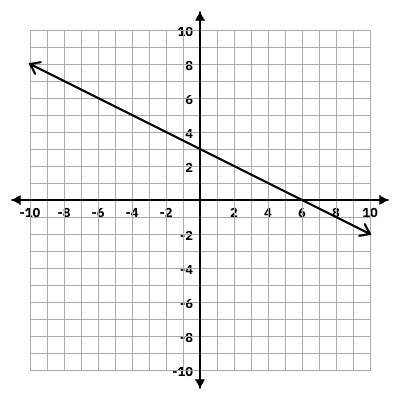
Graph:
y=-1/2x+3
f(x)=x^2-3x+5
Find f(-2)
f(-2) = 15
(5+3i)+(-4-7i)
1-4i
solve
x=sqrt(3x-2)
x = 1, 2
Divide x4-2x3-21x2-10x+22 by x+3.
x^3-5x^2-6x+8-2/(x+3)
Subtract
4/(x+1)-2/(x+2)
(2x+6)/((x+1)(x+2)
Graph:
f(x)=-|x+2|+3
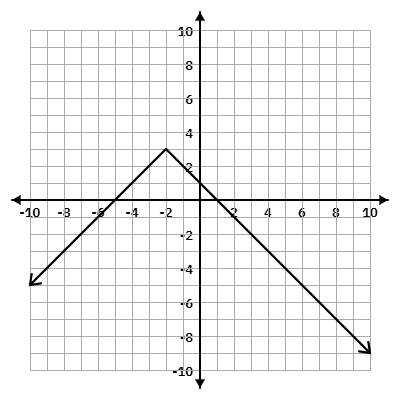
Tell whether the graph is a function or not and then find the domain and range.
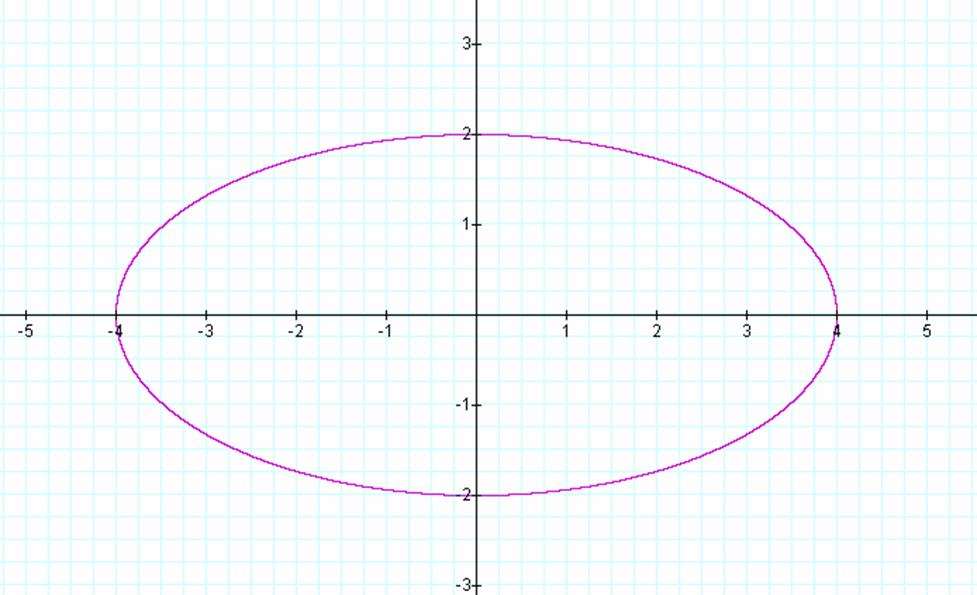
No, Domain: [-4, 4] and Range: [-2, 2]
(-2+5i)-(6+2i)
-8+3i
Solve
\frac{5}{x}+\frac{3x}{x-2}=3
x = 10/11
Divide x3-12x2-42 by x2-2x+1
x-10+(-21x-32)/(x^2 -2x+1)
(x^2+2x-15)/(x^2-4x-45)-:(x^2+x-12)/(x^2-5x-36)
1
Find the linear function that goes through the points (1, 3) and (4, -3)
f(x)=-2x+5
What is the domain of the function in interval notation?
f(x)= x/(x-3)
(-infty,3)uu(3,infty)
(2+4i)(5-2i)
18+16i