Missing Sides
Area and Perimeter
Transformations
Volume
Thinking Problems
100
Mr. Sim’s yard has 4 sides.
• The distance around the yard is 176 feet.
• Three sides of his yard measure 48 feet, 37 feet, and 56 feet.
What is the length of the fourth side?
48+37+56= 141
176-141= 35
100
Area:
Perimeter:
Area: 4 x 5 = 20
Perimeter: 4+5+4+5 = 18
100
You slide your backpack across the floor.
What is Translation?
100
Find the volume of the prism.
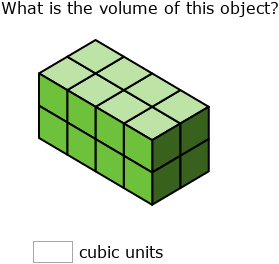
What is 16 cubic units?
100
Ms. Faggard has a teacher desk with a length of 4 feet and width of 2 feet. She wants to know if her new paper holder will fit on her desk. The bottom of her paper holder has a length 1 foot and a width of 2 feet. Will her new paper holder fit on her desk? Why or Why not?
4 x 2= 8 feet
1 x 2= 2 feet
Yes, Ms. Faggards paper holder will fit because the area of the desk is 8 feet and the area of the paper holder is 2 feet. She will have 6 feet left over.
200
Eli has a garden shaped like a triangle with equal length sides. The perimeter of Eli’s garden is 18 feet. What is the length of one side of his garden?
P=18 feet
18/3= 6 feet
200
Some paint spilled on Amina’s rectangle before she could count all the squares. What is the area of Amina’s rectangle? Explain to Amina how you can find the area without counting all the squares.
5 x 3= 15
Amina can find the area of the rectangle by multiplying width times length.
200
The mirror filter on TikTok flips one half of your face onto the other.
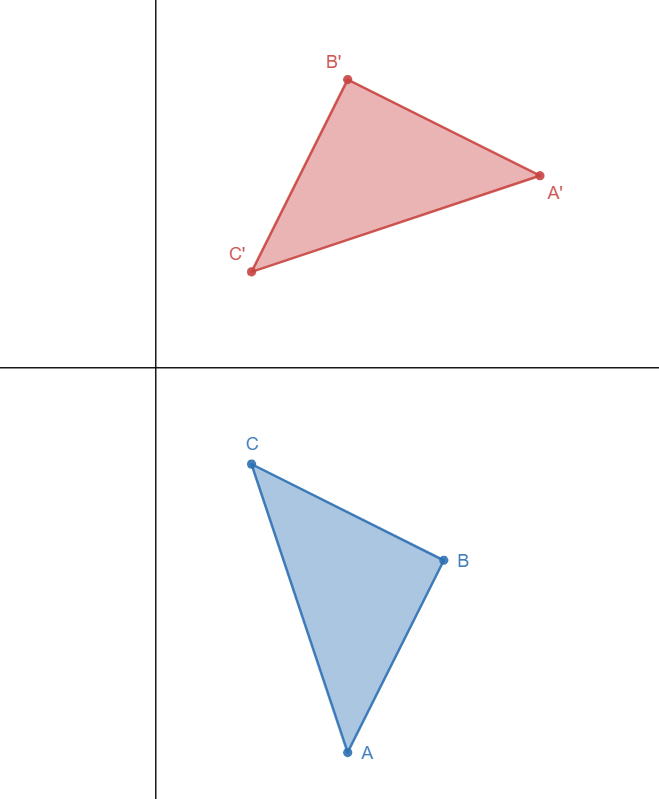
What is a Reflection?
200
Find the volume of the figure.
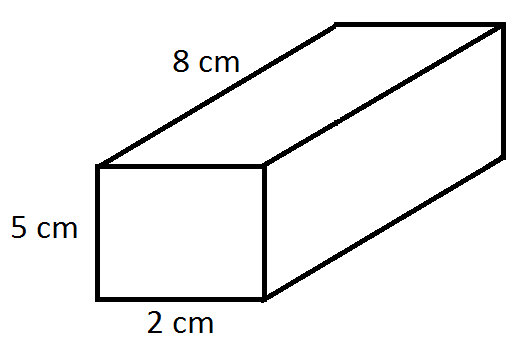
What is 80 centimeters cubed?
200
Rosita is building a chicken coop for her backyard. She needs it to have an area of 45 feet. The length of the coop is 9 feet. What is the width?
45/9= 5 feet
300
Eugene is making a triangular garden. She wants to build a fence around it. She used a total of 76 feet of fencing. 2 of the side lengths were 19 feet and 31 feet. How long is the third side?
19+19+31= 69 feet
76 - 69= 7 feet
300
Michaela ordered a rug for her bedroom. The rug is 7 feet wide and 6 feet long. What is the area of her rug?
7 x 6= 42 feet sq.
300
The picture below shows this type of transformation.
What is rotating?
300
What is the volume of a rectangular prism with measurements of 3 by 5 by 6?
90 cubic units
300
Susan is putting a fence around a new playground. She used 20 feet of fencing. What is one possible drawing of her playground? Include the length and width.
4 x 5= 20
400
Shazir is building a fence around his trapezoidal pasture. He used a total of 98 feet of fencing. Three of the side lengths were 19 feet, 12 feet, and 26 feet. What is the length of the 4th side?
19+12+26= 57
98-57= 41 feet
400
Tyler is putting a fence in his rectangular backyard. His backyard is 45 feet long and 37 feet wide. How many feet of fence will he need?
45+37+45+37= 164 feet
400
The kind of transformation is below...
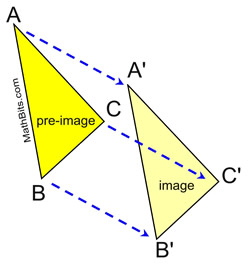
What is a translation?
400
A pencil box has a volume of 100 cubic inches. The length is 10 inches and the width is 2 inches. What is the height?
What is 5 inches?
400
Mia said that Figure Q and Figure R have equal areas and equal perimeters. She supported her thinking by saying that any two figures with the same area always have the same perimeter.
Figure Q: Area= 3 x 4= 12 sq. feet
Figure Q Perimeter = 3+4+3+4= 14 feet
Figure R Area: 2 x 6 = 12 sq. feet
Figure R Perimeter: 2+6+2+6= 16 feet
500
48/6= 8 feet
28-12=16 inches
500
A video game map has a total area of 18 square inches. What are possible dimensions of the map?
There are 2 answers for this question.
9 x 2= 18
3 x 6= 18
500
You are walking to the bus stop, then realize you forgot your math homework. You turn around, then walk back home to pick it up.
What is Rotation, then translation?
500
A box has a length of 12 centimeters, a width of 10 centimeters, and a height of 6 centimeters. A second box has a length of 60 centimeters and a width of 2 centimeters. Both boxes have the same volume. What is the height of the second box?
What is 6 centimeters?
500
The dimensions of a garden shed are shown below. Circle the equation that correctly identifies how to decompose this figure to find the total area.
A. (2 x 2) + (3 x 3) = 10 sq. cm
B. (5 x 2) + (5 x 3 )= 25 sq. cm
C. (3 x 3 ) + (2 x 5) = 19 sq. cm
D. (3 X 2) + ( 5 x 5)= 31 sq. cm
(2x5)+(3x3)=
10+9= 19
Answer choice C