Change in Arithmetic and Geometric Equations
Mixed
Exponential Equation from 2 points
Solving Exponential Equations
Composition of Functions
100
an= 2(4)n
Find a2
32
100
Samuel. M collects lizards to sell them as pets. He collects more lizards after it rains. The number of lizards he collects during the day is best fit to the line y= -x2+4x+15, where x is the number of days since it last rained. If Samuel collects 14 lizards 5 days after it rains, what is the residual value for that data point?
The residual value is 4.
100
Find the exponential equation f(x) from the following points.
(0,3) & (1,1)
f(x)= 3(1/3)x
100
91= 7(2)x
Solve for x and round to the nearest hundredth.
x=3.7
100
f(x)=5x
g(x)=3x3
Find f(g(2))
f(g(2))=120
200
Identify if the following series of numbers is an arithmetic sequence, geometric sequence, or neither and why.
1,2,3,5,8,13,21,34,65....
Neither, the sequence does not follow any set difference or set ratio.
200
Prayas bought a gaming computer for $8,100. He then spent $2000 dollars on candy bars and then spent $250 on RGB lights on his room. After 3 years, his computer depreciated to $5000. The price of his computer over time can be modeled by the function y= 8100(0.851455)x
How much money did Prayas spend in total on just his computer alone when he first bought it?
$8100
200
What are two points that could be used to determine the exponential function f(x)= 7(2)x?
Answers will vary
Ex. (0,7) & (3,56) or (1,14) & (4,112)
200
In 2018, RJ bought a share of FC Barcelona's stock for $50. The value of the stock increases by 5.7% per year. How much is RJ's stock worth in 2025?
Round to the nearest cent*
$73.70
200
f(x)=3x-1
g(x)=x/3
Find f(g(x)) and g(f(x)) and determine if they are inverses
f(g(x))= x-1
g(f(x))=x-1/3
NOT inverses
300
a34=224 d=5
Write an explicit formula for the series and find a59.
an= 54+5n
a59=349
300
The number of calories that Trevor burns at the gym is best fit to the linear function y=214.54x+23.12, where x is the number of hours spent at the gym. If Trevor burns 660 calories after 3 hours at the gym, what is the residual squared value for that data point?
45.43
300
Find the function f(x) from the following points:
(2,4) & (4, 36)
f(x)= 4/9(3)x
or
f(x)=4/3(3)x-1
300
RJ bought a car for $74,000. The car began to depreciate at a rate of 6% every day. How much is RJ's car worth after 14 days?
Round to the nearest cent*
$31,118.72
300
f(x)= √2x
g(x)= x+4
h(x) is defined as being f(g(x)). Find h(x) and state its domain.
h(x)=√2x+8
Domain (-4, ∞)
400
Two values of a geometric sequence are given
a-1=2
a1=50
Find a8
3906250
400
Mr.Hoke launches a rocket to Jupiter and its speed increases at an exponential rate. The initial speed of the rocket when it takes off is 480 mph and the speed of the rocket 37 hours after it takes off is 2000 mph. What is an exponential equation that could model this scenario and how fast was the rocket going 12 hours after it took off?
Round to the nearest thousandth on all values*
y=480(1.039)x
Mr Hoke's rocket was going 762.487 mph after 12 hours.
400
Find the function f(x) from the following two points:
(2,5), (8,3645)
f(x)=5/9(3)x
400
Juan bought a carpet from a furniture store which had a value of $2,500. Every day, Ryan's cat scratches the carpet, causing it to depreciate in value by 12.3% per day. What percentage of value does Juan's carpet lose per week?
Round to the nearest tenth percent*
60.1%
400
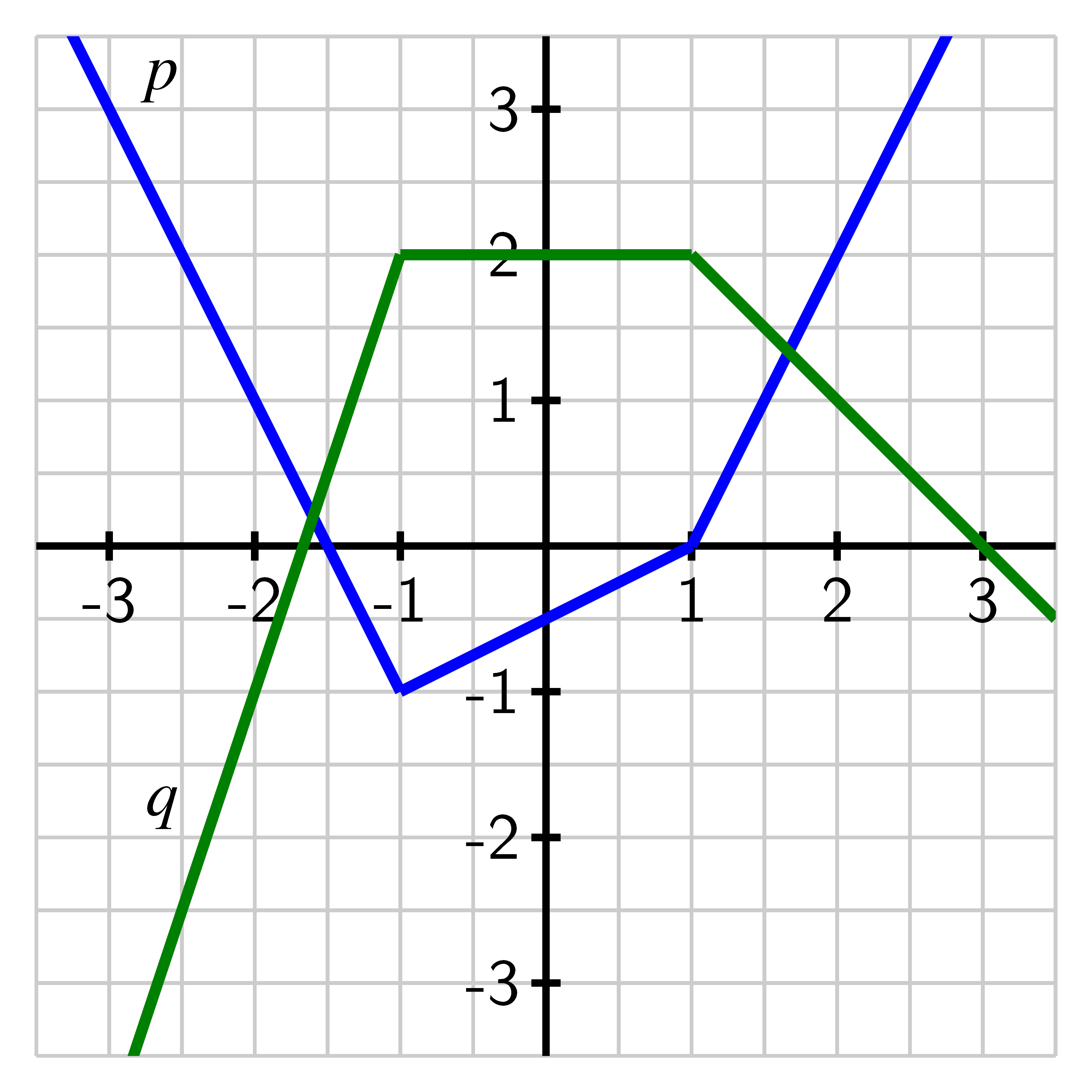
The graph above shows the functions p and q over a domain. Find p(q(p(2)))
p(q(p(2)))=0
500
How many terms are in the arithmetic sequence?
{3,7,11....127}
32 Terms
500
Find the exponential equation from the table below in the form a(b)x+c. 
y=-1.5(0.5)x+4
500
Find the function f(x) from the following two points.
(2, -4) & (4, -36)
f(x)=-4/9(3)x
500
A culture of bacteria grow at an exponential rate. After two hours, the culture is at a population of 2560 bacteria. After 5 hours, the population is at (approximately) 10485.76 bacteria. How many bacteria will be in the culture after 12 hours, to the nearest whole number?
281475 bacteria
500
f(x)= 1/5x2
g(x)= 5x-2
Find f(g(x))
f(g(x))=x4/125