Solving
Slope
Word Problems
Polynomials
Misc.
100
Solve the following: -4x + 8 = 24
x = -4
100
Find the slope of the line that passes through the points (2, -1) and (3,4)?
m = 5 or m = 5/1
100
Marc is having a bake sale. He sells 14 cupcakes and 26 cookies. He makes a total of $150. What are the variables in the following situation?
x = cost of cupcakes
y = cost of cookies
100
Simplify the following:
(2x2 + 5x - 9) + (x2 - 2x - 11)
3x2 + 3x - 20
100
What type of function is this?
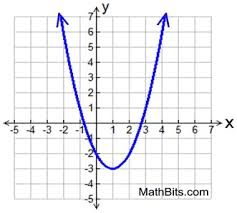
Quadratic
200
Convert to slope-intercept form:
6x - 3y = 12
y = -4 + 2x
or
y = 2x - 4
200
Find the slope of the line that passes through the points (0,8) and (-1,10)?
m = -2 / 1 or m = -2
200
You have saved $20 toward buying a new computer game. Each week you save $5 more. Define variables and create an equation to model this situation.
x = # of weeks
y = total amount saved
y = 5x + 20
200
Simplify the following:
(4x2 - 8x + 10) - (2x2 - x)
2x2 - 7x + 10
200
How many solutions does the following have?
3x - 9 = -9 + 3x
Infinite Solutions
300
Solve the following:
-3x - 6 > 9
x < -5
300
What is the slope and y-intercept of the following?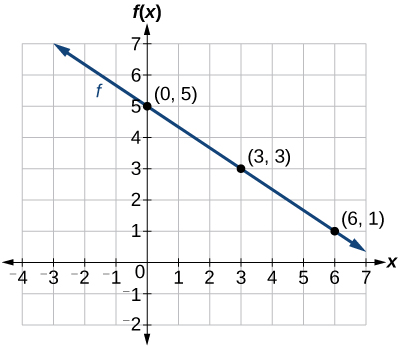 
y-intercept: (0, 5)
Slope: -2/3
300
Bowser is trying to lose weight. He weighs 170 pounds, and he plans on losing 5 pounds each month. How much will he weigh after 4 months?
He will weigh 150 pounds
300
Simplify the following:
2(-2x2 + 6x - 1) - (6x2 + 4x - 12)
-10x2 + 8x + 10
300
Simplify the following:
50 + 8
9
400
Solve the following system of equations:
x = 4y
2x - 6y = 12
(24, 6)
400
What is the slope and y-intercept of the following?
y-intercept: (0, -3)
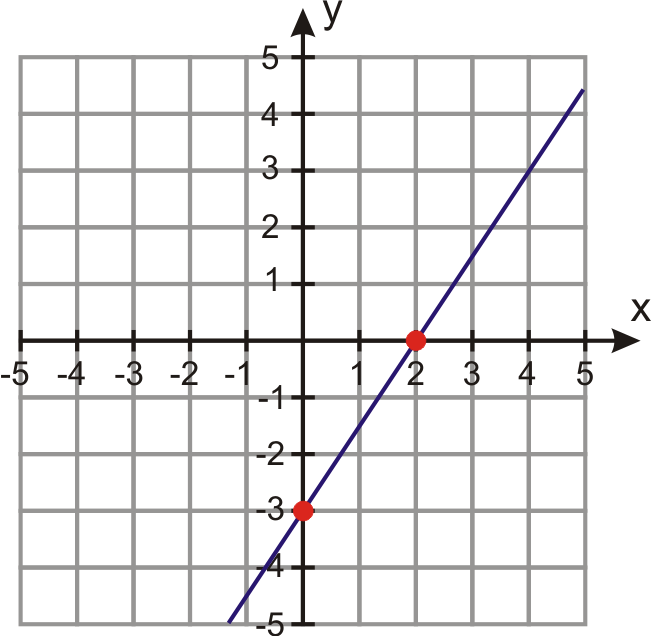
slope: 3/2
400
Name all five Freshman Academy math teachers
Ms. Henzer
Ms. Hirsch
Ms. Jackson
Mr. Landzberg
Ms. McGreal
400
Simplify the following:
(2x - 4)(x - 6)
2x2 - 16x + 24
400
y < 4x - 3
Identify the following:
Slope? Dashed/solid?
Y-intercept? Above/Below?
Slope: 4 or 4/1
Y-intercept: (0, -3)
Dashed
Below
500
Solve the following system of equations:
2x + 3y = 15
x - 3y = 3
(6, 1)
500
Find the solution of the following system of equations:
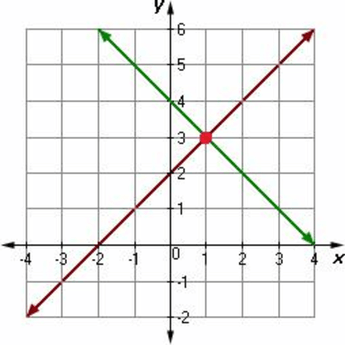
(1, 3)
500
Boxes of candy canes cost $4 and gingerbread cookies costs $2. You spend exactly $40 on boxes of candy canes and gingerbread cookies. Define your variables and write an equation to model this situation.
If you bought 2 gingerbread cookies, how many boxes of candy canes did you buy?
x = # of boxes of candy canes
y = # of ginger break cookies
4x + 2y = 40
You bought 9 boxes of candy canes
500
Simplify the following:
(6x2 + 8x - 2)(2x - 3)
12x3 - 2x2 - 28x + 6
500
Solve the following: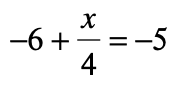 
x = 4