Solving Equations
Inequalities
Absolute Value
Linear Functions
Linear Functions
100
-66 = -9n + 16n + 4
n = -10
100
h - 4.7 > -1.2
h > 3.5
100
l 9z - 8 l = 3
z= 11/9, z=5/9
100
Write an equation of the line that passes through points (3, 1) and (0, 10)
y = −3x + 10
100
Determine whether the relation is a function.
(1, -2), (2, 1), (3, 6), (4, 13), (5, 22)
Yes, it is a function
200
3( -5y + 2) = 21
y = -1
200
-8 ≤ (2/3) w
w ≥ -12
200
l -5y + 9 l = 2y
y= 9/7, y= 3
200
Write a linear function with the given values: f(0) = 2 and f(2) = 4
f(x) = x + 2
200
What is the domain and range?
.png?revision=1)
domain: all real numbers
range: y ≥ -9
300
5x - 1 = 7x + 5
x = -3
300
13 - n + 2n > 8 + 1
n > -4
300
2 + l x + 4 l = 7
x=1, x= -9
300
Find the x and y intercepts of the line: y = 3x + 9
y intercept: (0, 9)
x intercept: (-3, 0)
300
Tell whether the graph shows a positive, negative or no correlation.
negative correlation
400
2(1 - 8x) = 1/4(8 - 64x)
x = 0
400
3(4x + 10) ≥ 3(2x - 6)
x ≥ -8
400
12 - 4 l 2d + 18 l = 4
d= -8, d= -10
400
Write an equation in slope-intercept form that passes through the given points: (7, 2) and (2, 12)
y = −2x + 16
400
Write an equation of the line.
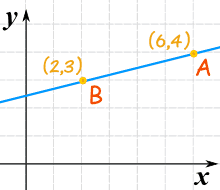
y = 1/4x - 5/2
500
8(5z - 7) = -4(-10z+14)
infinitely many solutions
500
8(3g - 2) ≤ 12(2g +1)
no solution
500
In a speech class, students must give a final speech for their exam. The speech can be 15 minutes, or within that time by 4 minutes. Write an absolute value equation that represents the minimum and maximum lengths of the final speech.
l t - 15 l = 4
500
Determine which lines are parallel.
Line a passes through (−1, −2) and (1, 0).
Line b passes through (4, 2) and (2, −2).
Line c passes through (0, 2) and (−1, 1).
Lines a and c are parallel
500
In 1960, the world record for the men's mile was 3.91 minutes. In 1980, the record time was 3.81 minutes. Write a linear model that represents the world record (in minutes) for the men's mile as a function of the number of years since 1960.
y = −0.005t + 3.91