Exponential Growth and Decay
Compound Interest
Exponential and Log Model
100
Sophie invested $5,000 into an account that will increase in value by 2.3% each year. Write a function to model this situation, then find the value of the investment after 15 years.
f(t)=5000(1+0.023)^t
f(t)=5000(1.023)^t
f(15)=5000(1.023)^15
$7,032.42
100
A realtor took $32,500 made on the sale of a home and placed it in a new account that earns 6% compounded annually. Find the total amount in the account after 5 years.
f(t)=32500(1+0.06/1)^(1t)
f(5)=32500(1+0.06/1)^(1*5)
$43,492.33
200
A baseball card that was valued at $200 in 1980 has increased in value by 7% each year. Write a function to model this situation, then find the value of the card in 2016.
f(t)=200(1+0.07)^t
f(t)=200(1.07)^t
f(36)=200(1.07)^36
$2,284.79
200
Miles invested $2,400 into a retirement account that earns 1.8% interest compounded bimonthly. Write a function to model this situation, then find the balance of the account after 25 years.
f(t)=2400(1+0.018/24)^(24t)
f(25)=2400(1+0.018/24)^(24*25)
$3,763.31
200
The table below shows the value of a stock over the course of five years. Using an exponential model, write an equation for the curve of best fit, then estimate the value of the stock in 2025.
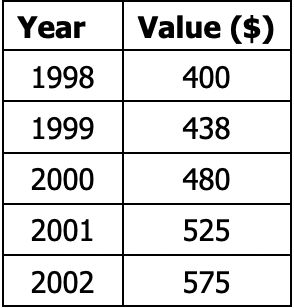
f(x)=400.07*1.09^x
f(27)=400.07*1.09^27
$4098.75
300
A virus has infected 400 people in the town and is spreading to 25% more people each day. Write an exponential function to model this situation, then find the number of people that will be infected in 10 days.
f(t)=400(1+0.25)^t
f(t)=400(1.25)^t
f(10)=400(1.25)^10
f(10)=3725.29
3725 people
300
Sarah moved $30,000 of her savings to a new investment account that earns 4% interest compounded quarterly. Write a function to model this situation, then find the amount of interest the account will earn after 12 years.
f(t)=30000(1+0.04/4)^(4t)
f(12)=30000(1+0.04/4)^(4*12)
$48,366.78
Interest:
$48,366.78-$30,000=$18,366.78
300
The table below shows the wind speed along with the corresponding wind chill factor. Using a logarithmic model, write an equation for the curve of best fit, then find the approximate wind speed that corresponds to a wind chill factor of -18 °F.
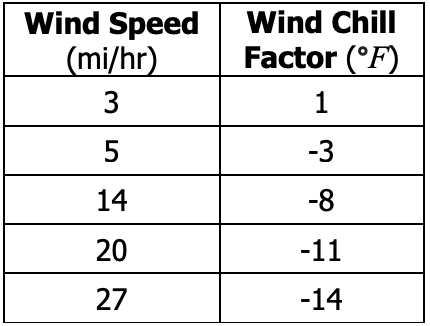
f(x)=7.91-6.41*ln(x)
-18=7.91-6.41*ln(x)
-25.91=-6.41*ln(x)
ln(x)=4.04
e^4.04=x
x=56.95
57 mph
400
The population of a small town was 10,800 in 2002. Since then, the population has decreased at a rate of 2.5% each year. Write an exponential function to model the situation, then find the population of the town in 2020.
f(t)=10800(1-0.025)^t
f(t)=10800(0.975)^t
f(18)=10800(0.975)^18
f(18)=6847.10
6847 people
400
Scott invested $1,600 into a retirement account that earns 2.4% interest compounded monthly. What will the balance of the account be after 30 years?
f(t)=1600(1+0.024/12)^(12t)
f(30)=1600(1+0.024/12)^(12*30)
$3,284.73
400
The table below shows the number of students enrolled at Glennview High School during certain
years. Using an exponential model, write an equation for the curve of best fit, then estimate
the year in which enrollment reaches 2,000 students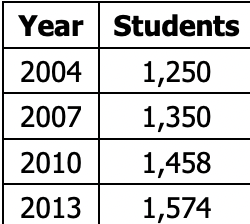
.
f(x)=1250.10*1.03^x
2000=1250.10*1.03^x
1.03^x=1.5999
log_1.03(1.5999)=x
log1.5999/log1.03=x
x=15.8985
2004+15.8985=
2019
500
Manny bought a brand new car in 2012 for $28,750. If the car depreciates by 12% each year, write an exponential function to model the situation, then find the value of the car in 2018.
f(t)=28750(1-0.12)^t
f(t)=28750(0.88)^t
f(t)=28750(0.88)^6
f(6)=$13351.62
500
Kaylee used her graduation money to set up a savings account that earns 3.4% interest compounded weekly. If the original amount deposited was $500, how much interest will she have earned after 10 years?
f(t)=500(1+0.034/52)^(52t)
f(10)=500(1+0.034/52)^(52*10)
$702.40
Interest:
$702.40-$500=$202.40
500
The table below shows the weights of five females of the same height along with their body mass
index, BMI. Using a logarithmic model, write an equation for the curve of best fit, then
estimate the BMI of a female that weighs 130 pounds.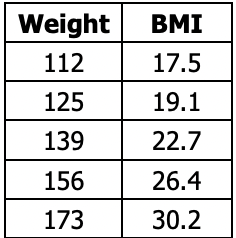
f(x)=-124.72+29.96lnx
f(130)=-124.72+29.96ln(130)
21.11