These transformations take f(x)=x3 onto g(x)=x3 - 4.
What is a vertical shift of four units down?
A student says the degree of 3x2+4x+7 is 7.
What's the mistake?
The student confused the constant with the degree. The correct degree is 2.
What are the zeros and their multiplicities of the graph?
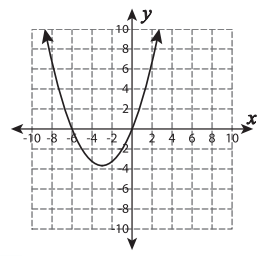
0 multi 1
-6 multi 1
How many relative extremas does the graph have? 
4
Name the polynomial:
7x+2
linear binomial
This kind of function is built by multiplying linear factors to make higher-exponent x terms, such as f(x)=3x2+7x-1, g(x)=-2x3-2x2+x+1, or h(x)=(x+1)(x-2)(2x+3)(x-5).
Polynomial
These transformations take f(x)=x2 onto g(x)=(x-5)2.
What is a horizontal shift of five units to the right?
A student identifies the leading coefficient of -7x4+3x2-2 as -2.
What is the mistake?
-2 is the constant term. The leading coefficient is -7.
Identify the zeros and their multiplicities of the graph
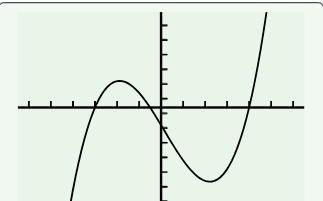
-3 multi 1
-0.5 multi 1
-4 multi 1
How long did it take Karen to run a marathon?
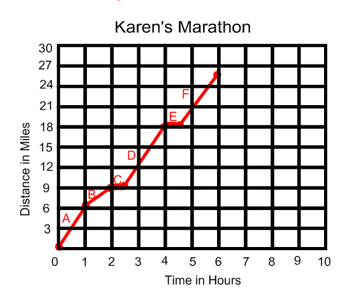
6 hours
Name the polynomial:
5x3
Cubic Monomial
The highest exponent in a polynomial function.
Degree
These transformations take f(x)=x2 onto g(x)=3(x+1)2 - 2.
What is a horizontal shift of one unit left, a vertical shift of two units down, and a vertical dilation by a factor of three (making the graph skinny)?
A student states that the degree of the binomial 4a3b2c+ab2 is 5.
What is the mistake?
The student forgot to include the exponent of 1 for the variable c when adding the exponents. The correct degree of the binomial is 6.
Identify the zeros and their multiplicities of the function
f(x)=x^2(x-1)^2(x+3)
0 multi of 2
1 multi 2
-3 multi 1
What was the highest point the diver made it?
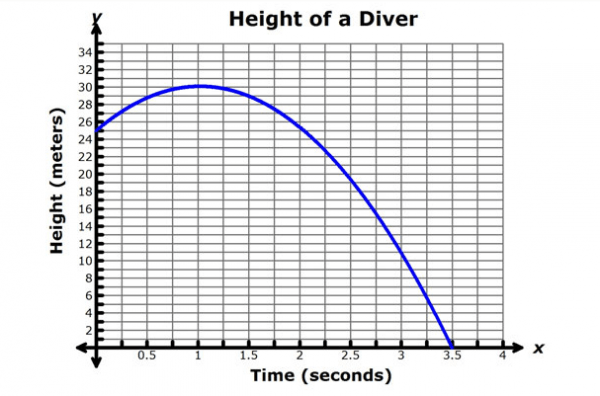
30 meters
Name the polynomial:
m5n2+mn2+n
quintic trinomial
In a polynomial, this number is multiplied by the power of x that determines the function's degree.
leading coefficient
Write the new equation of f(x)=x3 given the following transformations:
1. a vertical shift of four units down
2. a horizontal shift of one unit left
3. a vertical compression by a factor of 1/3
4. a reflection over the x-axis?
f(x) = -(1/3)(x+1) - 4.
The student writes that 4x3-2x+5x3 is a trinomial.
What's the mistake?
Like terms were not combined. It's a binomial: 9x3-2x
Identify the zeros and their multiplicities. Then determine the degree of the function.
f(x)=-x(x+7)^3(x+2)^2
o multi 1
-7 multi 3
-2 multi 2
6th degree
How long did it take the diver to hit the water?
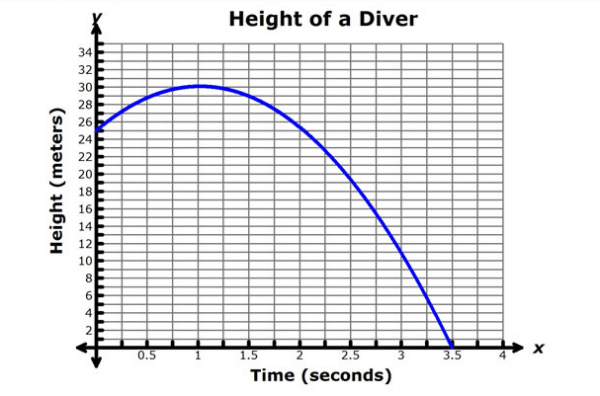
3.5 seconds
Name the polynomial:
2a3b+9a2bc2
Cubic Binomial
a single number, a variable, or a product of numbers and variables, separated by addition (+) or subtraction (-) signs in an expression, acting as the building blocks of equations
term
Write the new equation of f(x)=x3 given the following transformations:
1. a horizontal shift of four units left
2. a vertical shift of one unit up
3. a vertical compression by a factor of 1/2
3. a reflection over the x-axis (making it open down).
f(x)=-1/2(x+4)3+1
A student says that the expression x2+3x+1 is a monomial because it's just one variable.
What's the mistake?
It has three terms, not one. It's a trinomial, even though there is only one variable.
Identify the zeros and their multiplicities. Then determine the degree of the function.
f(x)=x^2(x-5)^5(x+1)^2(x+4)
0 multi 2
5 multi 5
-1 multi 2
-4 multi 1
10th degree
Which thrower threw the furthest? 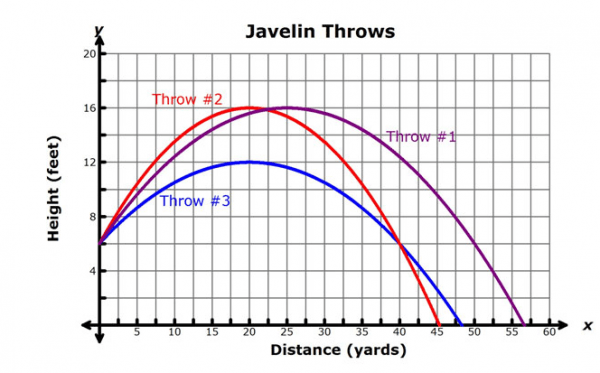
#1
What is the correct name for:
x4+2x3+x2+x+1
Quartic Polynomial
a function that moves, flips, or resizes a shape or graph, changing its position, orientation, or size
transformation