Direct & Inverse
Rationals & Radicals
Square Root Functions
Graphs
Word Problems
100
Does this equation represent direct variation, inverse variation, or neither:
xy = 3
Inverse!
100
When converting between rational and radical form, you should remember ________ over _______!
Power over root
100
What would the first step be in solving this equation?
Subtract 1 from both sides
100
What are the intercepts for the original square root function?
(x and y intercepts)
(0,0)
100
Jim's wages vary directly with the number of hours he works. Last week he got paid $27 for 5 hours of work. How much will he get paid for 30 hours of work?
$162
200
Does the following represent direct variation, inverse variation, or neither:
Direct!
200
In radical form, if no exponent is shown, you assume the power is _______, if there is no root shown, you assume the root is _________.
1,2
200
Solve for x:
x = 64
200
What is the domain and range for the original square root function?
D: x > 0, y > 0
200
The number of kilograms of water in a person's body varies directly with the person's mass. A person with a mass of 90 kg contains 60 kg of water. How many kilograms of water are in a person with a mass of 50k g?
33.3 kg
300
Given that y varies directly with x and y = -4 when x = 2, find y when x = -6.
y = 12
300
Write in radical form:
(6x)3/4
Fourth root of (6x)3
300
Solve the following for x:
x = 1/3
300
Write the equation for this graph:
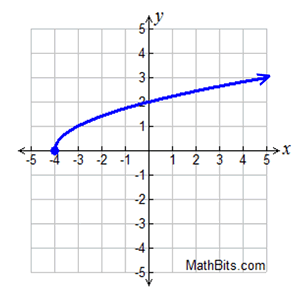
sqrt(x+4)
300
The time it takes to fly from Los Angeles to New York varies inversely as the speed of the plane. If the trip takes 6 hours at 900 km/h, how long would it take at 800 km/h?
6.75 hours or 6 hours, 45 min
400
If x varies inverse as y, and x = 7 when y = 3, find y when x = 9.
21/9 , 7/3, or 2.3333
400
Write in rational form:
x5/4
400
Solve the following:
√(2x+9) − 5 = 0
x = 8
400
Write the equation for the following graph:
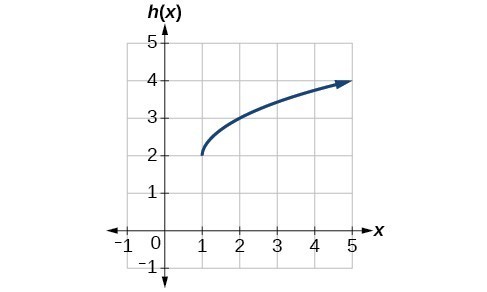
y = sqrt(x-1) + 2
400
On a string instrument, the square of the length of a string varies inversely as the frequency of its vibrations. A 10 inch string has a frequency of 400 cycles per second. Find the constant of proportionality.
40,000
500
If a varies inversely as square root of b, and a = 7 when b = 36, find a when b = 289.
42/17 or 2.47
500
Conver to radical form:
6x-4/2
1/ sqrt(6x4)
500
Solve for x:
x = -6, x = -1
500
State the domain and range for this graph:
D: (1, infinity) R: (2, infinity)
500
On a string instrument, the square of the length of a string varies inversely as the frequency of its vibrations. A 10 inch string has a frequency of 400 cycles per second. Find the frequency of a 15 inch string.
177.8 cycles per second