1. Define Acceleration. What is its SI unit?
Velocity / Time
m / s2
2. Draw the velocity-time graph for free fall
Refer graph
3. When a ball is thrown upward, what are the velocity and acceleration at the highest position?
acceleration = - g
velocity = 0
4. A body falling from rest. The ratio of distance travelled by the body in equal intervals, according to Galileo is _________
1: 3 : 5 : 7 :
5. Which of the following statement is Correct?
a)The magnitude of the displacement is always less than or equal to the distance.
b)The magnitude of the displacement is always greater than or equal to the distance.
Displacement is the shortest distance.
So statement a) is correct.
6. Distinguish between speed and velocity.
Speed - Distance /Time, Scalar quantity
Velocity - Displacement / Time. Vector quantity
7. Draw a velocity-time graph for uniform motion
In uniform motion, velocity is a constant.
So the graph is a straight line parallel to the time axis.
8. Slope of velocity time graph gives ______________
Area of velocity time graph gives _____________
Acceleration
Displacement
9. When does the average velocity becomes equal to the instantaneous velocity?
When delta t tends to zero
or for uniform motion
10. The speedometer of the bus measures ______________
Instantaneous speed
11. A car covers the first half of the distance between 2 places at a speed of 40 km/h and the second half at 60 km /h. Calculate the average speed of the car.
2 v1 v2 / ( v1+ v2) = 2 x 40 x 60 / (40 +60) = 48 km /h
12.An aeroplane travels travels 280 m through the running before taking off. It starts from rest,moves with constant acceleration and takes off after 8s. What is its speed when it takes off?
x = at2 / 2
280 = a x 82 / 2 , a = 35 / 4
v = at =35 /4 x 8 = 70 m/s
13. A car travels from A to B at 60 km /h and returns to A at 90 km/h. Find the average velocity and average speed in km /h
Avg velocity = Displacement / Time = 0
Avg speed = Distance /Time = 2d /(d/s1 + d /s2)
= 2 s1 s2 /(s1 + s2) = 2 x 60 x 90 / (60 + 90)
= 72 km /h
14. Starting from rest, a car moves with uniform acceleration and attains a velocity of 10m/s in 10s. It then moves with uniform speed for 15s and is then brought to rest in 12s under uniform retardation. Draw a velocity-time graph and find the total distance covered.
Refer graph
Total distance = 10x10/2 + 15x10 + 10x12/2 = 260m
15. Find the distance and displacement in the following case.
P-----------x----------------R-------------x----------------Q
P to Q then back to R
Distance = PQ + QR = 3x
Displacement = RP = x
16 .Draw a) a velocity-time graph and b) a speed-time graph of a stone thrown vertically upwards and comes back
Refer graph
17.Velocity- time graph of a body is given below.
a)Which portion of the graph represents uniform retardation?1)OA, 2)AB, 3)BC, 4)OC
b)Find the displacement in time 2s to 7s
a)BC
b)Displacement = 5x6/2 = 30m
18.Derive the relation v = u + at
By definition, a = ( V2 - V1) / (t2 - t1)
Put V1 = u , V2 = v , t1 = 0 , t2 = t
So a = v - u / t or at = v - u
or v = u + at
19. Acceleration -time graph of a body starting from rest is as shown in the figure. Draw the velocity-time graph . Also, find the displacement in 0 to 3 seconds.
Refer the graph
S = 3x12/2 = 18 m
20. The velocities of two bodies A and B are given in the tables. From this table, find which body is moving with uniform acceleration. Explain.
Body A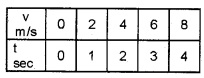
Body B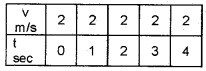
Body A is moving with uniform acceleration because the velocity of the body increases at the rate of 2 m/s2.
Body B is moving with constant velocity. Hence this motion is called uniform motion.
21. Derive the position-velocity relation for uniformly accelerated motion.
x = ut + at2 / 2 = ut + (v - u) t 2 / 2t
x = ut + vt / 2 - ut / 2 = (v + u )t / 2
x = (v +u ) (v - u ) /2a or 2ax = v2 - u 2
22.2 balls are thrown simultaneously. A vertically upwards with a speed of 20m/s from the ground and B vertically downward from a height of 40m with the same speed along the same line of motion. At what point do the 2 balls collide? Take g = 9.8 m /s2
For A , u 20 m/s, g = - 9.8 m/s2
x =20t -4.9 t2 ---------(1)
For B,u = - 20 m/s , g = - 9.8 m/ s2
- (40 - x) = - 20t -4.9 t2 or 40 - x = 20t + 4.9 t2 --------(2)
(1) + (2) = 40 = 40t So t = 1 sec, x = 20 - 4.9 =15.1m
23. Derive the relation x = ut + at2 / 2 using velocity-time graph for uniformly accelerated motion.
Refer graph
Area = x = ut +( v - u ) t / 2 = ut + at t /2
x = ut + at2 / 2
24. The position-time graph of two bodies A and B (at different situations) are given in the following graphs. Find the relative velocities of the following graph.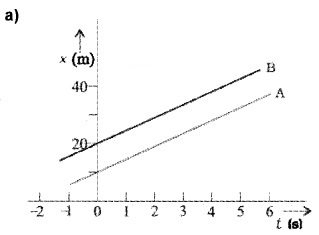
The slope of A and B are equal. Hence velocity of A and B are equal. So velocity of A with respect to B, VAB = 0
25. The position-time graph of a body moving along a straight line is shown below. Draw the velocity-time graph of the body from the position-time graph. Also, find the displacement in 20 s.
v = (x2 - x1 ) / (t2 - t1)
v = (10 - 0) / (5 - 0)=2
v = (10 - 10) / (15 - 5) = 0
v = (0 -10) / (20 -15) = -2
Displacement in 20 sec = 0