This is what happens when a shape is dilated
it gets bigger or smaller.
This is an example of translating.
moves positions without while looking exactly the same.
The measurement that describes rotating
degrees
This is what happens to a shape when reflecting
it flips
This is how you show translating up 6 units without a graph
(x, y+6)
The graph depicts a rigid transformation. What is the rule? Give the words and the notation.
1 unit right 2 units down: (x + 1, y - 2)
This is the dilation that happens when an ordered pair changes from (2,3) to (4,6)
dilation by a factor of 2
Adding to the x-coordinate moves a figure in these directions.
to the right
When both coordinates change signs but do not switch this is the rotation.
180 degree rotation
This coordinate stays the same when a figure is reflected across the y-axis.
the y-coordinate.
Describe this transformation rule: (x + 8, y - 3)
translate 8 units right and 3 units down
The given graph depicts a rigid transformation.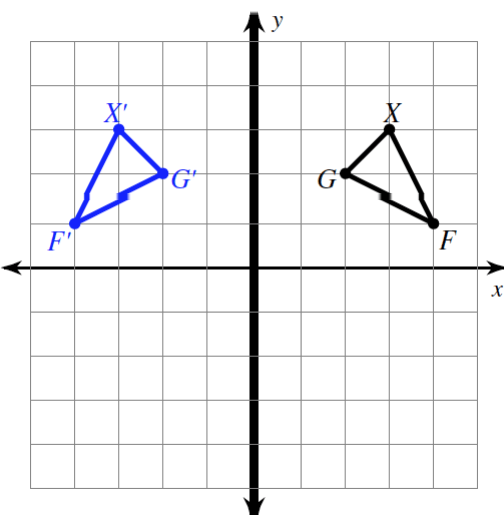
a reflection in the y-axis
The given graph depicts multiple transformations of the pre-image *. This image depicts a dilation of *.
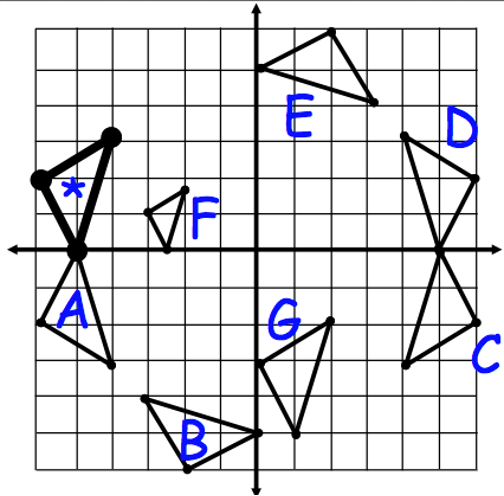
figure F
If (1, 6) is translated to the left 3 and down 1, what are the new coordinates?
(-2, 5)
The segment below has been rotated 90o in what direction?
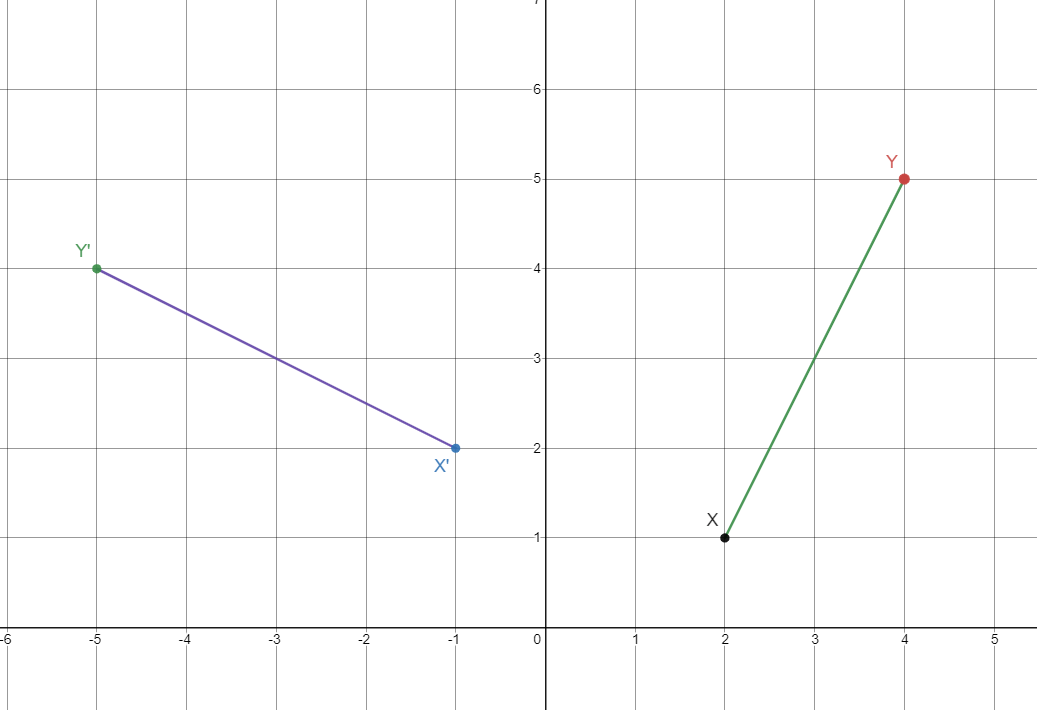
counterclockwise
This coordinate changes when a figure is reflected across the y-axis.
the x-coordinate
If (1,5) becomes (3,0) what is the transformation rule?
(x + 2, y - 5)
The given graph depicts multiple transformations of the pre-image *. This image depicts a Reflection of * across the y-axis.
shape D
The answer to this problem (without a graph).
J(−4, 4), K(−3, 4), L(−1, 1), M(−4, 1)
Dilation by a factor of 3, and then 180° rotation about the origin
J(12, -12), K(9, -12), L(3, -3), M(12, -3)
This is what happens to the coordinates if a figure translates up and to the left.
subtract from the x-coordinate and add to the y-coordinate?
This is the coordinate M' after the figure below is rotated 180o clockwise.
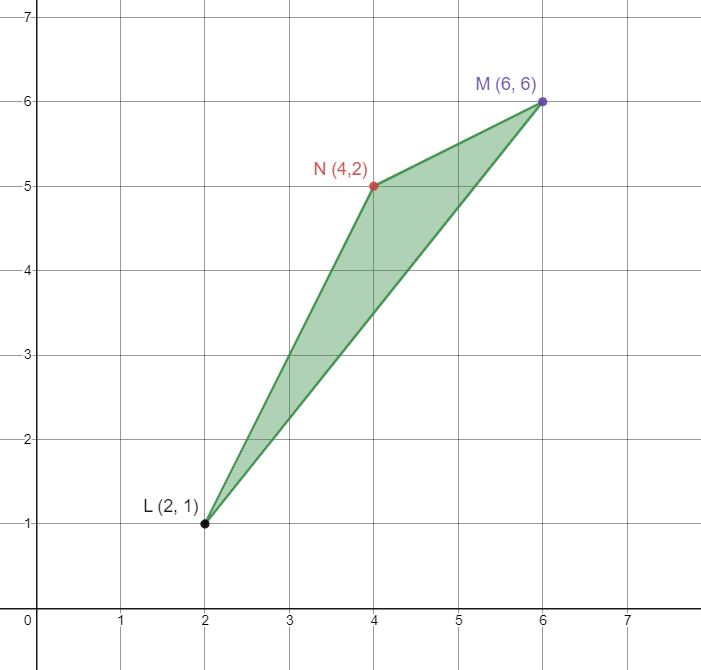
(-6, -6)?
The figure has been reflected over this line.

the x-axis
The answer to this problem (without a graph).
R(−7 ,−5), S(−1, −2), T(−1, −5)
Rotate 90° counterclockwise about the origin. Then translate 3 units left and 8 units up
R(2, 1), S(-1, 7), T (2, 7)
The given graph depicts a rigid transformation.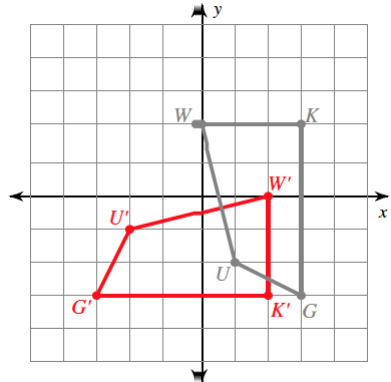
90-degree clockwise or 270-degree counterclockwise rotation
What is the transformation that happens between a boys basketball and a girls basketball.
Dilation
With the green figure being the original. The translation for the figure below.
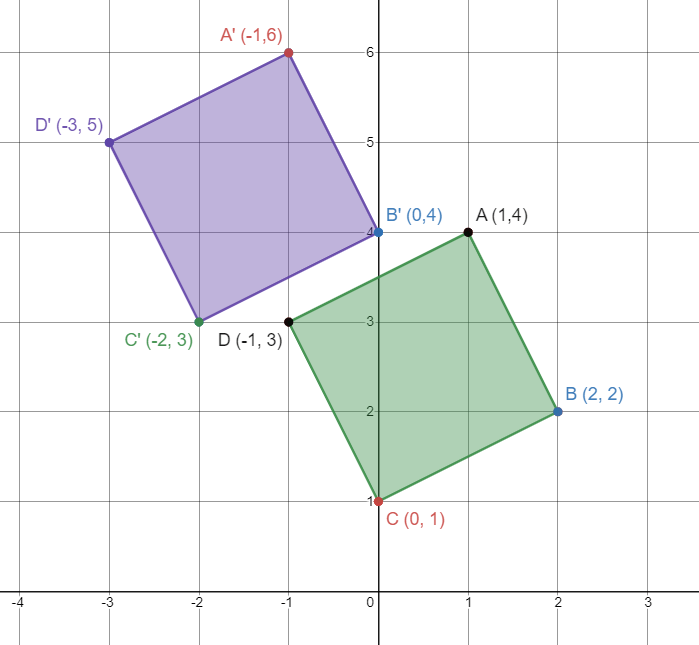
left two units, up two units
This clockwise rotation is the same as rotating 90o counterclockwise.
270o clockwise
Reflect the triangle ABC over y-axis with side lengths AB =3 units, BC = 4 units and AC = 5 Units. This is the length of side BC after the reflection
4 Units.
Name the four types of Transformations.
Translation, reflections, rotations, dilations
The given graph shows rigid transformations of the pre-image . Triangle * will have a Rotations of 90-degrees counterclockwise about the origin. Where will the new figure be? 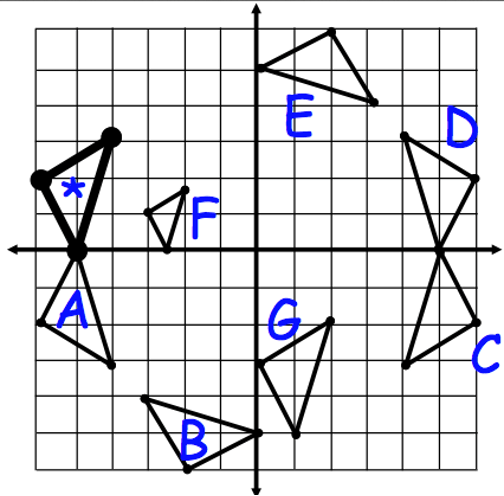
figure B