Unit Circle
Six Trig Functions
Trigonometric Identities
Right Triangles
SPT Trivia
100
Draw the first quadrant of the unit circle.
100
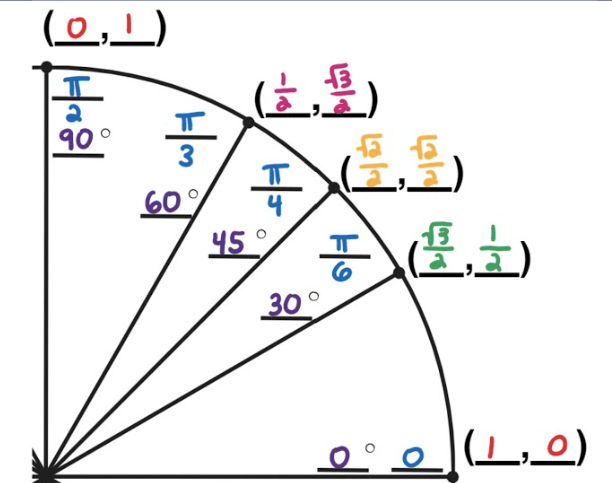
Determine the quadrant where cosθ>0 and tanθ<0.
Quadrant IV
100
Categorize sinx, cosx, tanx, cotx, cscx, secx as even or odd.
Even: cosx, secx
Odd: sinx, tanx, cotx, cscx
100
Solve the right triangle.
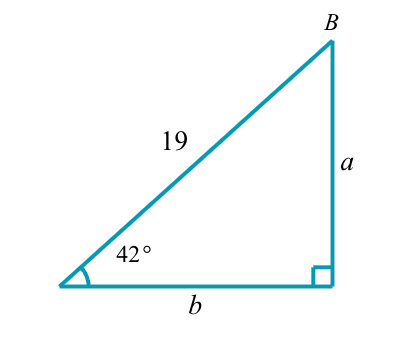
B=48o
a=12.7
b=14.1
100
What is Elizabeth's middle name?
a) Anya
b) Tai
c) Ivy
d) Rose
c) Ivy
200
Evaluate
sin((-2pi)/3)
-sqrt(3)/2
200
Determine the quadrant where secθ<0 and cotθ>0.
Quadrant III
200
Evaluate
cos(-pi/6)
using even/odd identities
sqrt(3)/2
200
Solve the right triangle.
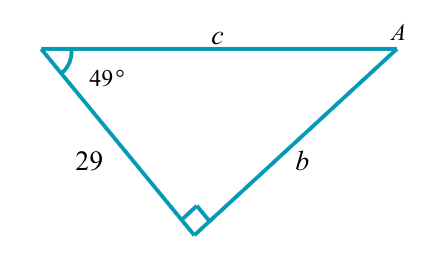
A=41o
b=33.4
c=44.2
200
When does Derzan's credit card expire?
08/28
300
Suppose that (x, 15/17) is a point in Quadrant II lying on the unit circle. Find x.
x=-8/17
300
Let θ be an angle in quadrant IV such that cosθ=4/5.
Find cscθ
cscθ=-5/3
300
Use a Pythagorean Identity to evaluate sin(β) if cos(β)=4/5 and β lies in the fourth quadrant.
sin(β)=-3/5
300
A kite is flying 94 ft off the ground, and its string is pulled taut. The angle of elevation of the kite is 52°. Find the length of the string. Round your answer to the nearest tenth.
119.3 ft
300
Which game does Junbo NOT play?
a) Minecraft
b) League of Legends
c) Monster Hunter
d) Rocket League
e) The Witcher
d) Rocket League
400
Suppose that θ is an angle in standard position whose terminal side intersects the unit circle at (5/13, -12/13).
Find cotθ
cotθ=-5/12
400
Let θ be an angle in quadrant I such that tanθ=15/8.
Find cscθ
cscθ=17/15
400
Use a Pythagorean Identity to evaluate cot(β) if sin(β)=-2/3 and β lies in the fourth quadrant.
cot(β)=-(sqrt(5))/(2)
400
Looking up, Jenny sees two hot air balloons in the sky. She determines that the lower hot air balloon is 365 meters away, at an angle of 23° from the vertical. The higher hot air balloon is 1035 meters away, at an angle of 41° from the vertical. How much higher is the one balloon from the other?
445.1 meters
400
List the SPTs youngest to oldest.
Junbo, Elizabeth, Derzan
500
Given θ=7π/6, find
tan^2θ
tan^2θ=1/3
500
Simplify the expression
(sec^2θ)/(tanθcscθ)
secθ
500
Use trig identities to simplify the expression
(1-cos^2θ)csc^2θ
1
500
Amy and Brian are standing 105m apart, and they are both looking up at a roller coaster. One of the cars of the roller coaster is moving at a constant speed of 4 m/s. The car is currently located directly above Amy, and the highest point on the roller coaster is directly above Brian. The car begins to ascend towards the highest point on the track at an angle of 32° from the horizontal. Find the remaining distance, r, that will be between the car and the highest point after 12 seconds.
75.8 meters
500
What are Derzan, Junbo, and Elizabeth's major?
*If you guess minors, you also get additional 50 points
Derzan - Computer Science
Junbo - Computer Engineers (minors: math & comp sci)
Elizabeth - Middle Childhood Education