My mom's niece is my...
cousin
A: _________ are you from?
B: I'm Japanese.
Where
you/ a house near the beach/ have got?
Have you got a house near the beach?
They are from Greece, so they are ____________.
A. Greece
B. Greecian
C. Greek
C
Martha's T-shirt is on the floor.
A. HAS
B. IS
C. POSSESSION
C

[eɪ]

[dʒiː]

[ɛks]
My cousin, Francisco, is my dad's...
nephew
A: _________ do you go camping?
B: In summer.
When / How often
she/ can jump?
Can she jump?
Dana and Sarah ______ sisters. They live next to my house.
A. IS
B. ARE
C. HAS GOT
B
Jane's 16 years old.
A. HAS
B. IS
C. POSSESSION
B

[ziː]

[kjuː]
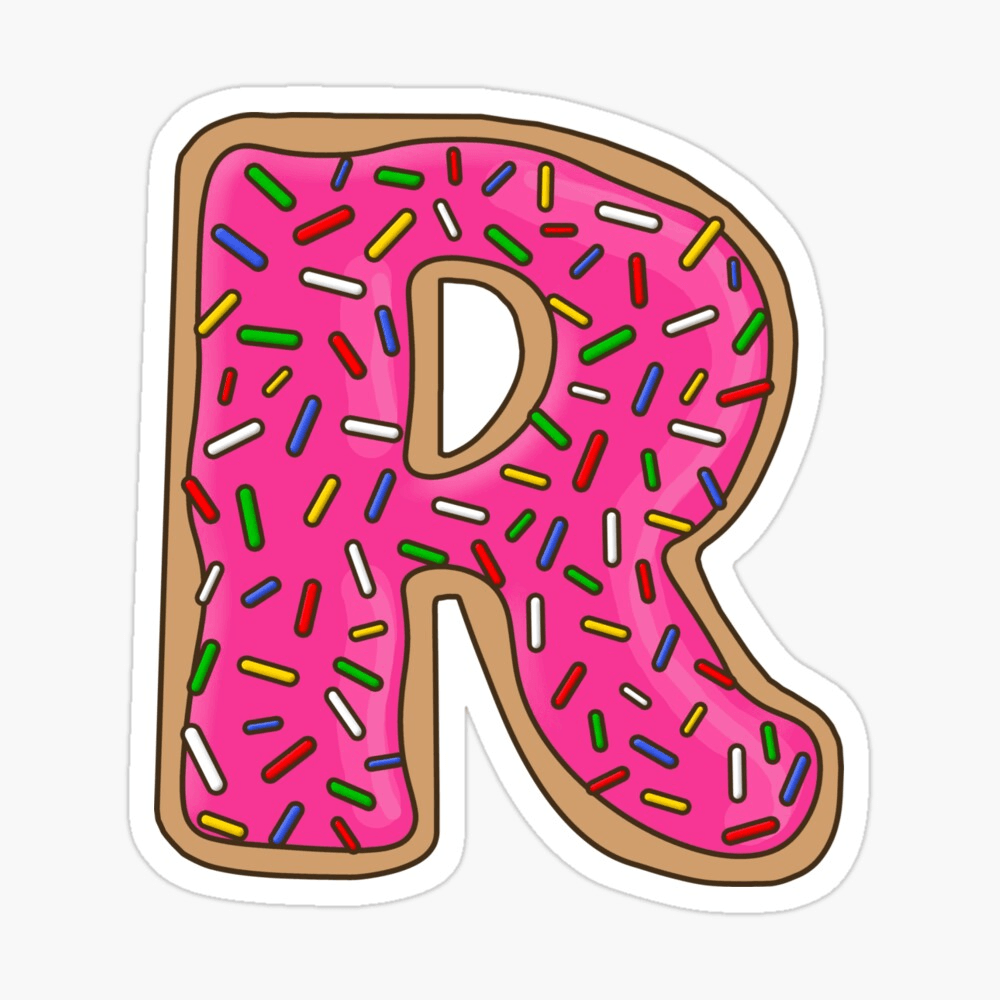
[ɑr]
Hi! I am Ainhoa. This is my grandma Graciela. I am her ...
grandchild/ granddaughter
A: _________ painted the walls?
B: My sister.
Who
Live/ in Granada/ Samuel?
Does Samuel live in Granada?
Fred: _________ sing?
Greg: Yes, I can.
A. Can you
B. You can
C. Do you can
A
He's taller than me.
A. HAS
B. IS
C. POSSESSION
B
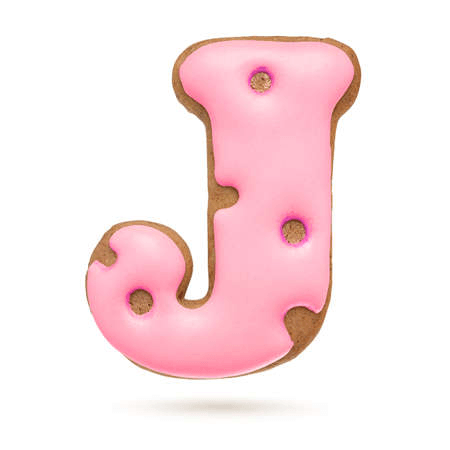
[dʒeɪ]

[iː]

[juː]
Jessica's _________ is called Ricardo. They got married 2 years ago.
husband
A: _________ comics have you got?
B: A lot.
How many
they/ like/ doing sports?
Do they like doing sports?
_________ bike is the one next to that tree.
A. Carlos
B. Carlos's
C. Carlos'
C
Lara's got a pet. It's beautiful!
A. HAS
B. IS
C. POSSESSION
Lara's: has
It's: is
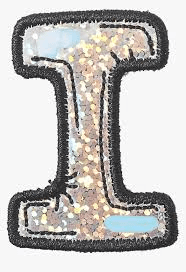
[aɪ]

[ˈdʌbəl juː]

[eɪtʃ]
My sister's daughter is my...
niece
A: ________ handbag is this?
B: It's mine.
Whose
brothers and sisters/ she/ have got/ how many?
How many brothers and sisters has she got?
Carmen__ room is very big.
A. 's
B. is
C. Both options A and B are correct
A
My sister's beautiful. She's got long hair and green eyes. She's also got a lot of friends. Her best friend's name's Anna.
A. HAS
B. IS
C. POSSESSION
sister's: is
she's got: has
she's also got: has
best friend's: possession
name's: is

[waɪ]

[keɪ]
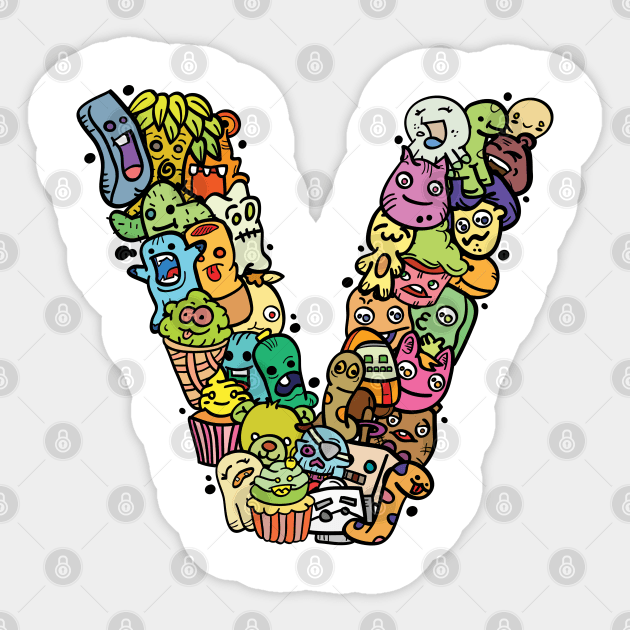
[viː]